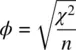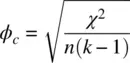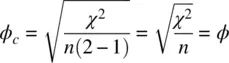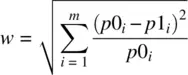The null hypothesis is that the 50 counts making up the entire table are more or less randomly distributed across each of the cells. That is, there is no association between condition and exposure. We can easily test this hypothesis in SPSS by weighting the relevant frequencies by cell total:
| exposure |
condition |
freq |
| 1.00 |
0.00 |
10.00 |
| 1.00 |
1.00 |
20.00 |
| 2.00 |
0.00 |
15.00 |
| 2.00 |
1.00 |
5.00 |
WEIGHT BY freq. CROSSTABS /TABLES=condition BY exposure /FORMAT=AVALUE TABLES /STATISTICS=CHISQ /CELLS=COUNT /COUNT ROUND CELL.
The output follows in which it is first confirmed that we set up our data file correctly:
| Exposure * Condition Crosstabulation |
| Count |
| Condition |
Total |
|
|
1.00 |
0.00 |
|
| Exposure |
1.00 |
20 |
10 |
30 |
|
2.00 |
5 |
15 |
20 |
| Total |
|
25 |
25 |
50 |
We focus on the Pearson chi‐square test value of 8.3 on a single degree of freedom. It is statistically significant ( p = 0.004), and hence we can reject the null hypothesis of no association between condition and exposure group.
| Chi‐square Tests |
|
Value |
d f |
Asymp. Sig. (two‐sided) |
Exact Sig. (two‐sided) |
Exact Sig. (one‐sided) |
| Pearson chi‐square |
8.333 a |
1 |
0.004 |
|
|
| Continuity correction b |
6.750 |
1 |
0.009 |
|
|
| Likelihood ratio |
8.630 |
1 |
0.003 |
|
|
| Fisher's exact test |
|
|
|
0.009 |
0.004 |
| Linear‐by‐linear association |
8.167 |
1 |
0.004 |
|
|
| No. of valid cases |
50 |
|
|
|
|
a 0 cells (0.0%) have expected count less than 5. The minimum expected count is 10.00.
b Computed only for a 2 × 2 table.
In R, we can easily perform the chi‐square test on this data. We first build the matrix of cell counts, calling it diag.table:
> diag.table <- matrix(c(20, 5, 10, 15), nrow = 2) > diag.table [,1] [,2] [1,] 20 10 [2,] 5 15 > chisq.test(diag.table, correct = F) Pearson's Chi-squared test data: diag.table X-squared = 8.3333, df = 1, p-value = 0.003892
We see that the result in R agrees with what we obtained in SPSS. Note that specifying correct = F(correction = false) negated what is known as Yates' correction for continuity, which involves subtracting 0.5 from positive differences in O − E and adding 0.5 to negative differences in O − E in an attempt to better make the chi‐square distribution approximate that of a multinomial distribution (i.e., in a crude sense, to help make discrete probabilities more continuous). To adjust for Yates, we can either specify correct = Tor simply chisq.test(diag.table), which will incorporate the correction. With the correction implemented, our p ‐value increases from 0.003 to 0.009 (not shown). We notice that this adjustment parallels that made in SPSS by adjusting for continuity. When expected counts per cell are relatively small (a working rule is that they should be at least five in each cell), one can also request Fisher' s exact test(see Fisher, 1922a), which we note also mirrors the output generated by SPSS:
> fisher.test(diag.table) Fisher's Exact Test for Count Data data: diag.table p-value = 0.008579 alternative hypothesis: true odds ratio is not equal to 1 95 percent confidence interval: 1.466377 26.597383 sample estimates: odds ratio 5.764989
Other useful statistics for contingency tables include the phi coefficientand Cramer's V. Phi, ϕ , is a measure of association for 2 × 2 contingency tables, computed as
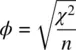
where χ 2is the chi‐square statistic calculated on the 2 × 2 table, and n is the total sample size. The maximum ϕ can attain is 1.0, indicating maximal association. ϕ can be computed in SPSS by /statistics = phiand is available in R in the psychpackage (Revelle, 2015). Cramer's ϕ cextends on ϕ in that it allows for contingency tables of greater than 2 × 2. It is included in the /statistics = phicommand and also available in R's psychpackage. It is given by:
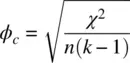
where k is the minimum of the number of rows or columns. The relationship between ϕ cand ϕ is easily shown for k = 2:
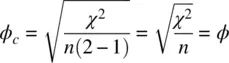
2.2.1 Power for Chi‐Square Test of Independence
We can estimate power 5 and required sample size for the chi‐square test of independence using the package pwrin R:
> library(pwr) > pwr.chisq.test (w =, N =, df =, sig.level =, power = )
where w is the anticipated or required effect size, estimated as:
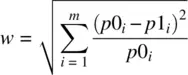
and p 0 iand p 1 iare the probabilities in a given cell i under the null and alternative hypotheses, respectively. We demonstrate by estimating power for w = 0.2:
> pwr.chisq.test(w = 0.2, N =, df = 5, sig.level = .05, power = 0.90) Chi squared power calculation w = 0.2 N = 411.7366 df = 5 sig.level = 0.05 power = 0.9 NOTE: N is the number of observations
Table 2.2 Contingency Table for 2 × 2 × 2 Design
|
Exposure |
Condition Absent (0) |
Condition Present (1) |
Total |
| Males |
Yes |
10 |
20 |
30 |
|
No |
15 |
5 |
20 |
| Females |
Yes |
13 |
17 |
30 |
|
No |
12 |
8 |
20 |
|
Total |
50 |
50 |
100 |
R estimates that a total of approximately 411 subjects are required to achieve power set at 0.90. Such a large sample is required because w = 0.2 constitutes a relatively small effect size (see Cohen (1988) for details).
The reader may ask at this point how one might go about analyzing data for higher‐dimensional frequency tables. The example for the chi‐square test of the data in Table 2.1is only for that of a 2 × 2 layout. Suppose we added a third factor to our analysis, such as gender, making our contingency table appear as in Table 2.2.
For data such as that in Table 2.2featuring higher‐dimensional frequency data, log‐linear modelsare a possibility (Agresti, 2002). Log‐linear models are an option in the wider class of generalized linear models, to be discussed further in Chapter 10, where we discuss in some detail a special case of the generalized linear model called the logistic regression model.
Читать дальше