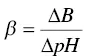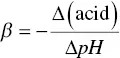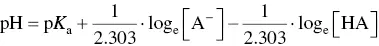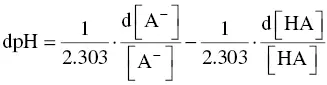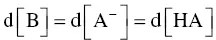Another advantage of partial elimination of malic acid over malolactic fermentation, followed by the addition of tartrate, is that, due to the low acidification rate, it does not produce wines with too low a pH. Low pH can be responsible for difficult or stuck secondary fermentation in the bottle during sparkling winemaking via the traditional method ( méthode champenoise ), leaving residual sugar in the wine.
Traditional acidification and deacidification methods are aimed solely at changing total acidity levels, with no concern for the impact on pH and even less for the buffer capacity of the wine and with all the unfortunate consequences this may have on flavor and aging potential.
This is certainly due to the lack of awareness of the importance of the acid–base buffer capacity in winemaking. Changes in the acid–base characteristics of a wine require knowledge of not only its total acidity and pH but also of its buffer capacity. These three parameters may be measured using a pH meter. Few articles in the literature deal with the buffer capacity of wine (Genevois and Ribéreau‐Gayon, 1935; Vergnes, 1940; Hochli, 1997; Dartiguenave et al ., 2000a). This lack of knowledge is probably related to the fact that buffer capacity cannot be measured directly but rather requires readings of four or five points on a neutralization curve ( Figure 1.3), and this is not one of the regular analyses carried out by winemakers.
It is now possible to automate the plotting of a neutralization curve, based on the wine's initial pH and total acidity, and thus measuring buffer capacity at the main stages in winemaking should become a routine.
Mathematically and geometrically, buffer capacity, β , and buffer range are deduced from the Henderson–Hasselbalch equation ( Section 1.4.2, Equation (1.2)). Buffer capacity is defined by Equation (1.3):
(1.3) 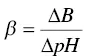
where ΔB is the number of strong base equivalents that cause an increase in pH equal to ΔpH. Buffer range is a way of assessing buffer capacity. For an organic acid alone, with its salt in solution, it may be defined as the pH interval in which the buffer effect is optimum ( Equation (1.4)):
(1.4) 
Buffer capacity is normally defined in relation to a strong base, but it could clearly be defined in the same way in relation to a strong acid. In this case, the pH = f (strong acid) function decreases, and its β differential is negative, i.e.:
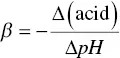
Strictly speaking, buffer capacity is obtained from the differential of the Henderson–Hasselbalch expression, i.e. from the following derived formula:
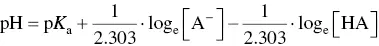
as only the Napierian logarithm is geometrically significant and provides access to the slope of the titration curve around its p K a( Figure 1.4).
The differential of the equation is as follows:
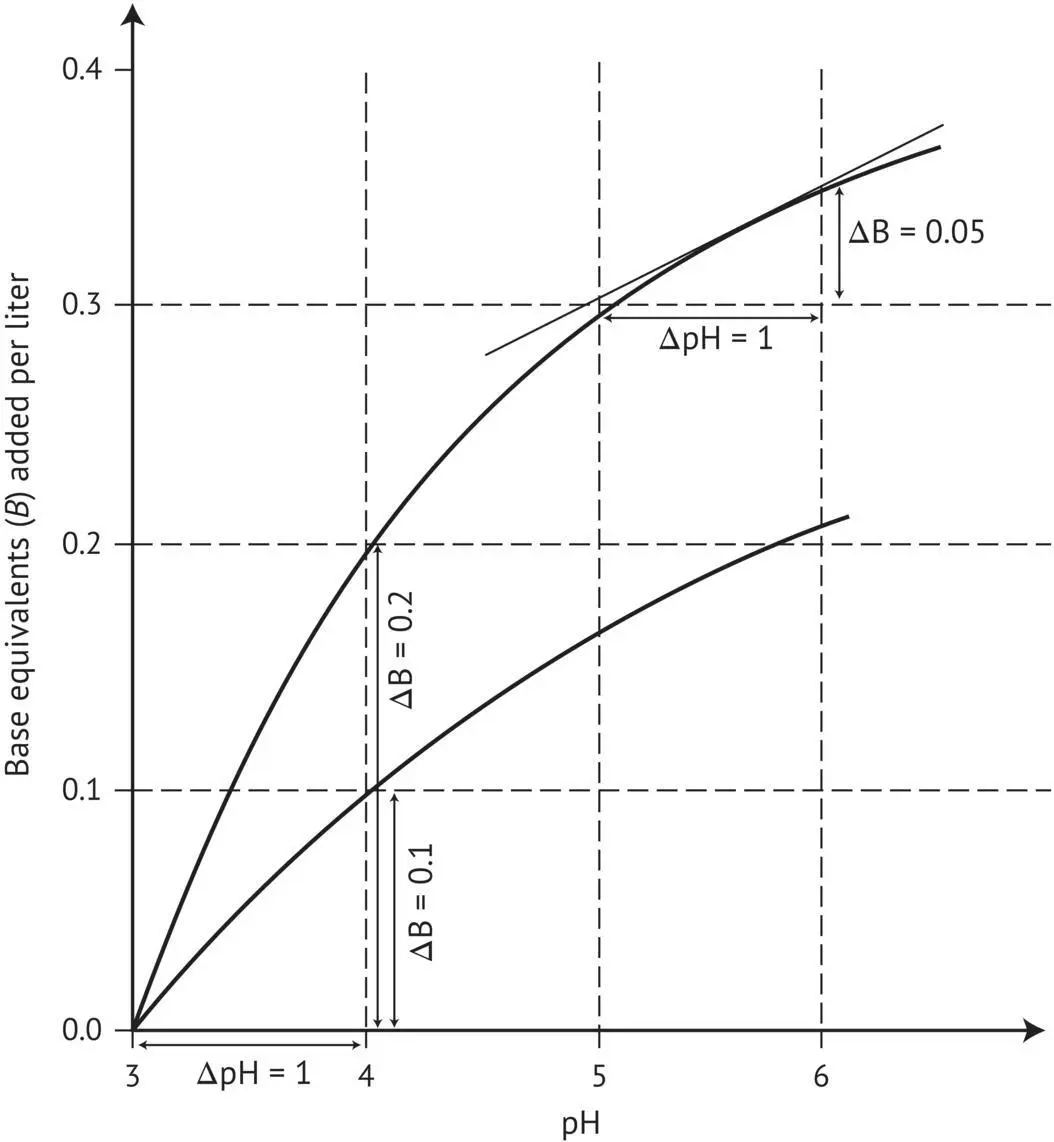
FIGURE 1.4 Determining the buffer capacity β from the titration curves of two model buffer solutions.
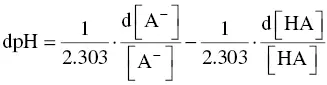
Making the assumption that the quantity of strong base added, d[B], generates the same variation in acidity in salt form, d[A −], and leads to an equal decrease in free acidity d[HA], per unit, i.e.:
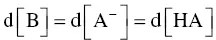
the differential equation for pH is then
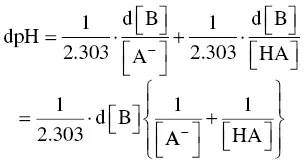
or,

Dividing both sides of the equation by d[B] gives the inverse of Equation (1.3), defining the buffer capacity. Theoretically, variations ΔB and ΔpH must be infinitely small, as the value of the ΔB/ΔpH ratio at a fixed pH corresponds geometrically to the tangent on each point on the titration curve ( Figure 1.4). More practically, buffer capacity can be defined as the number of strong base equivalents required to cause an increase in pH of 1 unit per liter of must or wine. It is even more practical to calculate smaller pH variations in much smaller samples (e.g. 30 ml). Figure 1.4clearly shows the difference in buffer capacity of a model solution between pH 3 and 4, as well as between pH 4 and 5.
This raises the issue of the pH and p K aat which buffer range should be assessed. Champagnol (1986) suggested that pH should be taken as the mean of the p K aof the organic acids in the must or wine, i.e. the mean p K aof tartaric and malic acids in must and tartaric and lactic acids in wine that has completed malolactic fermentation.
This convention is justified by its convenience, provided that ( Section 1.4.2) the neutralization curves of the must or wine have no inflection points representative of the p K aof the organic acids present, since their buffer ranges overlap, at least partially. In addition to these somewhat theoretical considerations, there are also some more practical issues. An aqueous solution of sodium hydroxide is used to determine the titration curve of a must or wine in order to measure total acidity and buffer capacity. Sodium, rather than potassium, hydroxide used as the sodium salt of tartaric acid is soluble, while potassium bitartrate would be likely to precipitate out during titration. It is, however, questionable to use the same aqueous sodium hydroxide solution for both must and for a dilute alcohol solution like wine.
Strictly speaking, a sodium hydroxide solution in dilute alcohol should be used for wine to avoid modifying the alcohol content and, consequently, the dielectric constant and, thus, the dissociation of the acids in the solution during the assay. It has been demonstrated (Dartiguenave et al ., 2000b) that the buffer capacities of organic acids, singly ( Tables 1.4and 1.5) or in binary ( Table 1.6) and tertiary ( Table 1.7) combinations, are different in water and in 11% dilute alcohol solution. However, if the solvent containing the organic acids and the sodium hydroxide is the same, there is a close linear correlation between the buffer capacity and the acid concentrations ( Table 1.4).
TABLE 1.4Equations for Calculating Buffer Capacity (mEq/l) Depending on the Concentration (mM) of the Organic Acid in Water or Dilute Alcohol Solution (11% vol.) Between 0 and 40 mM (Dartiguenave et al., 2000b)
| Solvent |
Water |
Dilute alcohol solution |
| Tartaric acid |
Y = 0.71 x + 0.29; R 2= 1 |
Y = 0.60 x + 1.33; R 2= 1 |
| Malic acid |
Y = 0.56 x + 0.43; R = 0.998 |
Y = 0.47 x + 0.33; R 2= 0.987 |
| Succinic acid |
Y = 0.56 x − 1.38 × 10 −2; R 2= 0.993 |
Y = 0.53 x + 0.52; R 2= 0.995 |
| Citric acid |
Y = 0.57 x + 0.73; R 2= 1 |
Y = 0.51 x + 0.62; R 2= 1 |
Table 1.5shows the values (mEq/l) calculated from the regression lines of the buffer capacities for acid concentrations varying from 1 to 6 g/l in water and in 11% dilute alcohol solution. The buffer capacity of each acid alone in dilute alcohol solution is lower than in water. Furthermore, the buffer capacity of a four‐carbon organic acid varies more as the number of alcohol functions increases ( Table 1.8). Thus, the variation in buffer capacity of malic acid, a diacid with one alcohol function, in a dilute alcohol medium, is 1.4 mEq/l higher than that of succinic acid. When the hydroxy acid has two alcohol functions, the increase is as high as 5.3 mEq/l (17.7%) between tartaric and malic acids, even if the buffer capacities of the three acids are lower than in water.
Читать дальше