1 1 Engel, T. and Reid, P. (2010). Physical Chemistry, 2e. Upper Saddle River, NJ: Pearson Prentice Hall.
2 2 Levine, I. (1970). Quantum Chemistry, vol. I&II. Boston: Allyn & Bacon.
3 3 Levine, I. (1983). Quantum Chemistry. Boston: Allyn & Bacon.
4 4 Kauzman, W. (1957). Quantum Chemistry. New York: Academic Press.
5 5 Eyring, H., Walter, J., and Kimball, G.E. (1967). Quantum Chemistry. New Yrok: Wiley.
6 6 Feynman, R. (1964). Probability and Uncertainty: The Quantum Mechanical View of Nature ‐ The Character of Physical Law 1964. Cornell University.
1 Transition from Classical Physics to Quantum Mechanics
At the end of the nineteenth century, classical physics had progressed to such a level that many scientists thought all problems in physical science had been solved or were about to be solved. After all, classical Newtonian mechanics was able to predict the motions of celestial bodies, electromagnetism was described by Maxwell's equations (for a review of Maxwell's equations, see [1]), the formulation of the principles of thermodynamics had led to the understanding of the interconversion of heat and work and the limitations of this interconversion, and classical optics allowed the design and construction of scientific instruments such as the telescope and the microscope, both of which had advanced the understanding of the physical world around us.
In chemistry, an experimentally derived classification of elements had been achieved (the rudimentary periodic table), although the nature of atoms and molecules and the concept of the electron's involvement in chemical reactions had not been realized. The experiments by Rutherford demonstrated that the atom consisted of very small, positively charged, and heavy nuclei that identify each element and electrons orbiting the nuclei that provided the negative charge to produce electrically neutral atoms. At this point, the question naturally arose: Why don't the electrons fall into the nucleus, given the fact that opposite electric charges do attract? A planetary‐like situation where the electrons are held in orbits by centrifugal forces was not plausible because of the (radiative) energy loss an orbiting electron would experience. This dilemma was one of the causes for the development of quantum mechanics.
In addition, there were other experimental results that could not be explained by classical physics and needed the development of new theoretical concepts, for example, the inability of classical models to reproduce the blackbody emission curve, the photoelectric effect, and the observation of spectral “lines” in the emission (or absorption) spectra of atomic hydrogen. These experimental results dated back to the first decade of the twentieth century and caused a nearly explosive reaction by theoretical physicists in the 1920s that led to the formulation of quantum mechanics. The names of these physicists – Planck, Heisenberg, Einstein, Bohr, Born, de Broglie, Dirac, Pauli, Schrödinger, and others – have become indelibly linked to new theoretical models that revolutionized physics and chemistry.
This development of quantum theory occupied hundreds of publications and letters and thousands of pages of printed material and cannot be covered here in this book. Therefore, this book presents many of the difficult theoretical derivations as mere facts, without proof or even the underlying thought processes, since the aim of the discussion in the following chapters is the application of the quantum mechanical principles to molecular spectroscopy. Thus, these discussions should be construed as a guide to twenty‐first‐century students toward acceptance of quantum mechanical principles for their work that involves molecular spectroscopy.
Before the three cornerstone experiments that ushered in quantum mechanics – Planck's blackbody emission curve, the photoelectric effect, and the observation of spectral “lines” in the hydrogen atomic spectra – will be discussed, electromagnetic radiation, or light, will be introduced at the level of a wave model of light, which was the prevalent way to look at this phenomenon before the twentieth century.
1.1 Description of Light as an Electromagnetic Wave
As mentioned above, the description of electromagnetic radiation in terms of Maxwell's equation was published in the early 1860s. The solution of these differential equations described light as a transverse wave of electric and magnetic fields. In the absence of charge and current, such a wave, propagating in vacuum in the positive z ‐direction, can be described by the following equations:
(1.1) 
(1.2) 
where the electric field 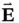 and the magnetic field
and the magnetic field 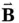 are perpendicular to each other, as shown in Figure 1.1, and oscillate in phase at the angular frequency
are perpendicular to each other, as shown in Figure 1.1, and oscillate in phase at the angular frequency
(1.3) 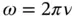
where ν is the frequency of the oscillation, measured in units of s −1= Hz. In Eqs. (1.1)and (1.2), kis the wave vector (or momentum vector) of the electromagnetic wave, defined by Eq. (1.4):
(1.4) 
Here, λ is the wavelength of the radiation, measured in units of length, and is defined by the distance between two consecutive peaks (or troughs) of the electric or magnetic fields. Vector quantities, such as the electric and magnetic fields, are indicated by an arrow over the symbol or by bold typeface.
Since light is a wave, it exhibits properties such as constructive and destructive interference. Thus, when light impinges on a narrow slit, it shows a diffraction pattern similar to that of a plain water wave that falls on a barrier with a narrow aperture. These wave properties of light were well known, and therefore, light was considered to exhibit wave properties only, as predicted by Maxwell's equation.
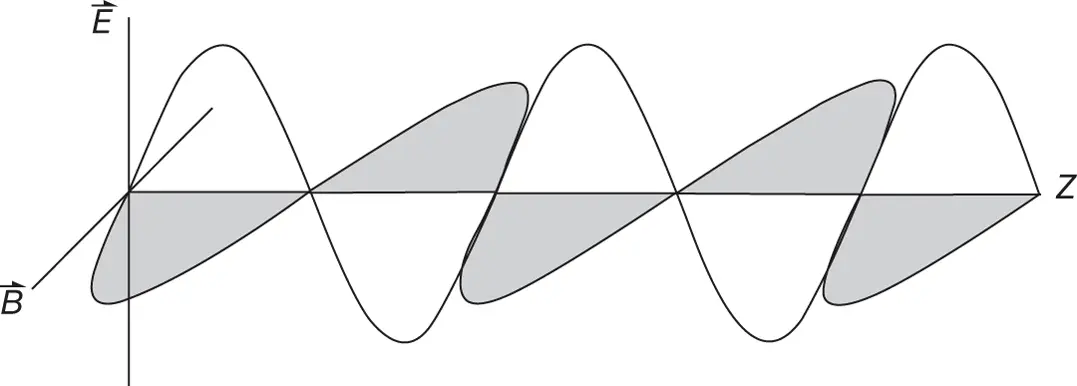
Figure 1.1 Description of the propagation of a linearly polarized electromagnetic wave as oscillation of electric ( 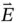 ) and magnetic (
) and magnetic ( 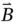 ) fields.
) fields.
In general, any wave motion can be characterized by its wavelength λ , its frequency ν, and its propagation speed. For light in vacuum, this propagation speed is the velocity of light c ( c = 2.998 × 10 8m/s). (For a list of constants used and their numeric value, see Appendix 1.) In the context of the discussion in the following chapters, the interaction of light with matter will be described as the force exerted by the electric field on the charged particles, atoms, and molecules (see Chapter 3). This interaction causes a translation of charge. This description leads to the concept of the “electric transition moment,” which will be used as the basic quantity to describe the likelihood (that is, the intensity) of spectral transition.
Читать дальше



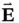 and the magnetic field
and the magnetic field 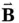 are perpendicular to each other, as shown in Figure 1.1, and oscillate in phase at the angular frequency
are perpendicular to each other, as shown in Figure 1.1, and oscillate in phase at the angular frequency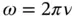


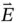 ) and magnetic (
) and magnetic ( 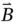 ) fields.
) fields.










