From the latter point of view, introducing probability measure spaces and random‐variables‐as‐measurable‐functions seems to be an unnecessary complication. So, from such a straightforward starting point, why does the theory become so challenging and “messy”, as portrayed in Chapter 1
As in Example 2, the illustration in Section 2.3involves dividing up the time period (4 days) into 4 sections; leading to sample space 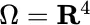 in ( 2.15). Why not simply continue in this vein, and subdivide the time into 40, or 400, or 4 million steps instead of just 4; using sample spaces
in ( 2.15). Why not simply continue in this vein, and subdivide the time into 40, or 400, or 4 million steps instead of just 4; using sample spaces 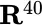 , or
, or 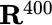 , or
, or 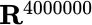 , respectively? The computations may become lengthier, but no new principle is involved; each of the variables changes in discrete steps at discrete points in time. 5
, respectively? The computations may become lengthier, but no new principle is involved; each of the variables changes in discrete steps at discrete points in time. 5
Other simplifications can be similarly adopted. For instance, only two kinds of changes are contemplated in Section 2.3: increase (Up) or decrease (Down). But that is merely a slight technical limitation. Just as the number of discrete times can be increased indefinitely, so can the number of distinct, discrete values which can be potentially taken at any instant.
There is a plausible argument for this essentially discrete approach, at least in the case of financial shareholding. Actual stock market values register changes at discrete intervals of time (time ticks), and the amount of change that can occur is measured in discrete divisions (or basis points) of the currency.
So why does the mathematical model for such processes (as described in Chapter 1, for instance) require passages to a limit involving infinite divisibility of both the time domain, and the value range?
In fact there are sound mathematical reasons for this seemingly complicated approach. For one thing, instead of choosing one of many possible finite division points of time and values, passage to a limit—if that is possible—replaces a multiplicity of rather arbitrary choices by a single definite procedure, which may actually be easier to compute.
Furthermore, Brownian motion provides a good mathematical model for many random processes, and Brownian motion is based on continuous time and continuous values, not discrete.
The finite sum calculation 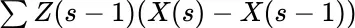 is a good enough starting point for stochastic integration. But it is only a starting point. The question is, by successive sub‐division of time and/or values, can a single limiting result be found—a single random variable to replace all those obtained, as in Section 2.3, by computation with discrete times/values? In other words, is there convergence to a limit?
is a good enough starting point for stochastic integration. But it is only a starting point. The question is, by successive sub‐division of time and/or values, can a single limiting result be found—a single random variable to replace all those obtained, as in Section 2.3, by computation with discrete times/values? In other words, is there convergence to a limit?
The account in I1, I2, I3, I4of Chapter 1suggests that stochastic integrals converge, not in the strict sense of convergence, but only in some loose or weak manner. Our aim is to shed more light on the nature of convergence that appears in these constructions.
There is a more fundamental and compelling reason for introducing sophisticated measure theory into probability. Accessing the full power of probability, beyond the elementary calculations of Sections 2.3and 2.4, requires an understanding of the operation, scope and limitations of results such as the Laws of Large Numbers, and the Central Limit Theorems of probability theory. This increased power was eventually achieved in the early twentieth century by A.N. Kolmogorov [93] and others, who formulated the theory of probability in terms of probability measure spaces; so random variables were understood, not as potential outcome data in association with their linked probabilities (as in Sections 2.3and 2.4), but as measurable functions mapping an abstract probability space or sample space into a set of potential outcome data; thereby imposing a probability structure on the actual data.
The new power which Kolmogorov's innovation added to our understanding of probability springs from his interpretation of probability and expected value in terms of, respectively, measure theory and Lebesgue integral. The specific feature of the Lebesgue integral which enables this improvement is its enhanced convergence properties.
Earlier versions of integration—examples being the “integral as anti‐derivative”, and the Riemann integral (see Chapter 10)—did not provide adequate rationale for integrability of the limit of a convergent sequence of integrable functions. Lebesgue integration, on the other hand, has a dominated convergence theorem: if the absolute value of each member of a convergent sequence of integrable functions is less than some integrable function, then the limit function of the sequence of functions is integrable.
Introducing Lebesgue integration (and its dominated convergence theorem) into probability theory brought about the twentieth century's great advances in our understanding of random variation, including Brownian motion and stochastic integration. The price paid for this included the somewhat counter‐intuitive and challenging notion that a random variable, such as a stochastic integral, is to be thought of as a measurable function.
But the unchallenging and intuitive finite sums of ( 2.6) look remarkably like Riemann sums. (This point is elaborated in [MTRV] pages 15–17.) What if Riemann integration can be adjusted so that it incorporates (for instance) a dominated convergence theorem?
A theory of probability on these lines is presented in [MTRV]. The purpose of Part I of this book is to examine some features of this Riemannian version of probability theory, particularly in relation to stochastic integration.
Similarly Part II investigates the Riemann approach to problems of path integration in quantum mechanics.
1 1 In fact is a finite family so there are only finitely many cases to check for additivity.
2 2 [MTRV] also deals with complex‐valued random variables. Also, in the classical definition of the Itô integral (I1, I2, I3, I4 above) the integrands are measurable functions whose values are random variables (so the values are functions rather than numbers).
3 3 A Stieltjes integral is “the integral of a point function with respect to a point function ”, . See section 1.4 of [MTRV], pages 7–14.
4 4 In accordance with the presentation in [MTRV], notation (square brackets) is used with random variables (conceived “naively” or “realistically” as potential data, along with their probabilities), while round brackets are used when random variables are interpreted as ‐measurable functions .
5 5 R. Feynman proposed something on those lines to deal with an analogous problem in the path integral theory of quantum mechanics. See his comments on “subdivision and limiting processes” quoted in page 17 above.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Читать дальше

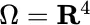 in ( 2.15). Why not simply continue in this vein, and subdivide the time into 40, or 400, or 4 million steps instead of just 4; using sample spaces
in ( 2.15). Why not simply continue in this vein, and subdivide the time into 40, or 400, or 4 million steps instead of just 4; using sample spaces 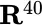 , or
, or 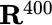 , or
, or 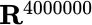 , respectively? The computations may become lengthier, but no new principle is involved; each of the variables changes in discrete steps at discrete points in time. 5
, respectively? The computations may become lengthier, but no new principle is involved; each of the variables changes in discrete steps at discrete points in time. 5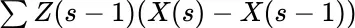 is a good enough starting point for stochastic integration. But it is only a starting point. The question is, by successive sub‐division of time and/or values, can a single limiting result be found—a single random variable to replace all those obtained, as in Section 2.3, by computation with discrete times/values? In other words, is there convergence to a limit?
is a good enough starting point for stochastic integration. But it is only a starting point. The question is, by successive sub‐division of time and/or values, can a single limiting result be found—a single random variable to replace all those obtained, as in Section 2.3, by computation with discrete times/values? In other words, is there convergence to a limit?










