Patrick Muldowney - Gauge Integral Structures for Stochastic Calculus and Quantum Electrodynamics
Здесь есть возможность читать онлайн «Patrick Muldowney - Gauge Integral Structures for Stochastic Calculus and Quantum Electrodynamics» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Gauge Integral Structures for Stochastic Calculus and Quantum Electrodynamics
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Gauge Integral Structures for Stochastic Calculus and Quantum Electrodynamics: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Gauge Integral Structures for Stochastic Calculus and Quantum Electrodynamics»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
, left off,
introduces readers to particular problems of integration in the probability-like theory of quantum mechanics. Written as a motivational explanation of the key points of the underlying mathematical theory, and including ample illustrations of the calculus, this book relies heavily on the mathematical theory set out in the author’s previous work. That said, this work stands alone and does not require a reading of
in order to be understandable.
Gauge Integral Structures for Stochastic Calculus and Quantum Electrodynamics Stochastic calculus, including discussions of random variation, integration and probability, and stochastic processes. Field theory, including discussions of gauges for product spaces and quantum electrodynamics. Robust and thorough appendices, examples, illustrations, and introductions for each of the concepts discussed within. An introduction to basic gauge integral theory. The methods employed in this book show, for instance, that it is no longer necessary to resort to unreliable «Black Box» theory in financial calculus; that full mathematical rigor can now be combined with clarity and simplicity. Perfect for students and academics with even a passing interest in the application of the gauge integral technique pioneered by R. Henstock and J. Kurzweil,
is an illuminating and insightful exploration of the complex mathematical topics contained within.

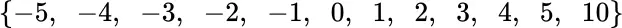
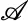 was the family of all subsets of
was the family of all subsets of  , and the example was illustrated by means of two distinct probability measures
, and the example was illustrated by means of two distinct probability measures 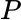 , one of which was based on Up and Down transitions being equally likely, where for the other measure an Up transition was twice as likely as a Down.
, one of which was based on Up and Down transitions being equally likely, where for the other measure an Up transition was twice as likely as a Down.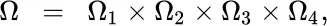
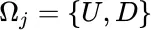 for
for 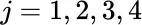 ; so the elements
; so the elements 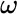 of
of  consist of sixteen 4‐tuples of the form
consist of sixteen 4‐tuples of the form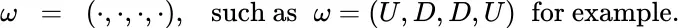
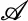 be the family of all subsets
be the family of all subsets 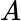 of
of  ; so
; so 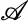 contains
contains 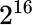 members, one of which (for example) is
members, one of which (for example) is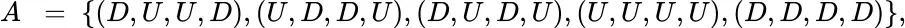
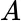 consisting of five individual four‐tuples. Assume that Up transitions and Down transitions are equally likely, and that they are independent events. Then, as before,
consisting of five individual four‐tuples. Assume that Up transitions and Down transitions are equally likely, and that they are independent events. Then, as before,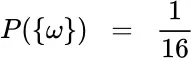
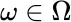 . For
. For 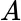 above,
above, 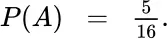
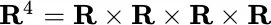 , and let
, and let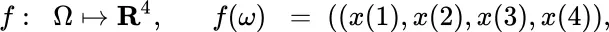
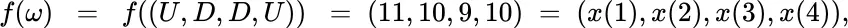
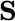 denote the stochastic integrals of the preceding section, so for
denote the stochastic integrals of the preceding section, so for 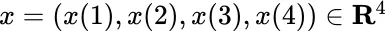 ,
,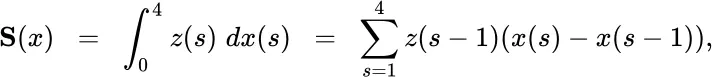
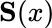 gives the values
gives the values 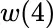 of Table 2.4. As described in Section 2.3, the rationale for deducing the probabilities of outcomes
of Table 2.4. As described in Section 2.3, the rationale for deducing the probabilities of outcomes 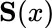 ,
, 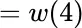 , from the probabilities on
, from the probabilities on  is the relationship
is the relationship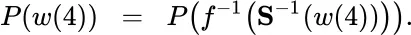
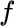 and
and 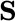 ) must be measurable. But that is no problem in this case since all the sets involved are finite. To illustrate the calculation, take
) must be measurable. But that is no problem in this case since all the sets involved are finite. To illustrate the calculation, take 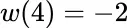 . Then, referring to Table 2.4whenever necessary,
. Then, referring to Table 2.4whenever necessary,










