(5.5.20) 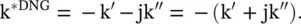
The complex DPS medium is also described by the complex refractive index:
(5.5.21) 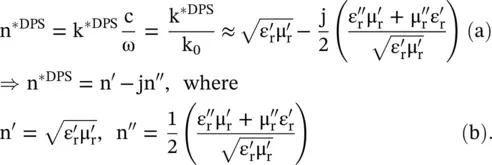
However, in the case of a complex DNG medium, the complex refractive index is n *DNG= − (n′ + jn″); as Re(n *DNG) is a negative quantity and Im(n *DNG) is still a positive quantity. The above discussion is for the propagating waves in the DPS and DNG media. However, in case the waves are nonpropagating ( evanescent ) in both media, the real part of the wavenumber is an imaginary quantity i.e. k′ = − jα′. The evanescent wave behaves differently in the DPS and DNG media. It is examined below.
The electric fields of the x‐directed propagating and nonpropagating EM‐waves in the unbounded lossy DPS and DNG media could be expressed as follows:
(5.5.22) 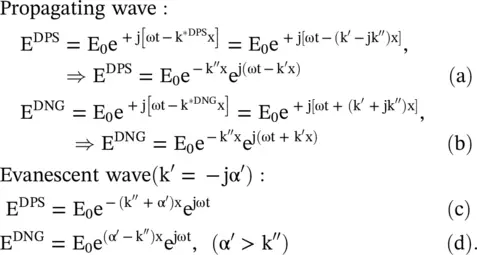
The propagating EM‐wave is attenuated while traveling in both the DPS and DNG lossy media k ″≠ 0. However, the DPS medium offers a lagging phase , whereas the DNG medium offers a leading phase to the wave traveling in the positive x‐direction. Poynting vector decides the direction of the EM‐wave propagation. The λ g/2‐line resonator could be designed in the DPS‐DNG composite, with a length λ g/4 in each medium, without any phase‐shift at the output. The classical λ g/2‐line resonator, in a DPS medium, has 180° phase at the output. It is further seen from the above equation that the evanescent wave is decaying with distance x while traveling in the DPS medium. The enhancement of amplitude by the DNG medium could be viewed as the step‐up transformer action, whereas it is increasing in amplitude while traveling in the DNG medium. This property is more clearly seen in a lossless medium with k ″= 0.
5.5.5 Wave Propagation in DNG Slab
The EM‐wave propagating through a normal DPS slab provides the lagging phase of the propagating part of the field at the output end of the slab. It is noted that the nonpropagating decaying evanescent wave also exists, along with the propagating wavefield components, inside the slab. However, for a propagating wave, the DNG slab provides the leading phase at its output. The increasing evanescent wave exists inside a DNG slab, along with the propagating wavefield components. Thus, the DNG slab can act both as (i) a phase‐compensator and (ii) as an amplitude‐compensator , i.e. as a field amplifier , without any power amplification. The field amplifier is like a voltage step‐up transformer without any power amplification. The first property, in the form of the DGS‐DNG composite slab, is helpful in the design of compact sub‐wavelength resonator [J.12, B.6]. A normal DPS resonator is half‐wavelength long. The second property offers an opportunity to design subwavelength resolution superlens [J.2, J.13–J.21]. This subsection explains both properties of a DNG slab. The superlens is discussed briefly in the next subsection.
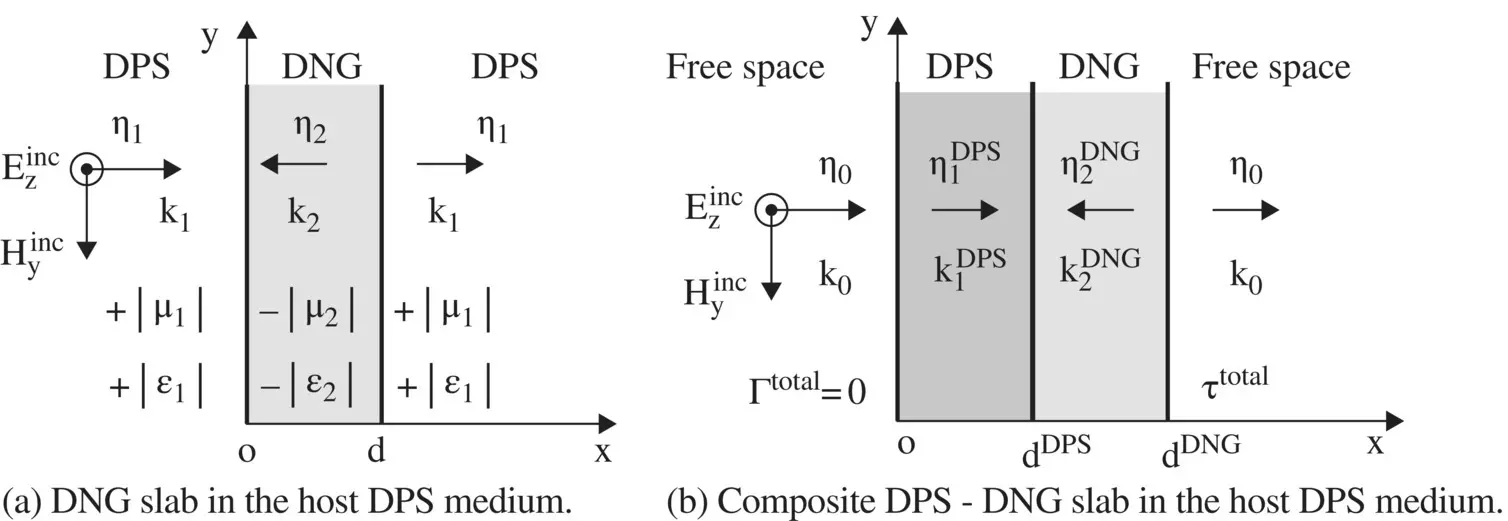
Figure 5.11 EM‐wave propagation through the DNG and composite DPS‐DNG slabs.
Phase – Compensation in the DPS‐DNG Slab
Figure (5.11a)shows a DNG slab, μ 2= − |μ 2|, ε 2= − |ε 2|, η 2, of thickness d embedded in the DPS host medium, μ 1= + |μ 1|, ε 1= + |ε 1|, η 1. The TE‐polarized wave is normally incident at the first interface. The DNG slab supports the backward wave with the wavevector k 2in the opposite direction, as power flows from the left to right. This has important consequences.
Let us assume that in Fig (5.11a), the slab is a DPS type, and it is impedance matched with the host DPS medium, i.e. η 1= η 2. The reflection and transmission coefficients are obtained from equation (5.4.15):
(5.5.23) 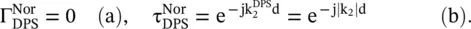
However, if the DPS slab is replaced by a matched DNG slab, then the following expressions are obtained, on using 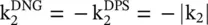 from equation (5.5.6b):
from equation (5.5.6b):
(5.5.24) 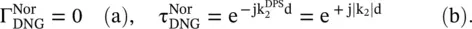
A complete transmission of waves occurs through the DPS/DNG slab. However, the DPS slab provides the lagging phase (ϕ = − |k 2|d) at the output of the slab, whereas the DNG slab provides the leading phase (ϕ = + |k 2|d). This property of the DNG slab is useful in compensating the lagging phase of a DPS slab in a DPS‐DNG composite slab.
Figure (5.11b)of the composite DPS‐DNG slab illustrates the application of a DNG slab as a phase compensator . Again, the impedance matching of both slabs with the host medium is assumed, i.e. η 1= η 2= η 0, such that the total reflection coefficient is zero,  . The total transmission coefficient at the out of the DNG slab is given as follows:
. The total transmission coefficient at the out of the DNG slab is given as follows:
(5.5.25) 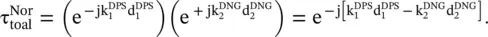
To get the compensated phase, i.e. the zero phase, at the output of the DPS‐DNG slab, the following condition, obtained from the above equation, must be met:
(5.5.26) 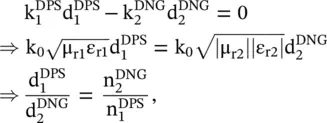
where 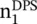 and
and 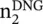 are refractive indices of the DPS and DNG slabs. The thicknesses of the slabs need not be equal. The dimension of thicknesses could be even in the sub‐wavelength. It is useful in designing of very compact sub‐wavelength cavity resonators and parallel plate waveguides [J.12]. Such resonance can be developed even in the compact composite ENG‐MNG slab [B.6]. The present concept also finds application in designing properly matched electrically small dipole antenna [B.6].
are refractive indices of the DPS and DNG slabs. The thicknesses of the slabs need not be equal. The dimension of thicknesses could be even in the sub‐wavelength. It is useful in designing of very compact sub‐wavelength cavity resonators and parallel plate waveguides [J.12]. Such resonance can be developed even in the compact composite ENG‐MNG slab [B.6]. The present concept also finds application in designing properly matched electrically small dipole antenna [B.6].
Amplitude‐Compensation in the DNG Slab
The resolving power of an optical lens is restricted by the wavelength of a source. This is known as the diffraction limit of the lens. Fourier optics, i.e. the wave optics adequately explain it in terms of the propagating waves and decaying evanescent waves generated by the object source shown in Fig (5.12a). The object source located at x = 0 generates an arbitrary wave field that can be decomposed in terms of the plane wave spectrum. Their superposition reconstructs the wave field. Thus, the wavefield in the real DPS space, propagating in the x‐direction, is composed of 2D Fourier plane wave components in the Fourier domain, i.e. in the k‐space ( propagation vector space ). The wave field 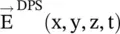 is expressed through the following 2D Fourier integral:
is expressed through the following 2D Fourier integral:
Читать дальше

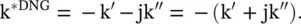
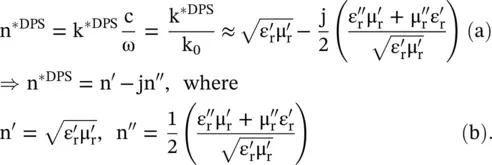
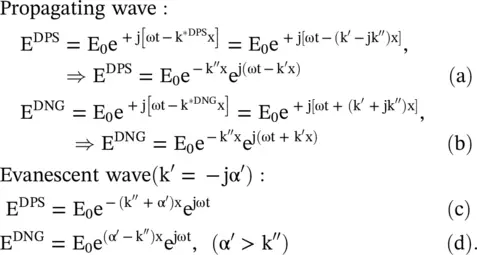

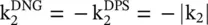 from equation (5.5.6b):
from equation (5.5.6b):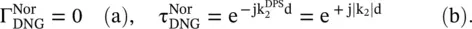
 . The total transmission coefficient at the out of the DNG slab is given as follows:
. The total transmission coefficient at the out of the DNG slab is given as follows: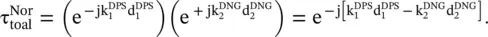
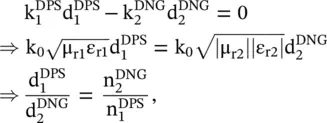
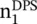 and
and 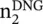 are refractive indices of the DPS and DNG slabs. The thicknesses of the slabs need not be equal. The dimension of thicknesses could be even in the sub‐wavelength. It is useful in designing of very compact sub‐wavelength cavity resonators and parallel plate waveguides [J.12]. Such resonance can be developed even in the compact composite ENG‐MNG slab [B.6]. The present concept also finds application in designing properly matched electrically small dipole antenna [B.6].
are refractive indices of the DPS and DNG slabs. The thicknesses of the slabs need not be equal. The dimension of thicknesses could be even in the sub‐wavelength. It is useful in designing of very compact sub‐wavelength cavity resonators and parallel plate waveguides [J.12]. Such resonance can be developed even in the compact composite ENG‐MNG slab [B.6]. The present concept also finds application in designing properly matched electrically small dipole antenna [B.6].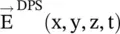 is expressed through the following 2D Fourier integral:
is expressed through the following 2D Fourier integral:










