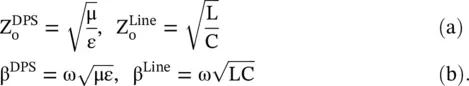The evaluation of the square root of negative permeability and negative permittivity is a critical issue in the DNG medium. The negative number (−1) is exp(±jπ). However, to meet the physical condition, discussed in sub section (5.5.3), we take {−1 = exp(−jπ)} [J.8, J.9]. Therefore, the square roots of negative permeability and negative permittivity are obtained as follows:
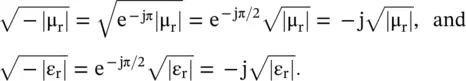
Using the above relations, the refractive index of a DNG medium, and also the propagation constant, are obtained as follows:
(5.5.6) 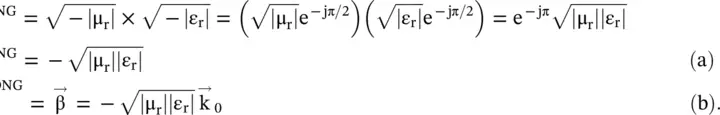
It is interesting to note that the refractive index for a DPS medium n DPSis a positive quantity, whereas for a DNG medium n DNGis a negative quantity. So the metamaterials are also known as the negative refractive index materials , i.e. the NIM . Snell's law of refraction for a DNG medium is also modified accordingly. The negative refractive index also shows the reversal of the direction of the phase velocity of the EM‐wave. However, first let us discuss the intrinsic impedance, i.e. the wave impedance for the DNG and SNG media.
Wave Impedance of DNG and SNG Media
Following equation ( 4.5.26b)of chapter 4, the wave impedance η DNGin a DNG medium is written below:
(5.5.7) 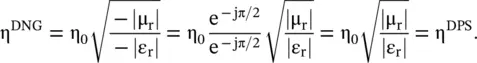
Like the wave impedance in a DPS medium η DPS, the wave impedance in the DNG medium η DNGis a positive quantity; showing the outward power flow from the source into a DNG medium. However, the wave impedances of the ENG and MNG media are reactive due to nonpropagating evanescent mode:
(5.5.8) 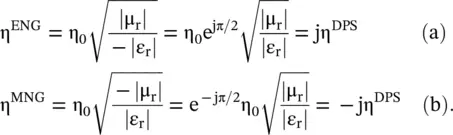
The inductive/capacitive reactive wave impedances of the ENG and MNG media create the reflecting surfaces . The circuit model of the metamaterials, discussed in section (5.5.3), elaborates on the nature of the RIS. Further details of the artificial RIS surface is discussed in section (20.2) of chapter 20. It is noted that the ENG/MNG medium is realized through the nonpropagating evanescent wave. Such an environment is provided by a rectangular waveguide below the cut‐off region. It is commented in subsection (7.4.1) of chapter 7.
The propagation constants of EM‐waves in the ENG and MNG media are obtained below:
(5.5.9) 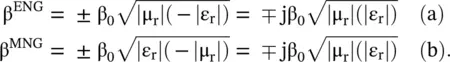
Expressions (5.5.9 a,b)show that the ENG and MNG media do not support wave propagation. Figure (5.7)shows that these media are placed in the second and fourth quadrants in the (μ r, ε r)‐plane. They only support the decaying evanescent mode.
Negative Refraction in DPS‐DNG Composite Medium
Figure (5.9a)shows the DPS‐DNG composite medium. The incident ray is in the third quadrant of the DPS medium #1. For the DPS medium #2, the refracted ray comes out in the first quadrant; as the angle of refraction (θ 2) is positive. The refraction in the DPS‐DPS composite medium follows Snell's law given by equation (5.2.7c). However, if the medium #2 is DNG‐type then the angle of refraction (−θ 2) is negative due to the negative refractive index. It follows from Snell's law:
(5.5.10) 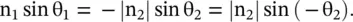
Figure (5.9a)shows that due to the negative angle of refraction (−θ 2), the refracted ray in the DNG medium #2 emerges from the fourth quadrant. It shows the reversal of Snell's law in the DPS‐DNG composite medium, as compared to Snell's law in the DPS‐DPS composite medium. Figure (5.9b)shows that the wavevector  in medium #2 must be in the reverse direction to meet the phase‐matching condition,
in medium #2 must be in the reverse direction to meet the phase‐matching condition, 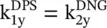 , at the interface of the composite medium.
, at the interface of the composite medium.
In the case of the TE‐polarized incident waves, the wavevectors of the incident, reflected, and refracted rays are given by equations ( 5.2.1a–d), whereas their Poynting vectors are given in equations ( 5.2.5a–c). For the DPS‐DPS composite medium, both vectors are in the same direction after refraction, showing the presence of the forward‐wave in medium #2. However, for the DPS‐DNG medium, these vectors of the transmitted wave in the DNG medium #2 are given as
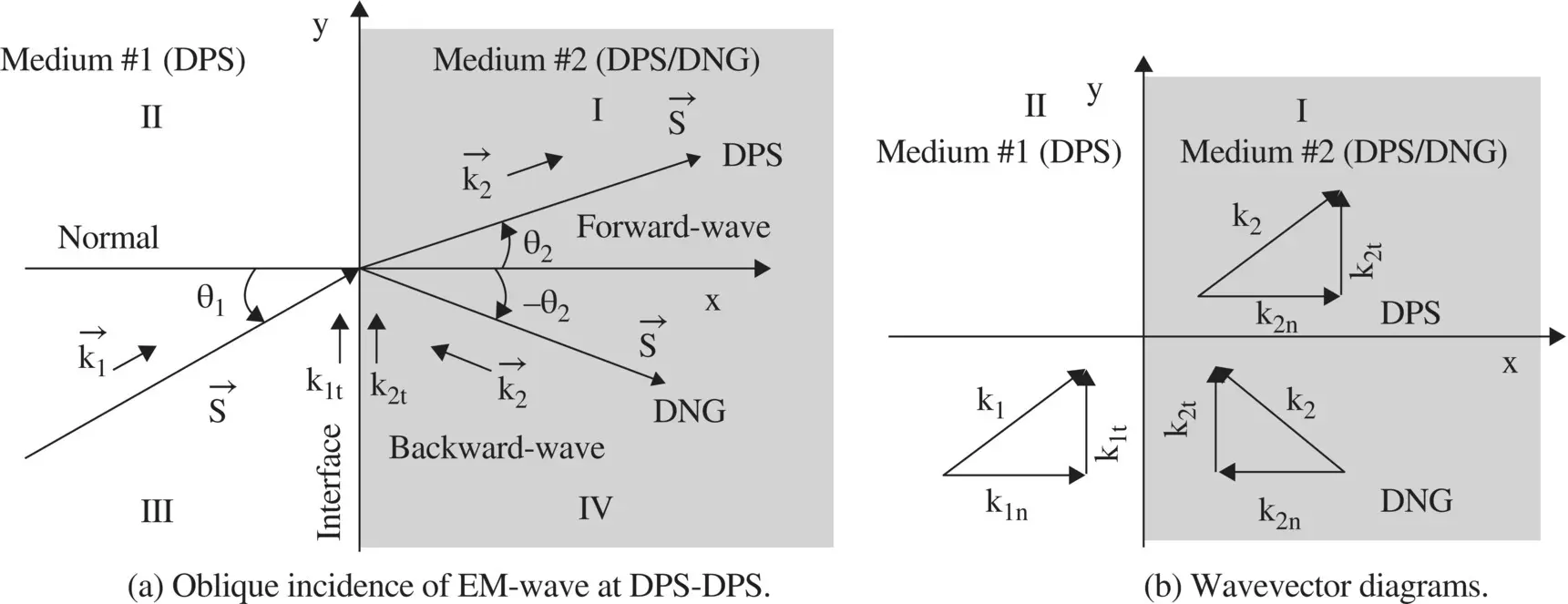
Figure 5.9 Refraction of the obliquely incident EM‐wave at the interface of the DPS‐DPS and DPS‐DNG composite medium.
(5.5.11) 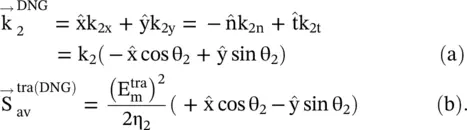
The wavevector 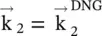 , satisfying the phase‐matching at the interface, of the above expressions, is obtained from Fig (5.9b). The Poynting vector is written from the wavevector diagram shown in Fig (5.9a). It is also obtained by using equation (5.2.4)to compute the Poynting vector in the DNG medium for the angle of refraction (−θ 2). The above expressions further show that the DNG medium #2 supports the backward‐wave propagation because the vectors
, satisfying the phase‐matching at the interface, of the above expressions, is obtained from Fig (5.9b). The Poynting vector is written from the wavevector diagram shown in Fig (5.9a). It is also obtained by using equation (5.2.4)to compute the Poynting vector in the DNG medium for the angle of refraction (−θ 2). The above expressions further show that the DNG medium #2 supports the backward‐wave propagation because the vectors 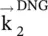 and
and 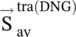 are anti‐parallel.
are anti‐parallel.
5.5.3 Basic Transmission Line Model of the DNG Medium
The unbounded DPS medium and a transmission line both support the forward wave propagation in the TEM mode, so Fig ( 3.28a)of chapter 3models a DPS medium by the LC transmission line. The equivalence between the material parameters ε, μ and the circuit parameters C, L is discussed in subsection ( 3.4.2) of chapter 3. The characteristics impedance and propagation constant of the DPS medium and equivalent transmission lines are summarized below:
(5.5.12) 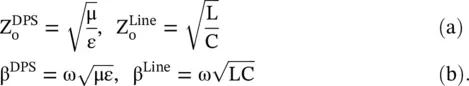
Читать дальше

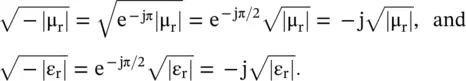
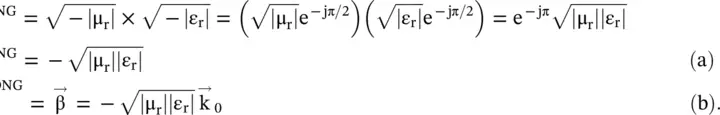
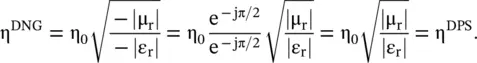
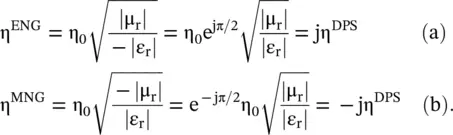
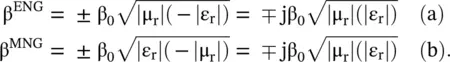
 in medium #2 must be in the reverse direction to meet the phase‐matching condition,
in medium #2 must be in the reverse direction to meet the phase‐matching condition,  , at the interface of the composite medium.
, at the interface of the composite medium.
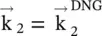 , satisfying the phase‐matching at the interface, of the above expressions, is obtained from Fig (5.9b). The Poynting vector is written from the wavevector diagram shown in Fig (5.9a). It is also obtained by using equation (5.2.4)to compute the Poynting vector in the DNG medium for the angle of refraction (−θ 2). The above expressions further show that the DNG medium #2 supports the backward‐wave propagation because the vectors
, satisfying the phase‐matching at the interface, of the above expressions, is obtained from Fig (5.9b). The Poynting vector is written from the wavevector diagram shown in Fig (5.9a). It is also obtained by using equation (5.2.4)to compute the Poynting vector in the DNG medium for the angle of refraction (−θ 2). The above expressions further show that the DNG medium #2 supports the backward‐wave propagation because the vectors 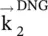 and
and 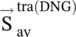 are anti‐parallel.
are anti‐parallel.