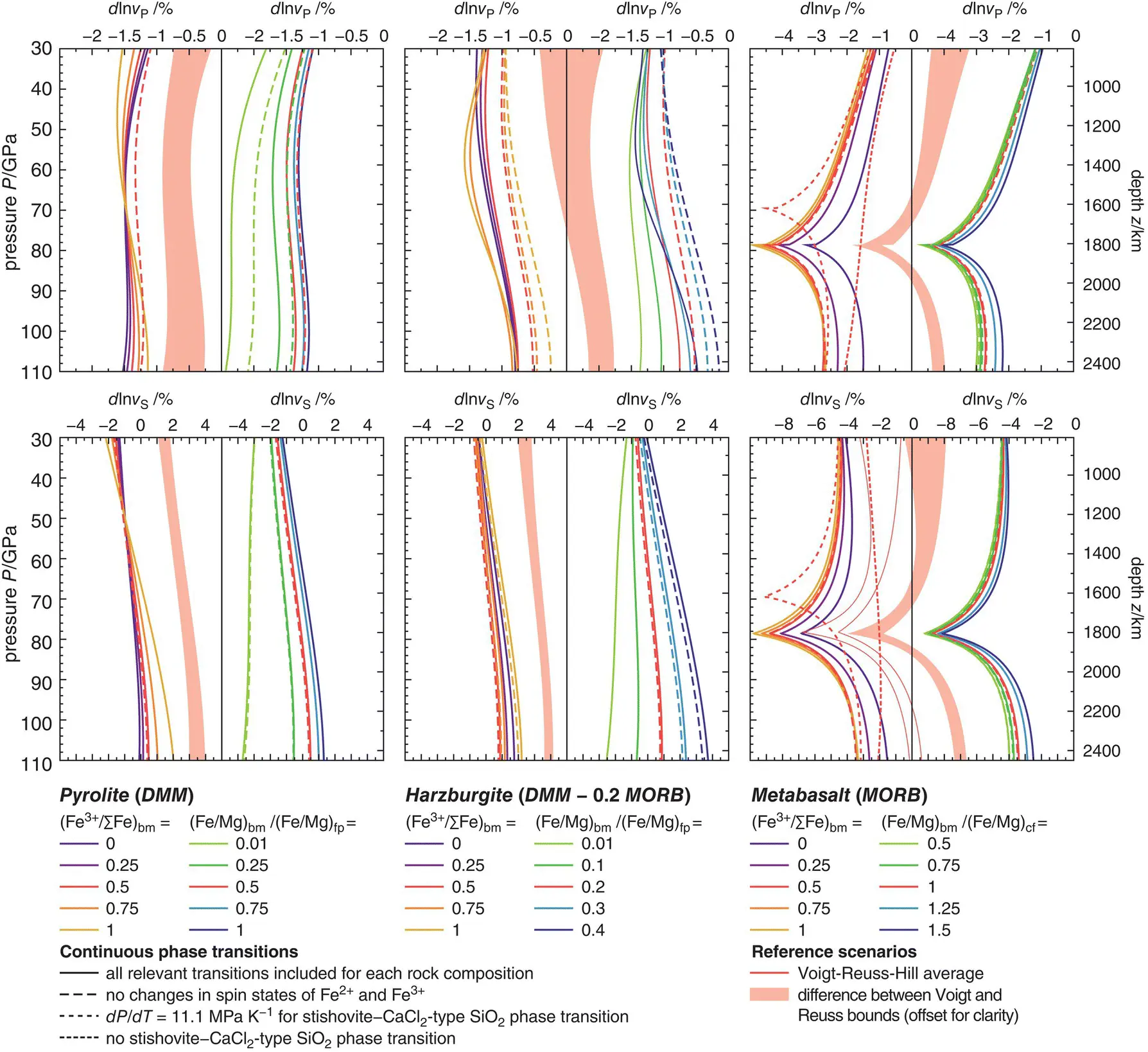
Figure 3.9 Relative contrasts between modeled P -wave (upper row) and S -wave (lower row) velocities for pyrolitic (left column), harzburgitic (central column), and basaltic (right column) bulk rock compositions and PREM along adiabatic compression paths starting at 1900 K and 25 GPa (see Figure 3.8). Variations in the Fe 3+/∑Fe ratio of bridgmanite and in the Fe‐Mg exchange coefficient have been explored for each bulk rock composition as indicated below the respective diagrams. Dashed curves show P‐ and S‐ wave velocity contrasts when the effect of different continuous phase transitions on elastic properties is ignored or modified as specified. Red shaded bands indicate the differences in modeled P‐ and S‐ wave velocity contrasts that result from combining the elastic properties of mineral phases and compositions according to either the Voigt or the Reuss bound.
The Fe 3+/∑Fe ratio of bridgmanite dictates the whole‐rock Fe 3+/∑Fe ratio and, for pyrolite and harzburgite, appears to affect velocity gradients dv / dz with higher Fe 3+/∑Fe ratios leading to steeper gradients dv / dz . Again, the effect seems to be strongest for S waves. Based on a comparison of computed P‐ and S‐ wave velocity gradients of pyrolite with PREM, Kurnosov et al. (2017) argued for a reduction of the ferric iron content in bridgmanite with depth. While a steepening of velocity gradients with higher Fe 3+/∑Fe ratios of bridgmanite is consistent with the modeling results presented here, an actual match of a pyrolitic bulk composition with PREM seems only possible for S‐ wave velocities and at depths in excess of 1500 km. Assuming a Fe‐Mg exchange coefficient of 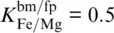 , modeled S‐ wave velocities match those of PREM at about 1600 km depth for Fe 3+/∑Fe = 1 in bridgmanite. To maintain d ln v S= 0 at depths greater than 1600 km, the Fe 3+/∑Fe ratio of bridgmanite would then need to gradually decrease with increasing depth. For harzburgite, the impact of the Fe 3+/∑Fe ratio of bridgmanite on P‐ and S‐ wave velocity profiles is complicated by the stabilization of a Fe 2O 3component for high Fe 3+/Al ratios in bridgmanite due to the lower overall Al 2O 3content of harzburgite. As long as sufficient aluminum is available, ferric iron is preferentially incorporated into bridgmanite as the component FeAlO 3(Frost & Langenhorst, 2002; Richmond & Brodholt, 1998; Zhang & Oganov, 2006). While iron cations of the FeSiO 3and FeAlO 3components of bridgmanite replace magnesium on the dodecahedral A site and remain in high‐spin states at pressures of the lower mantle (Catalli et al., 2010; Jackson et al., 2005a; Lin et al., 2016), one Fe 3+cation of the Fe 2O 3component is located on the octahedral B site and goes through a spin transition at pressures above 40 GPa (Catalli et al., 2010; Liu et al., 2018). For the modeling results shown in Figure 3.9, Fe 3+/Al ratios in bridgmanite become high enough to stabilize the Fe 2O 3component only for harzburgite models with Fe 3+/∑Fe > 0.5 or
, modeled S‐ wave velocities match those of PREM at about 1600 km depth for Fe 3+/∑Fe = 1 in bridgmanite. To maintain d ln v S= 0 at depths greater than 1600 km, the Fe 3+/∑Fe ratio of bridgmanite would then need to gradually decrease with increasing depth. For harzburgite, the impact of the Fe 3+/∑Fe ratio of bridgmanite on P‐ and S‐ wave velocity profiles is complicated by the stabilization of a Fe 2O 3component for high Fe 3+/Al ratios in bridgmanite due to the lower overall Al 2O 3content of harzburgite. As long as sufficient aluminum is available, ferric iron is preferentially incorporated into bridgmanite as the component FeAlO 3(Frost & Langenhorst, 2002; Richmond & Brodholt, 1998; Zhang & Oganov, 2006). While iron cations of the FeSiO 3and FeAlO 3components of bridgmanite replace magnesium on the dodecahedral A site and remain in high‐spin states at pressures of the lower mantle (Catalli et al., 2010; Jackson et al., 2005a; Lin et al., 2016), one Fe 3+cation of the Fe 2O 3component is located on the octahedral B site and goes through a spin transition at pressures above 40 GPa (Catalli et al., 2010; Liu et al., 2018). For the modeling results shown in Figure 3.9, Fe 3+/Al ratios in bridgmanite become high enough to stabilize the Fe 2O 3component only for harzburgite models with Fe 3+/∑Fe > 0.5 or 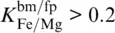 . The elastic softening of the bulk modulus due to the spin transition of Fe 3+on the B site of bridgmanite (Fu et al., 2018) significantly reduces P‐ wave velocities for the respective harzburgite models at pressures between 40 and 100 GPa. The low overall Al 2O 3content affects both P‐ and S‐ wave velocities.
. The elastic softening of the bulk modulus due to the spin transition of Fe 3+on the B site of bridgmanite (Fu et al., 2018) significantly reduces P‐ wave velocities for the respective harzburgite models at pressures between 40 and 100 GPa. The low overall Al 2O 3content affects both P‐ and S‐ wave velocities.
While dominated by the elastic softening due to the ferroelastic phase transition between stishovite and CaCl 2‐type SiO 2, modeled P‐ and S‐ wave velocity profiles of metabasalt are sensitive to both the Fe 3+/∑Fe ratio of bridgmanite and Fe‐Mg exchange between bridgmanite and the CF phase. In contrast to pyrolite and harzburgite, higher Fe 3+/∑Fe ratios appear to reduce velocity gradients with depths. Varying the Fe‐Mg exchange coefficient between bridgmanite and the CF phase has the opposing effect and results in higher P‐ and S‐ wave velocities for higher values of the Fe‐Mg exchange coefficient. For all three bulk rock compositions addressed here, the sensitivity of P‐ and S‐ wave velocities to variations in Fe‐Mg exchange coefficients demonstrates the need for better constraining equilibrium mineral compositions at relevant pressures and temperatures. While Fe‐Mg exchange coefficients and Fe 3+/∑Fe ratios were treated here as independent parameters, they are coupled through the preferred incorporation of ferric iron into bridgmanite (Frost et al., 2004; Irifune et al., 2010). As shown in Figure 3.6, however, available data on element partitioning cannot unambiguously constrain mineral compositions. More experiments and thermodynamic data are required to improve forward models of the petrology and elastic properties of lower‐mantle rocks.
To depict the effect of continuous phase transitions on modeled P‐ and S‐ wave velocities, I computed additional velocity profiles by ignoring changes in spin states of iron cations and by suppressing the phase transition from stishovite to CaCl 2‐type SiO 2. The results are included in Figure 3.9for each reference scenario and for selected combinations of compositional parameters that are expected to be particularly susceptible to the effects of spin transitions. All pyrolite models as well as the reference scenario for harzburgite are only affected by the spin transition of ferrous iron in ferropericlase as no ferric iron is expected to enter the B site of bridgmanite for the respective combinations of Fe‐Mg exchange coefficients and Fe 3+/∑Fe ratios of bridgmanite. Along an adiabatic compression path, the spin transition of Fe 2+in ferropericlase broadens substantially for reasons discussed in Section 3.7and mainly reduces P‐ wave velocities. As mentioned earlier, Fe 3+is found to enter the crystallographic B site of bridgmanite only for harzburgite models with Fe 3+/∑Fe > 0.5 or  . For these scenarios, the spin transition of Fe 3+on the B site of bridgmanite gives rise to an additional P‐ wave velocity reduction over a pressure interval from 40 to 100 GPa. Despite substantial broadening of the Fe 2+spin transition in ferropericlase and the Fe 3+spin transition in bridgmanite at high temperatures, both spin transitions can significantly reduce P‐ wave velocities of pyrolite and harzburgite and need to be taken into account when modeling elastic properties. In addition, the spin transition in ferropericlase is further expected to affect Fe‐Mg exchange between ferropericlase and bridgmanite (Badro, 2014; Badro et al., 2005, 2003; Lin et al., 2013). Given the strong sensitivity of both P‐ and S‐ wave velocities to changes in the Fe‐Mg exchange coefficient, the spin transition in ferropericlase could have a compositional effect on seismic properties that surpasses the elastic effect. Increasing the iron content of ferropericlase will also shift the spin transition to higher pressures (Fei et al., 2007; Persson et al., 2006; Solomatova et al., 2016; Speziale et al., 2005). Since S‐ wave velocities are more sensitive to Fe‐Mg exchange than P‐ wave velocities, the compositional contribution would strongly affect S‐ wave velocities as opposed to the elastic contribution that mostly affects P‐ wave velocities via elastic softening of the bulk modulus.
. For these scenarios, the spin transition of Fe 3+on the B site of bridgmanite gives rise to an additional P‐ wave velocity reduction over a pressure interval from 40 to 100 GPa. Despite substantial broadening of the Fe 2+spin transition in ferropericlase and the Fe 3+spin transition in bridgmanite at high temperatures, both spin transitions can significantly reduce P‐ wave velocities of pyrolite and harzburgite and need to be taken into account when modeling elastic properties. In addition, the spin transition in ferropericlase is further expected to affect Fe‐Mg exchange between ferropericlase and bridgmanite (Badro, 2014; Badro et al., 2005, 2003; Lin et al., 2013). Given the strong sensitivity of both P‐ and S‐ wave velocities to changes in the Fe‐Mg exchange coefficient, the spin transition in ferropericlase could have a compositional effect on seismic properties that surpasses the elastic effect. Increasing the iron content of ferropericlase will also shift the spin transition to higher pressures (Fei et al., 2007; Persson et al., 2006; Solomatova et al., 2016; Speziale et al., 2005). Since S‐ wave velocities are more sensitive to Fe‐Mg exchange than P‐ wave velocities, the compositional contribution would strongly affect S‐ wave velocities as opposed to the elastic contribution that mostly affects P‐ wave velocities via elastic softening of the bulk modulus.
Читать дальше


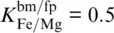 , modeled S‐ wave velocities match those of PREM at about 1600 km depth for Fe 3+/∑Fe = 1 in bridgmanite. To maintain d ln v S= 0 at depths greater than 1600 km, the Fe 3+/∑Fe ratio of bridgmanite would then need to gradually decrease with increasing depth. For harzburgite, the impact of the Fe 3+/∑Fe ratio of bridgmanite on P‐ and S‐ wave velocity profiles is complicated by the stabilization of a Fe 2O 3component for high Fe 3+/Al ratios in bridgmanite due to the lower overall Al 2O 3content of harzburgite. As long as sufficient aluminum is available, ferric iron is preferentially incorporated into bridgmanite as the component FeAlO 3(Frost & Langenhorst, 2002; Richmond & Brodholt, 1998; Zhang & Oganov, 2006). While iron cations of the FeSiO 3and FeAlO 3components of bridgmanite replace magnesium on the dodecahedral A site and remain in high‐spin states at pressures of the lower mantle (Catalli et al., 2010; Jackson et al., 2005a; Lin et al., 2016), one Fe 3+cation of the Fe 2O 3component is located on the octahedral B site and goes through a spin transition at pressures above 40 GPa (Catalli et al., 2010; Liu et al., 2018). For the modeling results shown in Figure 3.9, Fe 3+/Al ratios in bridgmanite become high enough to stabilize the Fe 2O 3component only for harzburgite models with Fe 3+/∑Fe > 0.5 or
, modeled S‐ wave velocities match those of PREM at about 1600 km depth for Fe 3+/∑Fe = 1 in bridgmanite. To maintain d ln v S= 0 at depths greater than 1600 km, the Fe 3+/∑Fe ratio of bridgmanite would then need to gradually decrease with increasing depth. For harzburgite, the impact of the Fe 3+/∑Fe ratio of bridgmanite on P‐ and S‐ wave velocity profiles is complicated by the stabilization of a Fe 2O 3component for high Fe 3+/Al ratios in bridgmanite due to the lower overall Al 2O 3content of harzburgite. As long as sufficient aluminum is available, ferric iron is preferentially incorporated into bridgmanite as the component FeAlO 3(Frost & Langenhorst, 2002; Richmond & Brodholt, 1998; Zhang & Oganov, 2006). While iron cations of the FeSiO 3and FeAlO 3components of bridgmanite replace magnesium on the dodecahedral A site and remain in high‐spin states at pressures of the lower mantle (Catalli et al., 2010; Jackson et al., 2005a; Lin et al., 2016), one Fe 3+cation of the Fe 2O 3component is located on the octahedral B site and goes through a spin transition at pressures above 40 GPa (Catalli et al., 2010; Liu et al., 2018). For the modeling results shown in Figure 3.9, Fe 3+/Al ratios in bridgmanite become high enough to stabilize the Fe 2O 3component only for harzburgite models with Fe 3+/∑Fe > 0.5 or 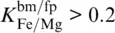 . The elastic softening of the bulk modulus due to the spin transition of Fe 3+on the B site of bridgmanite (Fu et al., 2018) significantly reduces P‐ wave velocities for the respective harzburgite models at pressures between 40 and 100 GPa. The low overall Al 2O 3content affects both P‐ and S‐ wave velocities.
. The elastic softening of the bulk modulus due to the spin transition of Fe 3+on the B site of bridgmanite (Fu et al., 2018) significantly reduces P‐ wave velocities for the respective harzburgite models at pressures between 40 and 100 GPa. The low overall Al 2O 3content affects both P‐ and S‐ wave velocities. . For these scenarios, the spin transition of Fe 3+on the B site of bridgmanite gives rise to an additional P‐ wave velocity reduction over a pressure interval from 40 to 100 GPa. Despite substantial broadening of the Fe 2+spin transition in ferropericlase and the Fe 3+spin transition in bridgmanite at high temperatures, both spin transitions can significantly reduce P‐ wave velocities of pyrolite and harzburgite and need to be taken into account when modeling elastic properties. In addition, the spin transition in ferropericlase is further expected to affect Fe‐Mg exchange between ferropericlase and bridgmanite (Badro, 2014; Badro et al., 2005, 2003; Lin et al., 2013). Given the strong sensitivity of both P‐ and S‐ wave velocities to changes in the Fe‐Mg exchange coefficient, the spin transition in ferropericlase could have a compositional effect on seismic properties that surpasses the elastic effect. Increasing the iron content of ferropericlase will also shift the spin transition to higher pressures (Fei et al., 2007; Persson et al., 2006; Solomatova et al., 2016; Speziale et al., 2005). Since S‐ wave velocities are more sensitive to Fe‐Mg exchange than P‐ wave velocities, the compositional contribution would strongly affect S‐ wave velocities as opposed to the elastic contribution that mostly affects P‐ wave velocities via elastic softening of the bulk modulus.
. For these scenarios, the spin transition of Fe 3+on the B site of bridgmanite gives rise to an additional P‐ wave velocity reduction over a pressure interval from 40 to 100 GPa. Despite substantial broadening of the Fe 2+spin transition in ferropericlase and the Fe 3+spin transition in bridgmanite at high temperatures, both spin transitions can significantly reduce P‐ wave velocities of pyrolite and harzburgite and need to be taken into account when modeling elastic properties. In addition, the spin transition in ferropericlase is further expected to affect Fe‐Mg exchange between ferropericlase and bridgmanite (Badro, 2014; Badro et al., 2005, 2003; Lin et al., 2013). Given the strong sensitivity of both P‐ and S‐ wave velocities to changes in the Fe‐Mg exchange coefficient, the spin transition in ferropericlase could have a compositional effect on seismic properties that surpasses the elastic effect. Increasing the iron content of ferropericlase will also shift the spin transition to higher pressures (Fei et al., 2007; Persson et al., 2006; Solomatova et al., 2016; Speziale et al., 2005). Since S‐ wave velocities are more sensitive to Fe‐Mg exchange than P‐ wave velocities, the compositional contribution would strongly affect S‐ wave velocities as opposed to the elastic contribution that mostly affects P‐ wave velocities via elastic softening of the bulk modulus.










