Mantle Convection and Surface Expressions

Lowell Miyagi

Geology and Geophysics, University of Utah, Salt Lake City, UT, USA

Plastic deformation of rocks and mineral phases in the Earth’s interior plays a primary role in controlling large‐scale dynamic processes such as mantle convection and associated plate tectonics. Volumetrically, the lower mantle is the largest region of the Earth, and thus great effort has been made to study the deformation behavior of the mineral phases that comprise the lower mantle. Plastic deformation of these rocks and mineral phases can also lead to preferred orientation development (texture), which, in turn, can result in anisotropic physical properties. Many regions of the Earth’s interior exhibit seismic anisotropy, and thus, considerable effort has been made to understand the processes leading to texture and anisotropy development in deep Earth phases. Studying deformation of lower mantle materials is technically challenging due to the extreme pressures and temperatures experienced by materials in the deep Earth. However, recent technological advances have allowed significant progress to be made toward understanding the deformation behavior of lower mantle phases. This chapter provides an overview of deformation mechanisms in lower mantle materials and the current state of experimental deformation studies on lower mantle mineral phases and polyphase aggregates of materials relevant to the lower mantle.

Large‐scale geodynamic phenomena such as post‐glacial rebound, mantle convection, slab subduction, and plate motion are intimately linked to plastic deformation of minerals and rocks in the Earth’s deep interior. The lower mantle, which ranges from the 660 km seismic discontinuity and continues to the core mantle boundary (CMB) at ~2900 km depth, constitutes ~55% of the Earth by volume, and thus lower mantle properties play a fundamental role in controlling much of Earth’s dynamic behavior. As such, considerable effort has been directed at parameterizing rheological behavior of mantle rocks and minerals at high pressure and temperature conditions. For studying geodynamic behavior, the goal is generally to understand the stress–strain rate response of rocks and minerals in order to characterize viscosity of mantle materials. This behavior can change dramatically with changes in pressure, temperature, composition, and grain size (Cordier & Goryaeva, 2018; Frost & Ashby, 1982; Karato, 2010; Marquardt & Miyagi, 2015). Thus, a major area of research is to determine and quantify variations in stress–strain rate response of these materials as a function of these conditions. In addition to flow laws, great interest has been generated in understanding the relationship between deformation and anisotropy in mantle rocks. Seismic anisotropy is observed in many regions of the Earth’s interior and is widely believed to be due to deformation‐induced texture (crystallographic preferred orientation) of constituent mineral phases in the Earth’s interior (Karato, 1998; Karato et al., 2007; Long & Becker, 2010; Romanowicz & Wenk, 2017). If one has a detailed understanding of the mechanisms of texture development and the relationship between deformation, texture, and anisotropy, then one can use observations of seismic anisotropy to infer mantle flow patterns in the deep Earth (Chandler et al., 2018; Cottaar et al., 2014; Long & Becker, 2010; Nowacki et al., 2010, 2011; Tommasi et al., 2018; Walker et al., 2011, 2018).

Although the exact mineralogy and chemistry of the lower mantle is still debated, seismic velocities and densities of the lower mantle are consistent with a mineralogy composed predominantly (65% to 85% by volume) of (Mg,Fe)(Si,Al,Fe)O 3bridgmanite (Brg) with (Mg,Fe)O ferropericlase (Fp) as the second‐most abundant phase, and a few percent of CaSiO 3perovskite (Ca‐Pv) (e.g., Kurnosov et al., 2017; Matas et al., 2007; Mattern et al., 2005). At conditions similar to those of the D” (~2700 km), Brg undergoes a solid‐solid phase transformation to a post‐perovskite structured phase (pPv) (Murakami et al., 2004; Oganov & Ono, 2004; Shim et al., 2004). The stability and depth of this phase transition varies considerably depending on chemical composition (Grocholski et al., 2012), but pPv is likely to be a major phase at least in localized regions above the CMB. Iron content in the lower mantle is likely to be in the 10 mole % range (Matas et al., 2007) but the partitioning of iron between Fp, Brg, and pPv is not fully constrained (e.g., Piet et al., 2016). This chapter will focus on reviewing the current state of deformation experiments on the major lower mantle phases (Brg, Ca‐Pv, pPv, and Fp) with a discussion of the current knowledge of deformation mechanisms in these phases and the potential for interactions between phases when deformed in a polyphase rock.

In high‐pressure laboratory experiments, minerals deform by several mechanisms. At high temperatures and low stress, crystals deform by motion of point defects through grains and/or along grain boundaries. These types of diffusion creep are typically referred to as Nabbaro‐Herring Creep (Herring, 1950; Nabarro, 1948) and Coble Creep (Coble, 1963), respectively. While there are some subtle rheological differences between flow dominated by each of these mechanisms, generally speaking, diffusion creep leads to a Newtonian rheology – that is, a linear stress–strain rate relationship. Strain rate ( in the diffusion creep regime is generally written in the following form:

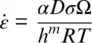
where α is a parameter that describes the contribution of grain boundary sliding, D is the diffusion coefficient, σ is stress, Ω is atomic volume, h is grain size, m is 2–3, R is the gas constant (8.314510 J/mol∙K), and T is temperature. Grain size dependence comes about because efficiency of diffusion is strongly dependent on length scale ( D ≈ l 2/ t ) and thus diffusion creep is efficient only over short lengths, i.e., small grain sizes. Diffusion coefficients have an Arrhenius type relationship with temperature (Arrhenius, 1889; van’t Hoff, 1884). The effect of pressure can also be included, leading to a temperature and pressure dependence of the diffusion coefficient, which is given by

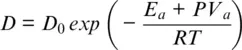
where D 0is termed the frequency factor, E ais activation energy and V ais the activation volume (e.g., Poirier, 1985). Thus, high temperature increases the efficiency of diffusion creep while pressure lowers efficacy. Thus, viscosity of a mineral will generally decrease with temperature and increase with pressure.

On the other end of the spectrum, at high stress and low temperatures, plasticity occurs by dislocation glide. Dislocations accommodate strain through the propagation of linear defects through a crystal. Dislocations occur on a slip system that is characterized by a plane (hkl) and a direction . Shearing along the slip plane in the slip direction results in an offset in the crystal lattice thus accommodating shear strain. Resistance to glide is controlled by the Peierls stress (Nabarro, 1947; Peierls, 1940). For a monoatomic lattice, the Peierls stress ( σ p) is given by