Gene Cheung - Graph Spectral Image Processing

[1.49]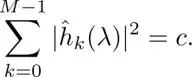

If c = 1, the frame is called a Parseval frame . In this case, it conserves the energy of the original signal in the transformed domain. Tight spectral graph filter banks can be constructed by employing the design methods of tight frames in classical signal processing. Examples can be found in Leonardi and Van De Ville (2013); Shuman et al. (2015); Sakiyama et al. (2016).

Constructing perfect reconstruction graph transforms with sampling is much more difficult than the undecimated version. However, it is required as the storage cost can be increased tremendously for the undecimated versions, especially for signals on a very large graph. Though the general condition is given by equation [1.42], the challenges are designing and choosing the appropriate sampling operator S kand the appropriate filters h k( L) and g k( L). The perfect reconstruction condition can be satisfied with proper sets of these.

Various methodologies have been proposed in literature with different strategies. The recent methods of such transforms are summarized in Sakiyama et al. (2019c). We have omitted these details because they are beyond the scope of this chapter. Instead, some design guidelines are listed as follows:

– Sampling operator: In GSP, two different definitions of sampling operators exist (Tanaka et al. 2020; Tanaka 2018; Tanaka and Eldar 2020). One is vertex domain sampling, which is an analog of time-domain sampling. The other is graph frequency domain sampling, which is a counterpart of the Fourier domain expression of sampling. Both are not interchangeable in general, and have their own advantages and disadvantages.

– Localized transform: As mentioned later in section 1.6.5, polynomial filters are localized in the vertex domain. Furthermore, if all filters are polynomials, the entire transform can be eigendecomposition free, and thus, its computation decreases significantly.

– Flexible design adapting various spectra: Different graphs have unique eigenvalue distributions, and different graph operators have unique characteristics. Additionally, we sometimes encounter repeated eigenvalues. A unified design strategy is required for representing various graph signals sparsely.

As we mentioned in the previous sections, a naïve implementation of spectral graph filters often requires a high computational complexity. Since we often need to process high-resolution images, reducing such a complexity would be a high priority. Moreover, spectral filtering is often iteratively employed for image restoration, like an internal algorithm for convex optimization problems. In this section, we describe a workaround to alleviate computational burden for graph spectral filtering.

Digital image processing has a long history, and the subdivision of images has been widely used for various image processing tasks. For example, JPEG and MPEG image/video compression standards still use block-based predictions and transforms, even in their most recent standards. Moreover, graph-based image processing also uses such a subdivision as preprocessing. It can also be combined with the following fast computation approaches.

A simple solution for image subdivision is the block-based approach. It divides the input image into an equal-sized subblocks (these blocks can be overlapped with an appropriate window function), after which the favorite image processing tasks can be performed. The advantage it provides is simplicity: we only have to consider the size of subblocks to make a trade-off between performance and complexity. Sizes of the consistent image regions vary significantly; as a result, a recursive subdivision, called quadtree decomposition, provides a good trade-off.

More complex image subdivisions are also possible by utilizing an image segmentation. Although these segmentated sub-images are not rectangular in general, we can directly perform graph-based image processing in such non-rectangular regions by using appropriate graphs.

Downsampling is another typical approach for reducing the computation cost, and this has been used everywhere in image processing applications. A challenge for graph-based image processing is to find a good low-resolution graph, which properly reflects the original pixel structure.

Reducing the size of a graph is called graph reduction or graph coarsening . It is divided into two phases:

1) Phase 1: reducing the number of nodes;

2) Phase 2: reconnecting edges for the downsampled pixels.

In image processing, Phase 1 is relatively straightforward. We can assume the original image pixels are nodes on a uniform grid. As in usual image processing, picking up every other node (when the image signal is downsampled by two) will be reasonable.

For more general graphs like those used in point cloud processing, we need to select the “best” set of nodes. This problem is called sampling set selection . Although this is beyond our scope in this chapter, please refer to (Tanaka et al . 2020; Sakiyama et al . 2019c) and references therein.

In contrast to Phase 1, Phase 2 is not very straightforward. If pixels in the original image/block are associated with a graph, the downsampled one should be reconnected by edges, such that the reduced-size graph reflects the original structure. In the general

GSP study, desiderata for the reduced-size graphs have been suggested in Shuman et al. (2016a) as follows:

1) the reduced-size graph has non-negative edge weights;

2) the connectivity of the original graph is preserved in the reduced-size graphs;

3) the spectrum of the reduced-size graph is representative of the original graph;

4) the reduced-size graph preserves the original structural properties;

5) if two nodes are connected in the original graph, they should have a similar edge weights in the reduced-size graph;

6) it is tractable in terms of implementation and computational complexity;

7) the reduced-size graph preserves the sparsity (i.e. the ratio between the number of nonzero edges and that of pixels) of the original one.

Existing reconnection methods do not always satisfy all of these simultaneously; however, they do exhibit some of these properties. The order of the desired properties depends on applications considered. Major approaches have been summarized in Shuman et al. (2016a).

If an image or subblock has several typical patterns, i.e. graphs, precomputing GFT bases for these graphs may be a reasonable choice to decrease the computational burden. This is because when we use them off the shelf, the computation cost reduces significantly as a result of decreased complexity, with a sacrifice of the storage cost for the GFT matrices and the cost of searching the optimal precomputed GFT from a given image. This precomputing strategy is popular in standard image processing. For example, in modern image/video coding standards, some precomputed transforms, such as DCT and discrete sine transform (DST) with various sizes, are utilized to represent image blocks as sparsely as possible.