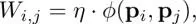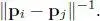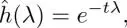1 ...7 8 9 11 12 13 ...17 For the classical Fourier domain filtering, it is enough to consider the frequency range ω ∈ [ − π, π ] (or an arbitrary 2 π interval). However, graph frequency varies according to an underlying graph and/or the chosen graph operator. For example, symmetric normalized graph Laplacians have eigenvalues within [0, 2], whereas combinatorial graph Laplacians do not have such a graph-independent maximum bound. The simple maximum bound of combinatorial graph Laplacian is, for example, given as (Anderson Jr and Morley 1985)
[1.16] 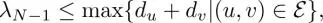
where d uis the degree of the vertex u . Several other improvements on the bound are also found in literature. Although the graph Laplacians mentioned above have a bound of the largest eigenvalue, such bounds are not applicable to the adjacency matrix. Considering this, appropriate care of the graph frequency range must be taken while designing graph filters.
As mentioned, graph frequency domain filtering is an analog of Fourier domain filtering. However, this does not mean we always obtain a vertex domain expression of this similar to equation [1.9]. Hence, we need to compute the GFT of the input signal, which raises a computational issue described as follows. For the GFT, the eigenvector matrix Uhas to be calculated from the graph operator. The eigendecomposition requires 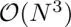 complexity for a dense matrix 2 . This calculation often becomes increasingly complex, especially for big data applications, including image processing.
complexity for a dense matrix 2 . This calculation often becomes increasingly complex, especially for big data applications, including image processing.
Typically, graph spectral image processing vectorizes image pixels. Let us assume that we have a grayscale image of size W × H pixels. Its vectorized version is 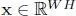 and its corresponding graph operator would be
and its corresponding graph operator would be 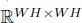 . For example, 4K ultra-high-definition resolution corresponds to W = 3, 840 and H = 2, 160, which leads to WH > 8 × 10 6: this is too large to perform eigendecomposition, even for a recent high-spec computer. In section 1.6, several fast computation methods of graph spectral filtering will be discussed to alleviate this problem.
. For example, 4K ultra-high-definition resolution corresponds to W = 3, 840 and H = 2, 160, which leads to WH > 8 × 10 6: this is too large to perform eigendecomposition, even for a recent high-spec computer. In section 1.6, several fast computation methods of graph spectral filtering will be discussed to alleviate this problem.
1.3.3. Relationship between graph spectral filtering and classical filtering
Filtering in the graph frequency domain seems to be an intuitive extension of Fourier domain filtering into the graph setting. In fact, it coincides with time-domain filtering in a special case, beyond the intuition.
Suppose that the underlying graph is a cycle graph with length N , and its graph Laplacian L cycleis assumed as follows:
[1.17] 
where its blank elements are zero. It is well known that the eigenvector matrix of L cycleis the DFT (Strang 1999), i.e.
[1.18] 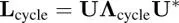
in which
[1.19] 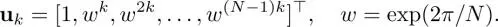
In other words, when we consider a cycle graph and assume its associated graph Laplacian is L cycle, its GFT is the DFT. Therefore, graph spectral filtering in equation [1.13]is identical to the time-domain filtering. Note that, while Uis the DFT, the interval of its eigenvalues is not equal to 2 πk/N . Specificallly, the k th eigenvalue of L cycleis λ k= 2 − 2cos(2 πk/N ).
1.4. Edge-preserving smoothing of images as graph spectral filters
This book (especially this chapter) focuses on graph spectral domain operations for image processing. Here, we describe interconnections between well-studied edge preserving filters and their GSP-based representations. As previously mentioned in this section, pixel-dependent filters do not have frequency domain expressions in a classical sense. This is because the impulse responses vary for different pixel index values n . In the following, we show that such a pixel-dependent filter can be viewed as a graph spectral filter, i.e. it presents a diagonal graph frequency response. Roughly speaking, GSP-based image processing considers the pixel structure and the filter kernel independently. Therefore, the pixel-dependent processing can be performed with a fixed filter kernel, owing to the underlying graph.
Let us begin with the history before the GSP era. In the mid-1990s, Taubin proposed seminal works on smoothing using graph spectral analysis for 3D mesh processing (Taubin 1995; Taubin et al. 1996) 3 . He determined the edge weights of polygon meshes using the Euclidean (geometric) distance between nodes. Assuming 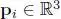 as a 3-D coordinate of the i th node, the edge weight is then defined as
as a 3-D coordinate of the i th node, the edge weight is then defined as
[1.20] 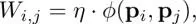
where η is the normalizing factor and φ ( p i , p j) is a non-negative function, which assigns a large weight if p iand p jare close. The typical choice of φ ( p i , p j) will be 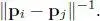
The matrix Wis symmetric. If we choose φ ( p i , p i) = 0, its diagonal elements would become zero, and as a result, Wcould be viewed as a normalized adjacency matrix. The coordinates are then smoothed by a graph low-pass filter, after computing the GFT basis U. Similar approaches to this method have been used in several computer graphics/vision tasks (Zhang et al. 2010; Vallet and Lévy 2008; Desbrun et al. 1999; Fleishman et al. 2003; Kim and Rossignac 2005).
For image smoothing, filtering with a heat kernel represented in the graph frequency domain has also been proposed by Zhang and Hancock (2008). In this work, the edge weights of the pixel graph are computed according to photometric distance, i.e. large weights are assigned to the edges whose ends have similar pixel values and vice versa. Additionally, the graph spectral filter is defined as a solution for the heat equation on the graph, and is expressed as follows:
[1.21] 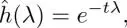
Читать дальше

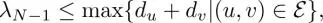
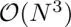 complexity for a dense matrix 2 . This calculation often becomes increasingly complex, especially for big data applications, including image processing.
complexity for a dense matrix 2 . This calculation often becomes increasingly complex, especially for big data applications, including image processing.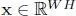 and its corresponding graph operator would be
and its corresponding graph operator would be 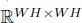 . For example, 4K ultra-high-definition resolution corresponds to W = 3, 840 and H = 2, 160, which leads to WH > 8 × 10 6: this is too large to perform eigendecomposition, even for a recent high-spec computer. In section 1.6, several fast computation methods of graph spectral filtering will be discussed to alleviate this problem.
. For example, 4K ultra-high-definition resolution corresponds to W = 3, 840 and H = 2, 160, which leads to WH > 8 × 10 6: this is too large to perform eigendecomposition, even for a recent high-spec computer. In section 1.6, several fast computation methods of graph spectral filtering will be discussed to alleviate this problem.
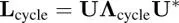
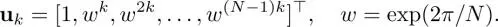
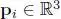 as a 3-D coordinate of the i th node, the edge weight is then defined as
as a 3-D coordinate of the i th node, the edge weight is then defined as