Generalized Ordinary Differential Equations in Abstract Spaces and Applications

Thus,

and the proof is complete.

With Theorem 1.49at hand, the next corollary follows immediately.

Corollary 1.50: The following statements hold:

1 If and , then .

2 If and , then .

Next, we state a uniform convergence theorem for Perron–Stieltjes vector integrals. A proof of such result can be found in [210, Theorem 11].

Theorem 1.51: Let and , , be such that the Perron–Stieltjes integral exists for every and uniformly in . Then, exists and

We finish this subsection by presenting a Grönwall‐type inequality for Perron–Stieltjes integrals. For a proof of it, we refer to [209, Corollary 1.43].

Theorem 1.52 (Grönwall Inequality): Let be a nondecreasing left‐continuous function, and . Assume that is bounded and satisfies

Then,

Other properties of Perron–Stieltjes integrals can be found in Chapter 2, where they appear within the consequences of the main results presented there.

The first result of this section is an Integration by Parts Formula for Riemann–Stieltjes integrals. It is a particular consequence of Proposition 1.70presented in the end of this section. A proof of it can be found in [126, Theorem II.1.1].

Theorem 1.53 (Integration by Parts): Let be a BT. Suppose

1 either and ;

2 or and .

Then, and , that is, the Riemann–Stieltjes integrals and exist, and moreover,

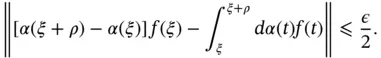
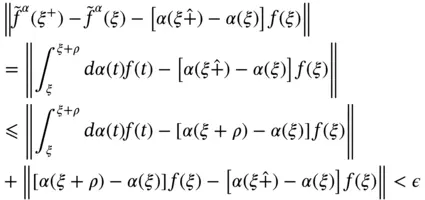
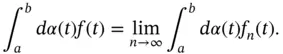
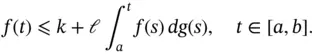
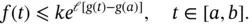
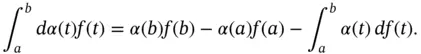
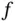Next, we state a result which is not difficult to prove using the definitions involved in the statement. See [72, Theorem 5]. Recall that the indefinite integral of a function in is denoted by (see Definition 1.42)

Theorem 1.54: Suppose and is bounded. Then and

(1.3)

If, in addition, , then .

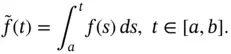
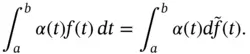
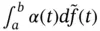By Theorem 1.47, the Perron–Stieltjes integral exists and the next corollary follows.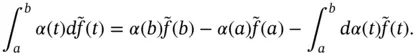

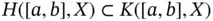Corollary 1.55: Let and be such that . Then, and (1.3) holds.

A second corollary of Theorem 1.54follows by the fact that Riemann–Stieltjes integrals are special cases of Perron–Stieltjes integrals. Then, it suffices to apply Theorems 1.49and 1.53.

Corollary 1.56: Suppose the following conditions hold:

1 either and , with ;

2 or and .

Then, , equality (1.3) holds, and we have

(1.4)

The next theorem is due to C. S. Hönig (see [129]), and it concerns multipliers for Perron–Stieltjes integrals.

Theorem 1.57: Suppose and . Then, and Eqs. (1.3) and (1.4) hold.

Since and 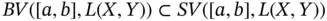, it is immediate that if 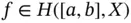and 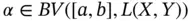, then 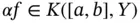. As a matter of fact, the next result gives us information about the multipliers for the Henstock vector integral. See [72, Theorem 7].

Theorem 1.58: Assume that and . Then, and equalities (1.3) and (1.4) hold.

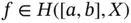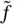Proof. Since , is continuous by Theorem 1.49. Thus, given 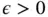, there exists 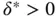such that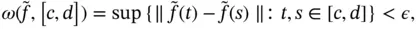

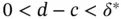whenever , where . Moreover, there is a gauge 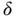on 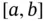, with 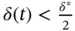for 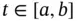, such that for every 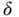‐fine 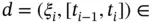,
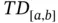