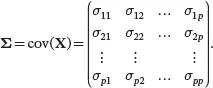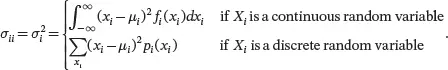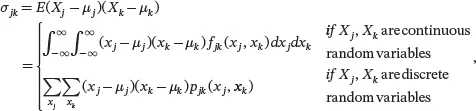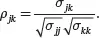Yong Chen - Industrial Data Analytics for Diagnosis and Prognosis
Здесь есть возможность читать онлайн «Yong Chen - Industrial Data Analytics for Diagnosis and Prognosis» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Industrial Data Analytics for Diagnosis and Prognosis
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Industrial Data Analytics for Diagnosis and Prognosis: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Industrial Data Analytics for Diagnosis and Prognosis»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
In
, distinguished engineers Shiyu Zhou and Yong Chen deliver a rigorous and practical introduction to the random effects modeling approach for industrial system diagnosis and prognosis. In the book’s two parts, general statistical concepts and useful theory are described and explained, as are industrial diagnosis and prognosis methods. The accomplished authors describe and model fixed effects, random effects, and variation in univariate and multivariate datasets and cover the application of the random effects approach to diagnosis of variation sources in industrial processes. They offer a detailed performance comparison of different diagnosis methods before moving on to the application of the random effects approach to failure prognosis in industrial processes and systems.
In addition to presenting the joint prognosis model, which integrates the survival regression model with the mixed effects regression model, the book also offers readers:
A thorough introduction to describing variation of industrial data, including univariate and multivariate random variables and probability distributions Rigorous treatments of the diagnosis of variation sources using PCA pattern matching and the random effects model An exploration of extended mixed effects model, including mixture prior and Kalman filtering approach, for real time prognosis A detailed presentation of Gaussian process model as a flexible approach for the prediction of temporal degradation signals Ideal for senior year undergraduate students and postgraduate students in industrial, manufacturing, mechanical, and electrical engineering,
is also an indispensable guide for researchers and engineers interested in data analytics methods for system diagnosis and prognosis.

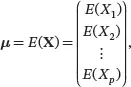
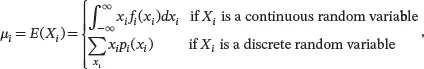
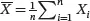 is a random variable because the observations X 1, X 2,…, Xn are all random variables with values varying from sample to sample. For example, let X represent the measured intensity of the current of a wafer produced by a semiconductor manufacturing process. Then we take a random sample of n = 10 wafers from this process and compute the sample mean of the measured intensities of the current and get the result x̄ = 1.02. Now we repeat this process, taking a second sample of n = 10 wafers from the same process and the resulting sample mean is 1.04. The sample means differ from sample to sample because they are random variables. Consequently, the sample mean, and any other function of the random observations, is a random variable. On the other hand, the population mean µ does not depend on the samples and is a (usually unknown) constant. When we take a sample with very large sample size n , the sample mean will be very close to the population mean µ with high probability. As the sample mean X̄ is a random variable, we can evaluate its mean and variance. It is easy to see that E ( X̄ ) = µ and var ( X̄ ) = σ 2/ n , where β 2is the variance of X . An estimator of a parameter is called unbiased if its mean is equal to the true value of the parameter. X̄ is a commonly used estimator of µ because it is unbiased and has a smaller variance for a larger sample size n .
is a random variable because the observations X 1, X 2,…, Xn are all random variables with values varying from sample to sample. For example, let X represent the measured intensity of the current of a wafer produced by a semiconductor manufacturing process. Then we take a random sample of n = 10 wafers from this process and compute the sample mean of the measured intensities of the current and get the result x̄ = 1.02. Now we repeat this process, taking a second sample of n = 10 wafers from the same process and the resulting sample mean is 1.04. The sample means differ from sample to sample because they are random variables. Consequently, the sample mean, and any other function of the random observations, is a random variable. On the other hand, the population mean µ does not depend on the samples and is a (usually unknown) constant. When we take a sample with very large sample size n , the sample mean will be very close to the population mean µ with high probability. As the sample mean X̄ is a random variable, we can evaluate its mean and variance. It is easy to see that E ( X̄ ) = µ and var ( X̄ ) = σ 2/ n , where β 2is the variance of X . An estimator of a parameter is called unbiased if its mean is equal to the true value of the parameter. X̄ is a commonly used estimator of µ because it is unbiased and has a smaller variance for a larger sample size n .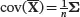 , where Σis the population covariance matrix of X. The population covariance matrix is defined shortly. The sample mean vector X̄is an unbiased estimator of the population mean vector μ.
, where Σis the population covariance matrix of X. The population covariance matrix is defined shortly. The sample mean vector X̄is an unbiased estimator of the population mean vector μ.