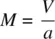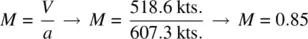Indicated airspeed (IAS) is the direct reading of the airspeed indicator, and is uncorrected for errors related to installation or nonstandard atmospheric density. If there are any errors in the instrument, they may be shown on an instrument error card located near the instrument and/or in the AFM.
Calibrated airspeed (CAS) is obtained when the necessary corrections have been made to the IAS for installation error and instrument error. These position errors are especially prevalent at lower airspeeds, and the IAS may be “indicating” slower than the CAS. Most of the time in non‐pressurized aircraft operating at lower altitudes, the CAS can be assumed to be within several knots of the IAS.
Equivalent airspeed (EAS) results when the CAS has been corrected for compressibility effects. Figure 2.12shows a compressibility correction chart. In general, if flying above 10 000 ft and 200 kts., the compressibility correction should be made. Unlike the instrument and position error charts, which vary with different aircraft, this chart is good for any aircraft.
EAS is not a significant factor in airspeed computations when aircraft fly at relatively low speeds and altitudes, but at higher speeds and altitudes, the compressibility correction must be taken into account. For example, if an aircraft is flying at a pressure altitude of 20 000 ft at a CAS of 400 kts., Figure 2.12indicates a compressibility correction of −17.5 kts. The EAS for this example is 382.5 kts.
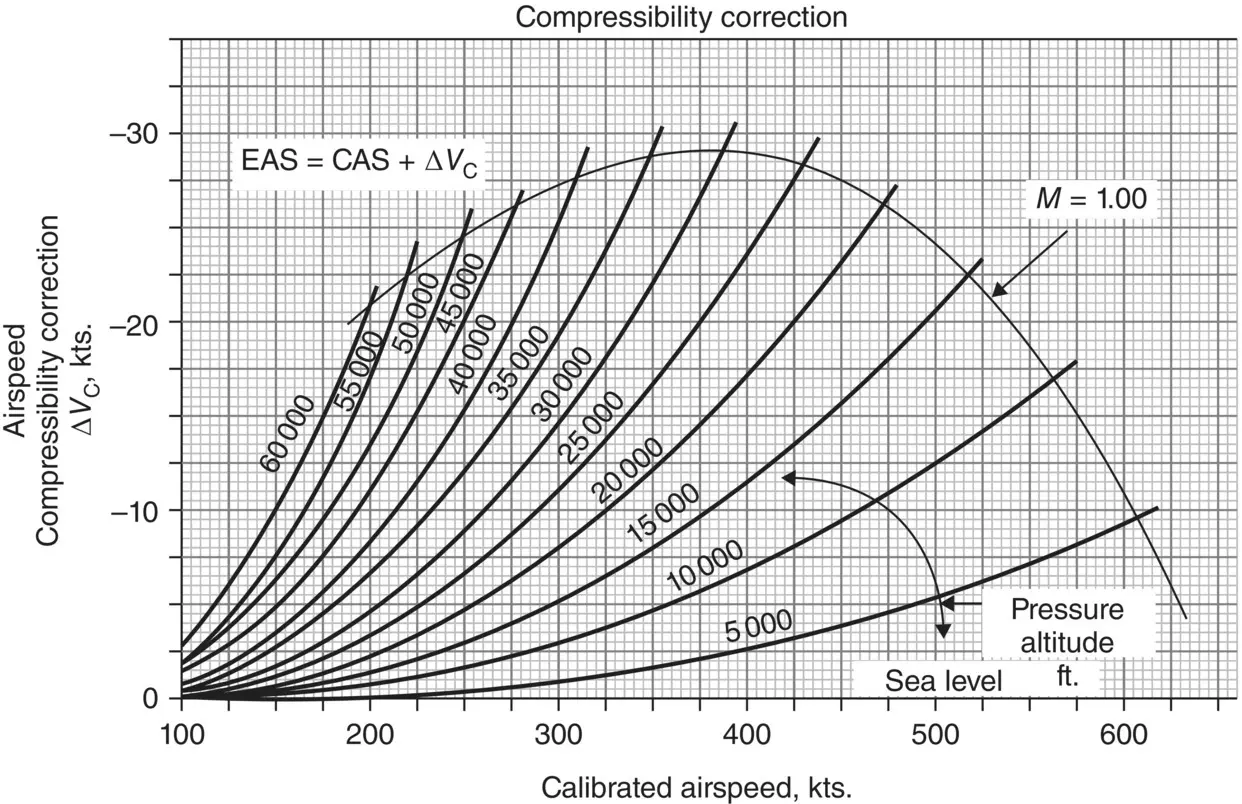
Figure 2.12 Compressibility correction chart.
True airspeed (TAS) is obtained when EAS has been corrected for density ratio, the airspeed indicator measures dynamic pressure and is calibrated for sea level standard day density. As altitude increases, the density ratio decreases and a correction must be made. The correction factor is 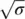 :
:
(2.12) 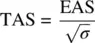
Values of 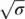 can be found in the ICAO Standard Altitude Chart ( Table 2.1); values of 1/
can be found in the ICAO Standard Altitude Chart ( Table 2.1); values of 1/ 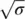 can be found in Figure 2.13.
can be found in Figure 2.13.
Due to the decrease in air density with an increase in altitude, for any given TAS, CAS will decrease as altitude increases. As higher altitudes are attained, the aircraft must fly faster to obtain the same pressure differential. For a given CAS, as an aircraft increases in altitude, the TAS will increase. The higher the aircraft travels in altitude, the greater the difference between CAS and TAS.
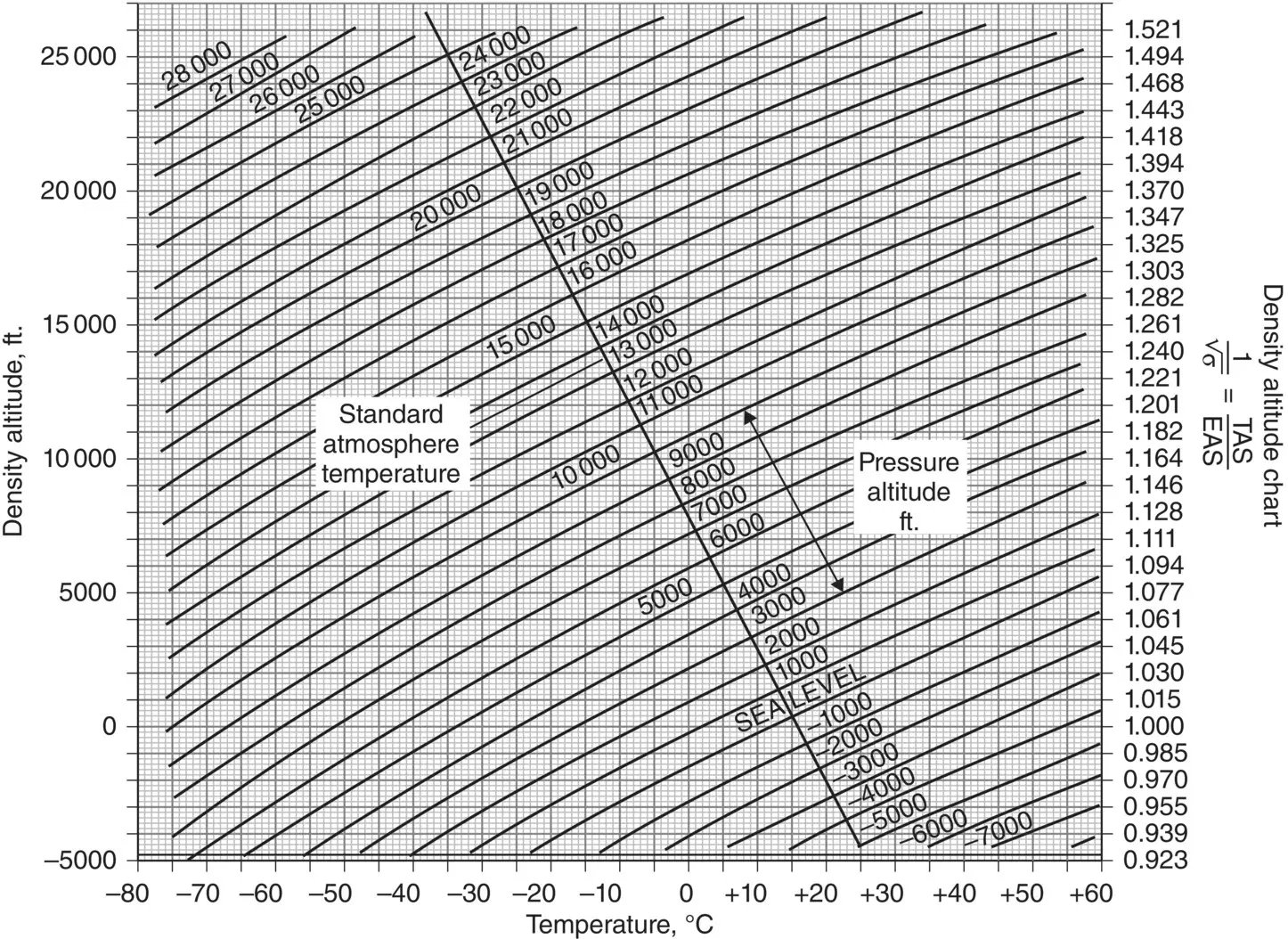
Figure 2.13 Altitude and EAS to TAS correction chart.
Using our example from the CAS discussion, EAS was determined to be 382.5 kts. If the outside air temperature at a pressure altitude of 20 000 ft is −30 °C, we can utilize Eq. 2.12to find the TAS. From Table 2.1, the pressure ratio ( δ ) is 0.4595.

Figure 2.14depicts the change in TAS between sea level and 15 000 ft when the IAS remains constant. For the respective IAS, the CAS calibration has been applied. As the aircraft climbs, the TAS increases as the air density decreases. The aircraft must travel at 130 kts. TAS to register 100 kts. on the airspeed indicator.
Understanding the relationship between the speeds above, and the calculation of each one, can be facilitated by remembering “ICE‐T.” I AS is read off the airspeed indicator, C AS is IAS corrected for installation/position errors, E AS is CAS corrected for compressibility, and finally T AS is EAS corrected for temperature and pressure.
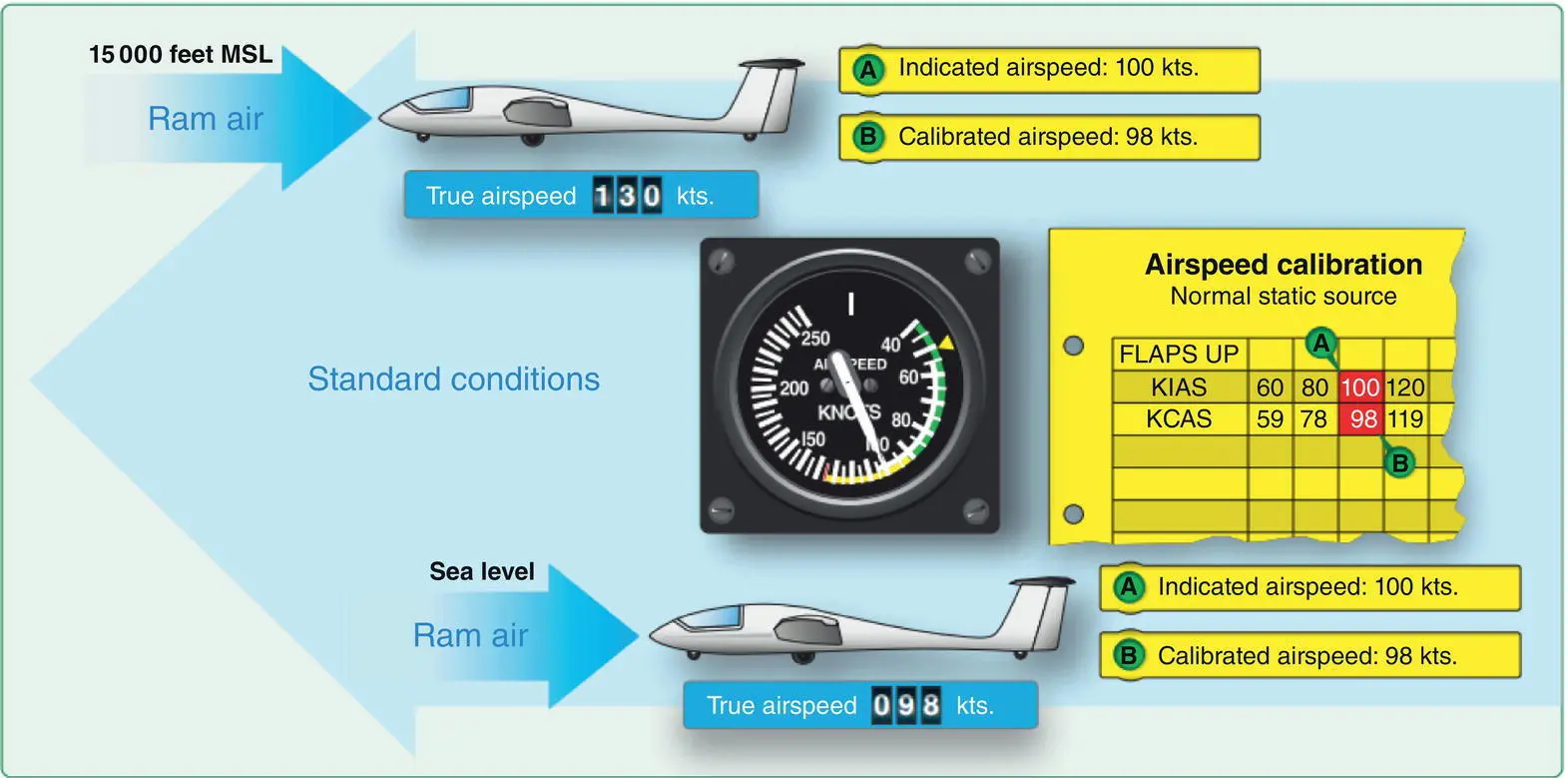
Figure 2.14 IAS, CAS, and TAS comparison.
Source: U.S. Department of Transportation Federal Aviation Administration (2013).
The Mach number is found by comparing TAS to the speed of sound for a given set of conditions at a specific altitude. The speed of sound is an important factor in the study of high‐speed flight and is discussed in depth in Chapter 14. Because the aircraft’s speed in relation to the speed of sound is so important in high‐speed flight, airspeeds are usually measured as Mach number (named after the Austrian physicist Ernst Mach). Mach number is the aircraft’s true airspeed divided by the speed of sound (in the same atmospheric conditions):
(2.13) 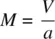
where
M = Mach number
V = true airspeed (kts.)
a = local speed of sound (kts.)
Using the TAS from the previous example (518.6 kts.), when a = 607.3 kts., calculate the Mach number for the aircraft.
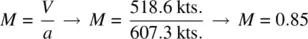
Groundspeed (GS) is the actual speed of the aircraft over the ground, either calculated manually or more commonly nowadays read off the GPS (Global Positioning Satellite) navigational unit. The GS increases with a tailwind and decreases with a headwind, and is TAS adjusted for the wind. Groundspeed equals true airspeed in a no wind situation. Consider an airplane that has departed an airport located at sea level, then lands on a runway located at 5000 ft. Even though the IAS on approach will remain the same as if the airplane was landing at sea level, the TAS (and GS) will be higher at the airport with the higher elevation, thus more runway will be utilized during the landing.
| a |
Speed of sound (local for a given condition) |
| A |
Area (ft 2) |
| AGL |
Above ground level |
| CAS |
Calibrated airspeed (kts.) |
| °C |
Celsius temperature (°) |
| DA |
Density altitude |
| EAS |
Equivalent airspeed |
| °F |
Fahrenheit temperature |
| GS |
Groundspeed |
| H |
Total pressure(head) (psf) |
| IAS |
Indicated airspeed |
| °K |
Kelvin temperature |
| MSL |
Mean sea level |
| M |
Mach number (ratio) |
| P |
Static pressure |
| PA |
Pressure altitude |
| P 0 |
Sea level standard pressure |
| q |
Dynamic pressure |
| R |
Universal gas constant |
| °R |
Rankine temperature |
| TAS |
True airspeed |
| T |
Absolute temperature |
| T 0 |
Sea level standard temperature |
| V |
Velocity (fps) |
| V k |
Velocity (kts.) |
| δ (delta) |
Pressure ratio |
| θ (theta) |
Temperature ratio |
| ρ (rho) |
Density |
| σ (sigma) |
Density ratio |
Читать дальше


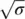 :
: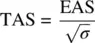
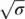 can be found in the ICAO Standard Altitude Chart ( Table 2.1); values of 1/
can be found in the ICAO Standard Altitude Chart ( Table 2.1); values of 1/ 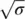 can be found in Figure 2.13.
can be found in Figure 2.13.