Joseph R. Badick - Flight Theory and Aerodynamics

Regarding aircraft performance, two types of altitude are of most interest to a pilot: pressure altitude and density altitude.

Pressure altitude is that corrected altitude in the standard atmosphere corresponding to a certain static pressure. Pressure altitude is the vertical distance above a standard datum plane where atmospheric pressure is 29.92″. In the United States, at FL180 and above, the altimeter is always set to 29.92″ unless abnormally low pressure exists in the area. Pressure altitude is used in performance calculations to compute true airspeed, density altitude, and takeoff and landing data.

Figure 2.3provides a convenient method to determine pressure altitude. For example, if a given airport elevation is 3500 ft and the automated weather observation states a pressure value of 30.10″, use the altitude correction column to determine that 165 needs to be subtracted from 3500 ft. The pressure altitude in the given condition is 3335 ft, which makes sense as it is lower. The pressure given is higher than standard pressure, thus the air density is higher, resulting in a lower pressure altitude.

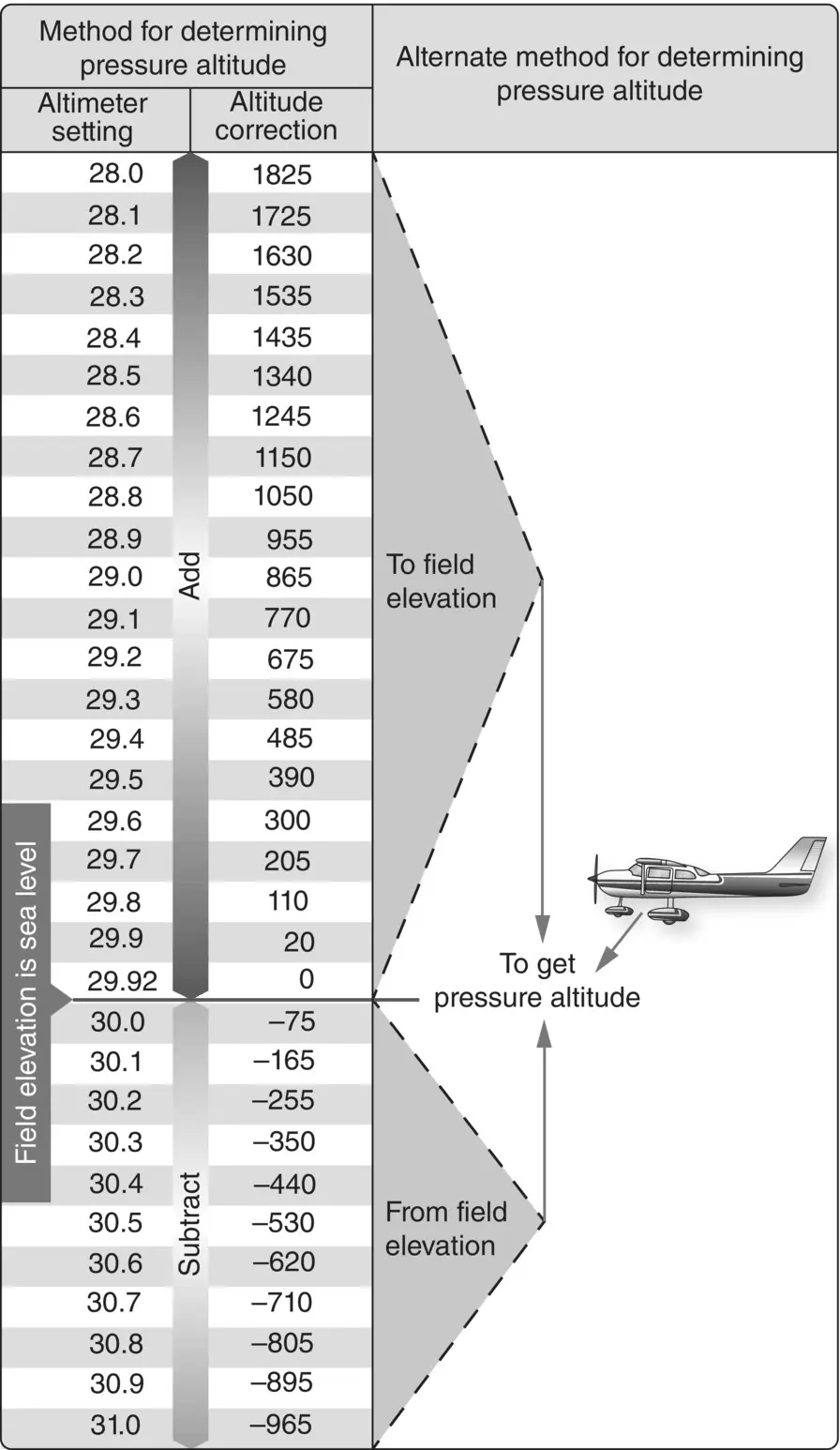
Figure 2.3 Field elevation versus pressure altitude.

Source: U.S. Department of Transportation Federal Aviation Administration (2008a).

Density altitude is the altitude used to calculate aircraft performance in most situations. Density altitude is found by correcting pressure altitude for nonstandard temperature conditions. Pressure altitude and density altitude are the same when conditions are standard. Once pressure altitude has been determined, the density altitude is calculated using outside air temperature. If the temperature is below standard, then the density altitude is lower than pressure altitude and aircraft performance is improved. If the outside air temperature is warmer than standard, the density altitude is higher than pressure altitude and aircraft performance is degraded.

Figure 2.4is a commonly used chart for performance calculations to determine density altitude. As provided by the Pilot’s Handbook of Aeronautical Knowledge , using Figure 2.4, we will calculate the pressure altitude first, and then calculate the resulting density altitude based on temperature. With a given airport elevation of 5883 ft and an altimeter setting of 30.10″, as shown in Figure 2.3the resulting pressure altitude is calculated to be 5718 ft. Since the density altitude is pressure altitude corrected for nonstandard temperature, we then use the provided 70 °C temperature and move from the X ‐axis vertically until we reach the diagonal line (interpolated) for 5718 ft. Moving horizontally to the Y ‐axis, the density altitude is determined to be 7700 ft, which makes sense as it is higher than the pressure altitude since the temperature is above standard for that altitude, resulting in lower air density (higher density altitude).

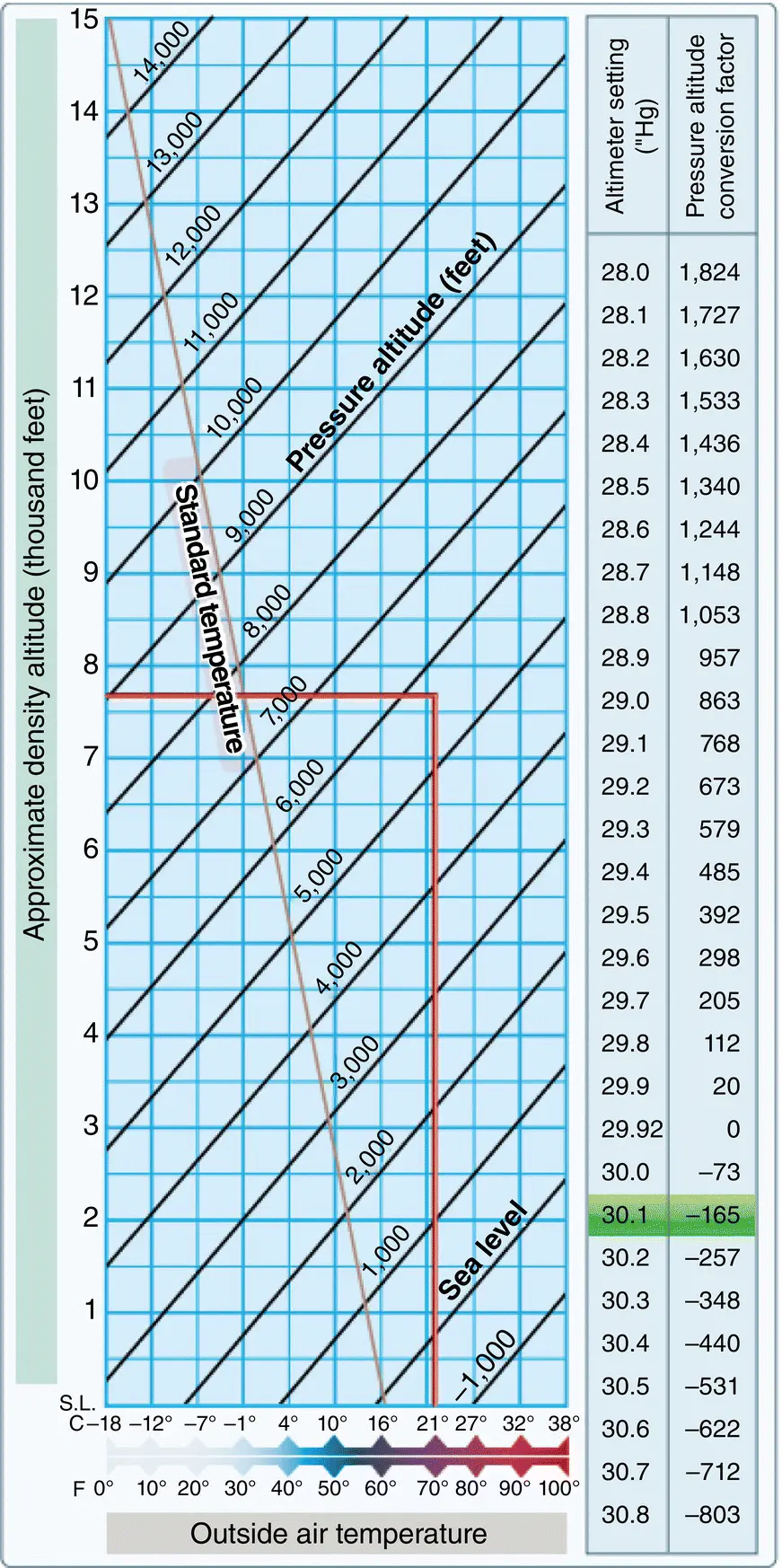
Figure 2.4 Pressure altitude conversion and density altitude chart.

Source: U.S. Department of Transportation Federal Aviation Administration (2016b).

Using Table 2.1and several of the equations from earlier in this chapter, the density altitude can also be determined using ratios. An aircraft at an indicated altitude of 1800 ft has an altimeter setting of 29.70″ Hg (sea level) and an outside air temperature of 75 °F. Calculate the density altitude:

Pressure altitude (P.A.) = 2005 ft is found using Figure 2.3.

Referencing Table 2.1for P.A. 2000 ft, δ = 0.9298

Using Eq. 2.2, θ = 1.031

Using Eq. 2.5, solve for the density ratio

Using Table 2.1, it can be interpolated that with a density ratio of 0.902, the resultant density altitude is 3500 ft. This makes sense as the sea level pressure is lower than standard and the temperature is above standard for that altitude, which results in lower air density (higher density altitude).As discussed, density altitude influences aircraft performance; the higher the density altitude, the lower the aircraft performance. So, in the previous problem, even though the aircraft is at an indicated altitude of 1800 ft, the density altitude for performance calculations is 3500 ft. Low air density equals a higher density altitude; high air density equals a lower density altitude. Therefore, aircraft performance charts are provided for various density altitudes.

A non‐pressurized, single‐engine aircraft departs for a cross‐country flight at 6500 ft. A portion of the route crosses rising terrain with peaks at 5000 ft. The pilot is only concerned with maintaining an indicated altitude of 6500 ft as filed on the visual flight rules (VFR) flight plan.

What other altitudes must the pilot consider along the route of flight? What are the implications of failing to adjust the altimeter setting if the barometric pressure is decreasing along the route? Consider the FAA definition of Maximum Elevation Figure (MEF) on VFR Sectionals and if nonstandard pressure and temperature may impact obstacle clearance.

Consider the flow of air through a pipe of varying cross section as shown in Figure 2.5. There is no flow through the sides of the pipe: air flows only through the ends. The mass of air entering the pipe, in a given unit of time, equals the mass of air leaving the pipe, in the same unit of time. The mass flow through the pipe, must remain constant. The mass flow at each station is equal. Constant mass flow is called steady‐state flow . The mass airflow is equal to the volume of air multiplied by the density of the air. The volume of air, at any station, is equal to the velocity of the air multiplied by the cross‐sectional area of that station.

The mass airflow symbol Q is the product of the density, the area, and the velocity:

(2.6)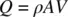

The continuity equation states that the mass airflow is a constant:

(2.7)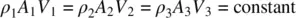

The continuity equation is valid for steady‐state flow, both in subsonic and supersonic flow. For subsonic flow, the air is considered to be incompressible, and its density remains constant. The density symbols can then be eliminated; thus, for subsonic flow,

(2.8)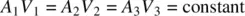

Velocity is inversely proportional to cross‐sectional area: as cross‐sectional area decreases, velocity increases.

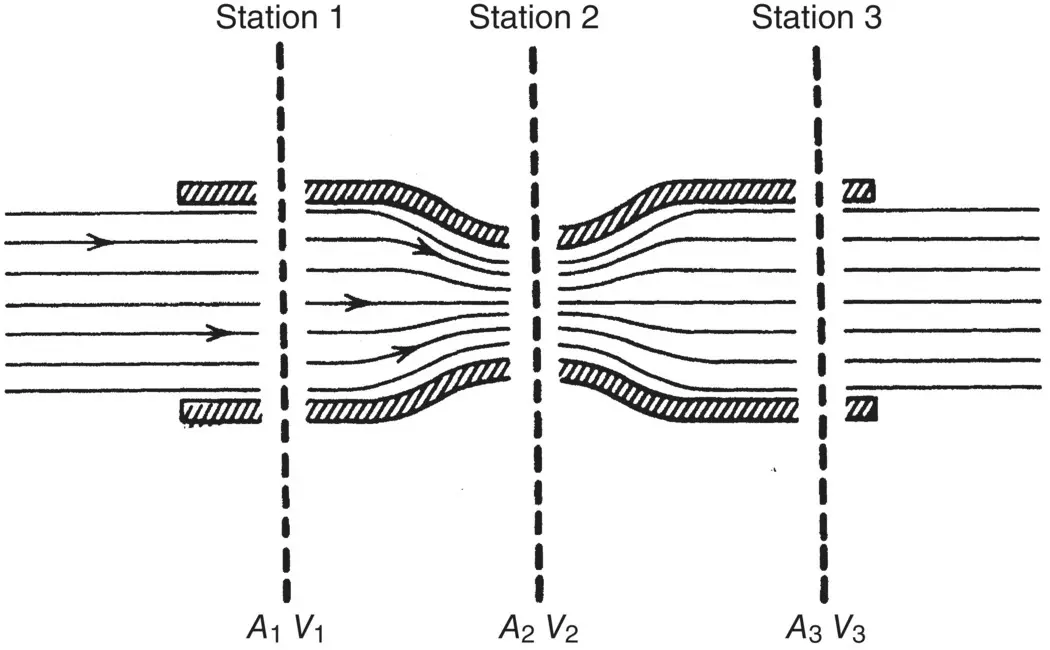
Figure 2.5 Flow of air through a pipe.

The continuity equation explains the relationship between velocity and cross‐sectional area. It does not explain differences in static pressure of the air passing through a pipe of varying cross sections. Bernoulli, using the principle of conservation of energy, developed a concept that explains the behavior of pressures in flowing gases.