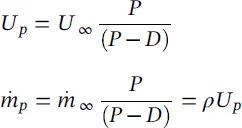1 ...7 8 9 11 12 13 ...20
2.1.2 Scope of a Vibration Analysis
A heat exchanger vibration analysis consists of the following steps: 1) flow distribution calculations, 2) dynamic parameter evaluation (i.e., damping, effective tube mass, and dynamic stiffness), 3) formulation of vibration excitation mechanisms, 4) vibration response prediction, and 5) resulting damage assessment (i.e., comparison against allowables). The requirements applicable to each step are outlined in this overview. Each step is discussed in more detail in the following chapters of this handbook.
Flow‐induced vibration problems usually occur on a small number of vulnerable tubes in specific areas of a component (e.g., piping elements, entrance regions and tube‐free lanes in heat exchangers, and U‐tubes in nuclear steam generators). Thus, a flow analysis is required to obtain the local flow conditions throughout these heat exchange components. Flow considerations are discussed in detail in Chapter 3.
2.2.1 Flow Parameter Definition
The end results of a flow analysis are the shell‐side cross‐flow velocity, U p, and fluid density, ρ , distributions along critical tubes. For flow‐induced vibration analyses, flow velocity is defined in terms of the pitch velocity:
(2‐1) 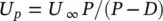
where U ∞is the free stream velocity (i.e., the velocity that would prevail if the tubes were removed), P is the pitch between the tubes and D is the tube diameter. For finned tubes, the equivalent or effective diameter, D eff, is used. The pitch velocity is sometimes called the reference gap velocity. The pitch velocity is a convenient definition since it applies to all bundle configurations.
The situation is somewhat more complex in two‐phase flow. Another parameter, steam quality or void fraction, is required to define the flow conditions. Two‐phase mixtures are rarely homogeneous or uniform across a flow path. However, it is convenient and simple to use homogeneous two‐phase mixture properties as they are well defined. This is done consistently here for both specifying vibration guidelines and formulating vibration mechanisms. The homogeneous void fraction, ε g, is defined in terms of the volume flow rates of gas, 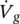 , and liquid,
, and liquid, 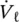 as:
as:
(2‐2) 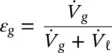
The homogeneous density, ρ , the free stream velocity, U ∞, and the free stream mass flux, 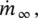 are defined using the homogeneous void fraction:
are defined using the homogeneous void fraction:
(2‐3) 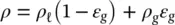
(2‐4) 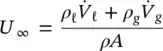
(2‐5) 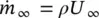
where ρg and ρℓ are the densities of the gas and liquid phase, respectively, and A is the free‐stream flow path area.
For both liquid and two‐phase cross flow, the pitch velocity, U p, and the pitch mass flux, 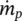 , are similarly defined as:
, are similarly defined as:
(2‐6) 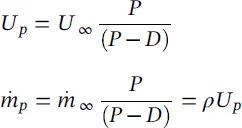
2.2.2 Simple Flow Path Approach
For relatively simple components, where the flow paths are reasonably well defined, a flow path approach may be adequate to calculate flow velocities, as illustrated in Fig. 2-1. In the flow path analysis approach, characteristic flow paths (i.e., through the tube bundle, between the tube bundle and shell, etc.) between regions of common pressures are identified. Flow impedances (i.e., pressure drop coefficients) are estimated. The flows within each path are then calculated. The resulting flow velocity distributions are then used to estimate vibration excitation mechanisms and predict vibration response.
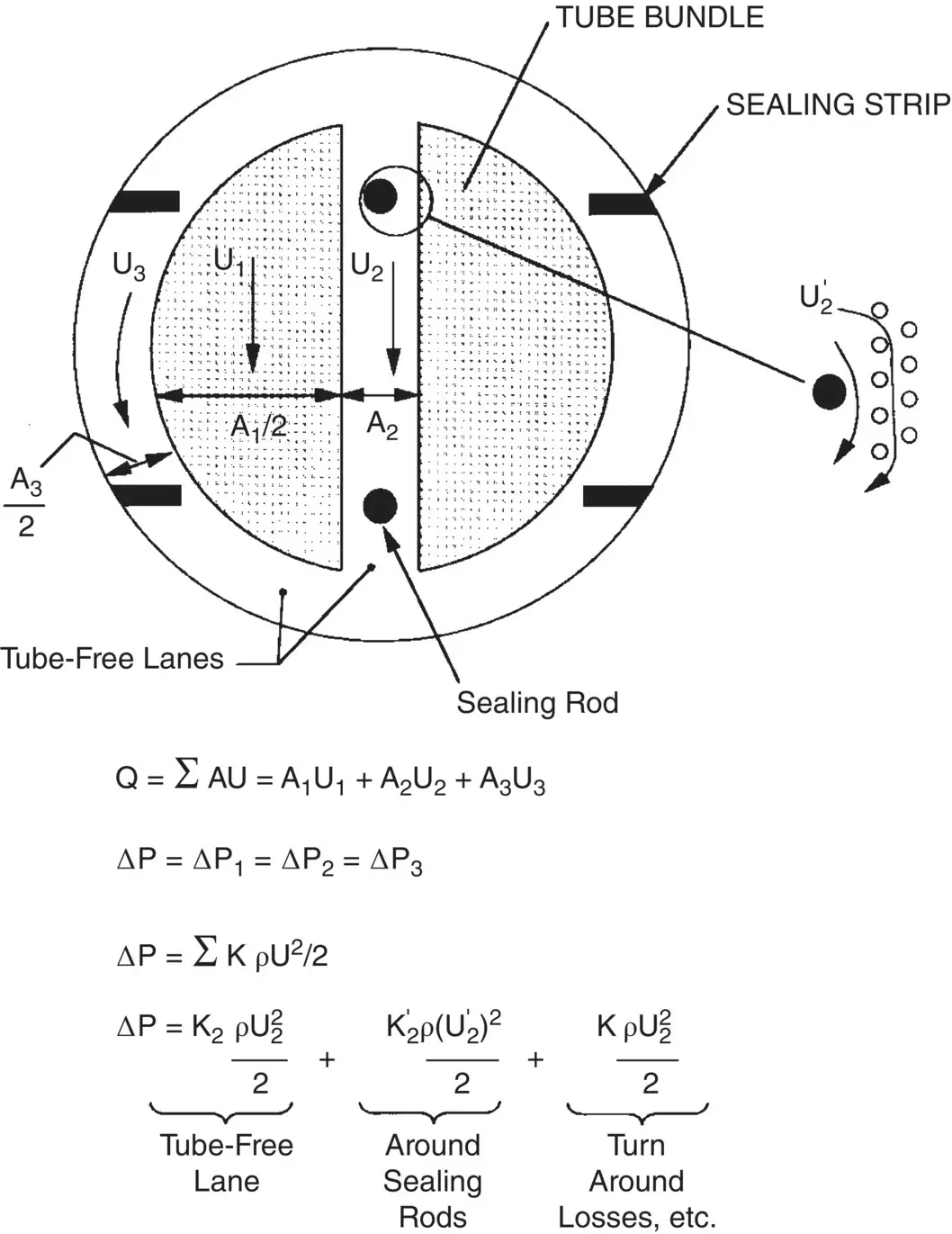
Fig. 2-1 Flow‐Path Approach.
All typical operating conditions must be considered including the following: 1) as‐designed operating conditions, from zero to 100% flow, 2) operating conditions with fouling of the tubes or crudding of the tube supports, and 3) other possible operating conditions (e.g., after chemical cleaning, system testing, etc.).
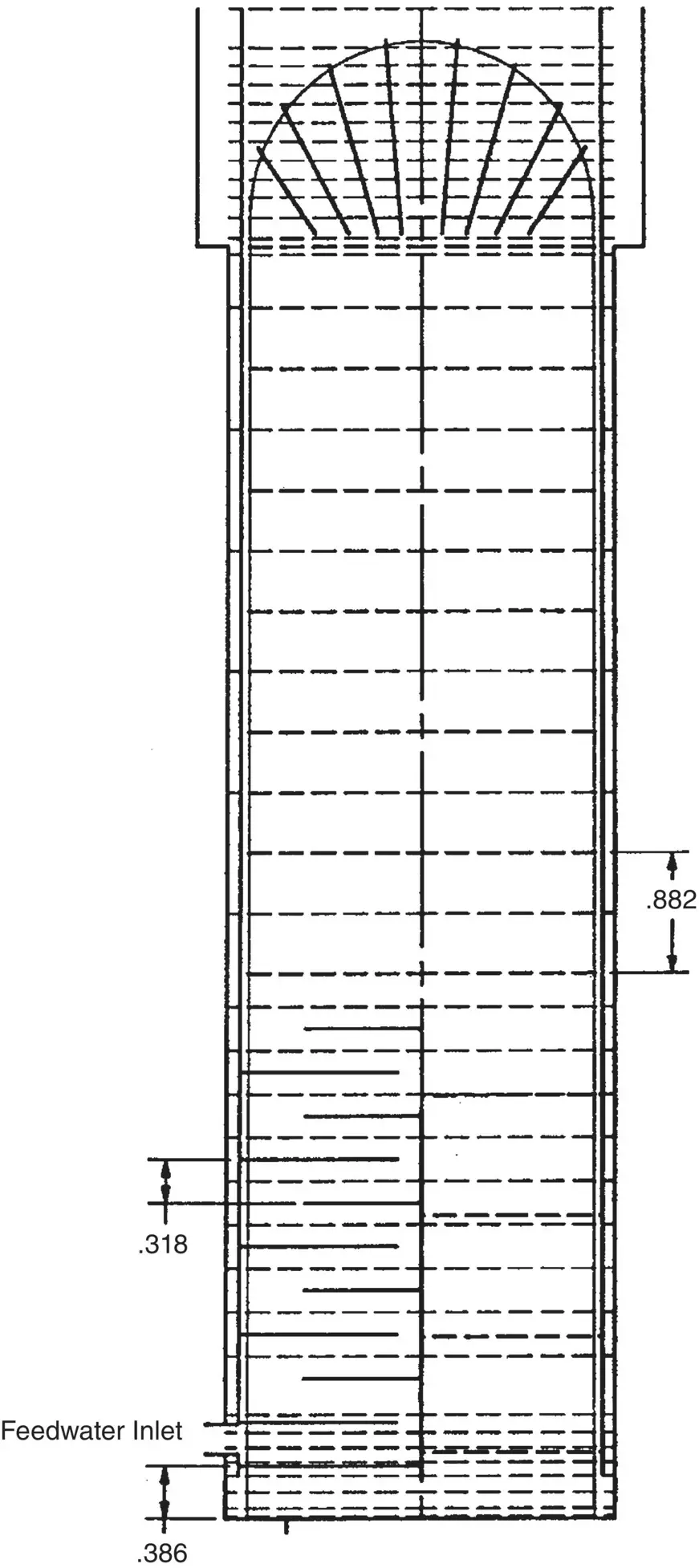
Fig. 2-2 Thermalhydraulic Analysis: Axial Grid Layout for a Typical Steam Generator with Preheater (Distances in Metres).
2.2.3 Comprehensive 3‐D Approach
For complex components such as nuclear steam generators and power condensers, a comprehensive three‐dimensional thermalhydraulic analysis is required. In such analyses, the component is divided into a large number of control volumes. The equations of energy, momentum and continuity are solved for each control volume. This is done with numerical methods using a computer code such as the THIRST code for steam generators (Pietralik, 1995). The numerical grid outlining the control volumes for the analysis of a typical steam generator is shown in Fig. 2-2. The grid must be sufficiently fine to accurately predict the flow distribution along the tube. Some typical thermalhydraulic analysis results are shown in Fig. 2-3for the U‐bend region of a steam generator. For flow‐induced vibration analyses, the results must be in the form of pitch flow velocity and fluid density distributions along a given tube. These distributions constitute the input to a flow‐induced vibration analysis of this particular tube. Figure 2-4shows pitch flow velocity and fluid density distributions for an example condenser tube.
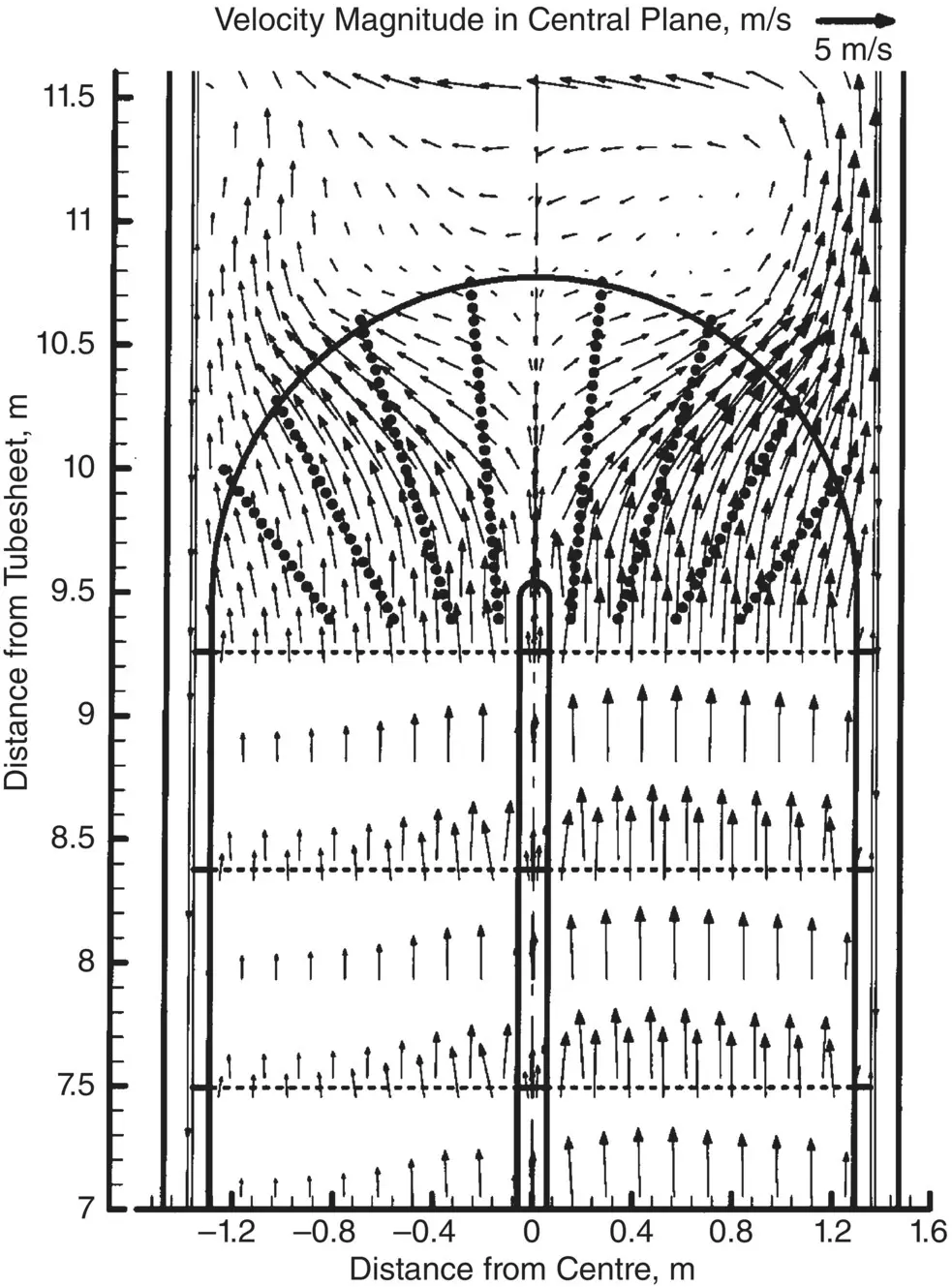
Fig. 2-3 Flow Velocity Vectors in the Central Plane of a Typical Steam Generator U‐Bend Region.
Читать дальше

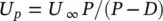
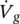 , and liquid,
, and liquid, 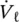 as:
as: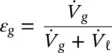
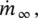 are defined using the homogeneous void fraction:
are defined using the homogeneous void fraction: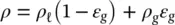
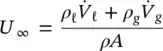
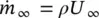
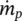 , are similarly defined as:
, are similarly defined as: