Cumrun Vafa - Das Universum in Rätseln

Die Quantenmechanik hatte anfangs nur einen begrenzten Anwendungsbereich. Er erforderte eine Neuformulierung, um sie in Einklang mit Maxwells Feldtheorie der elektrischen und magnetischen Kräfte zu bringen. Diese Neuformulierung war das Werk von Richard Feynman und anderen, die sich dabei an dem Ansatz orientierten, den schon Euler und Lagrange bei ihren Neuformulierungen der newtonschen Mechanik verfolgt hatten und dem wir nun ebenfalls folgen wollen.

In der klassischen Mechanik folgen Teilchen wie beschrieben denjenigen Wegen, für die die Wirkung minimal wird. Die Quantenfeldtheorie präsentiert eine kompliziertere Sichtweise – hier folgt ein Teilchen nicht nur einem einzigen Weg, sondern es nimmt alle denkbaren Wege, wobei jedem dieser Wege eine Phase (eine komplexe Zahl mit dem Betrag eins) zugeordnet ist. Die Wahrscheinlichkeit, dass ein Teilchen von einem beliebigen Anfangspunkt zu einem beliebigen Endpunkt gelangt, ist proportional zur Summe der Phasen aller möglichen Wege. Im Folgenden werden wir dies etwas formeller ausdrücken. (Sie können diesen Abschnitt gerne auch überspringen.)

Richard Feynmans Neuformulierung der Quantenmechanik mithilfe von Pfadintegralen postuliert, dass ein Teilchen zwischen den Punkten ( x 1, t 1) und ( x 2, t 2) verschiedenen Wegen folgt, die mit einem Exponentialterm mit der Wirkung im Exponenten gewichtet sind,

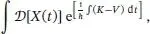
wobei ℏ die plancksche Konstante ist und die Integration über den Raum aller möglichen Wege zwischen ( x 1, t 1) und ( x 2, t 2) erfolgt. Das Integral ist eine komplexe Zahl, deren Betragsquadrat die Wahrscheinlichkeit angibt, dass ein Teilchen sich vom Ort x 1zur Zeit t 1an den Ort x 2zur Zeit t 2bewegt. Die klassischen Bahnen entsprechen dem Grenzfall ℏ → 0. In diesem Grenzfall liefert die Methode der stationären Phase zur Bestimmung des Integrals in guter Näherung diejenigen Wege, die bezüglich einer Variation des Wegs einem Extremum entsprechen – d. h., man erhält die klassischen Bahnen. Feynmans Neuformulierung der schrödingerschen Quantenmechanik ergab eine Theorie, die der Euler-Lagrange-Neuformulierung der newtonschen Mechanik im Sinn des Wirkungsprinzips ähnelt. Die Euler-Lagrange-Form der Mechanik passte von ihrer Struktur her gut zur Quantenmechanik (im Gegensatz zu Newtons ursprünglicher Formulierung), weshalb sie heute als grundlegender angesehen wird.

Die mathematische Formulierung der Quantenmechanik anhand von Pfadintegralen enthält ein unendlichdimensionales Integral, da der Raum aller möglichen Wege unendlich viele Dimensionen hat. Dennoch lässt sich dies mathematisch prä- zise formulieren. Denselben Pfadintegralansatz wandte Feynman auch auf Maxwells Theorie des Elektromagnetismus an, indem er über alle elektrischen und magnetischen Felder integrierte. Hierzu war eine Integration über den unendlichdimensionalen Raum der Funktionen auf R 4erforderlich, was in seiner mathematischen Komplexität noch weit über die (ebenfalls nicht ganz triviale) Integration über den unendlichdimensionalen Raum der Wege hinausgeht.

Dies ist ein zentrales Thema der Quantenfeldtheorie, deren mathematische Untermauerung rund 70 Jahre nach ihrer ursprünglichen Formulierung immer noch im Gang ist! Obwohl es immer noch keine mathematisch strenge Formulierung einer Quantenfeldtheorie gibt, haben Physiker eine Reihe von Rechenwerkzeugen (darunter verschiedene Näherungsverfahren) entwickelt, deren Ergebnisse mit fantastischer Genauigkeit mit den verfügbaren Experimenten übereinstimmen.

Frühe Versuche, die allgemeine Relativitätstheorie aufbauend auf Feynmans Theorie mit der Quantenfeldtheorie zu einer vereinheitlichten Theorie der Quantengravitation zusammenzuführen, die die Gravitation auf der Ebene einzelner Teilchen beschreiben konnte, waren nicht von Erfolg gekrönt. Rechenverfahren, die für die Quantenfeldtheorie entwickelt worden waren, liefern für Wahrscheinlichkeitsamplituden, bei denen Quantenaspekte der Gravitation eine Rolle spielen – wie die Streuung zweier Quanten von Gravitationswellen (zweier ,,Gravitonen“), die aufeinandertreffen – unter bestimmten Umständen unendlich große Zahlen. Das ist ein ernstes Problem, denn eine Wahrscheinlichkeit, die größer als eins werden kann – geschweige denn unendlich groß –, ist als Konzept bedeutungslos.

Selbst wenn wir eine konsistente Quantentheorie der Schwerkraft hätten, würde die Bestätigung (oder Widerlegung) einer solchen Theorie unsere derzeitigen experimentellen Mittel bei Weitem übersteigen, da dies Kollisionsenergien erfordern würde, die alles, was in Labors auch nur annähernd realisierbar wäre, um viele Grö- ßenordnungen übersteigen würde. Manche Physiker zögerten daher, überhaupt an Theorien der Quantengravitation zu arbeiten, weil deren experimentelle Überprüfung so unwahrscheinlich war und alle Versuche, die Quantenmechanik mit der allgemeinen Relativitätstheorie zu vereinen, zu unsinnigen Ergebnissen zu führen schienen. Andererseits wissen Physiker aus der Erfahrung der Entdeckungen von Maxwell, Dirac und anderen aber auch, dass ein scheinbarer Widerspruch nicht nur ein Grund für Kopfschmerzen, sondern auch ein Geschenk sein kann – eine Chance für einen Durchbruch – und dass die Überwindung eines solchen Widerspruchs die Physik schon oft entscheidend vorangebracht hat. Aus diesem Grund werden Physiker nicht müde, diese Inkonsistenz aufzulösen – immer in der Hoffnung, am Ende zu einer tragfähigen, einheitlichen Theorie zu gelangen.

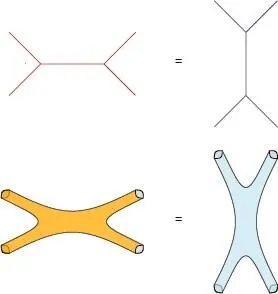
Abb. 1.7 Die String-Streudiagramme der beiden ungleichen Streuprozesse besitzen dieselbe Topologie.

Eine mögliche Lösung kam aus einer ganz unerwarteten Richtung. In den späten 1960er-Jahren grübelten die Physiker verwirrt über die Ergebnisse von Experimenten zur Streuung subatomarer Teilchen, der sogenannten Hadronen. Sie betrachteten zwei Arten von Prozessen. Im ersten Fall gab ein Teilchen etwas ab, das von einem zweiten Teilchen absorbiert wurde. Im zweiten Fall verschmolzen zwei Teilchen zu einem einzigen, bevor sie sich wieder in zwei Teilchen teilten (siehe Abb. 1.7). Obwohl beide Prozesse recht unterschiedlich zu sein schienen, führten sie zu denselben Ergebnissen. Die Physiker verstanden nicht, warum dies der Fall war, vermuteten aber, dass sie einer neuen Art von Symmetrie auf der Spur waren.

Später stellte sich heraus, dass diese Symmetrie offengelegt werden konnte – sodass die beiden scheinbar unterschiedlichen physikalischen Prozesse als identisch aufgefasst werden konnten –, wenn man die punktförmigen Teilchen in den ursprünglichen Modellen durch gestreckte, vibrierende Objekte ersetzte, die man als Strings bezeichnete. Ursprünglich wurden Strings als mathematische Objekte ohne tiefere physikalische Begründung eingeführt, aber die Vorstellung hat sich inzwischen durchgesetzt und erwies sich als recht fruchtbar. Dies war die Geburtsstunde der Stringtheorie – einer Theorie, in der Teilchen (Hadronen) als Grundbausteine der Natur durch Strings ersetzt wurden. Auf diese Weise erhielt die obige Symmetrie eine geometrische Interpretation: Wenn Strings sich bewegen, bilden sie Röhren, und wenn sie sich verbinden oder aufspalten, bilden sie Flächen. Die beiden Streukanäle entsprechen für Strings dem gleichen Diagramm, wodurch sich diese Symmetrie erklärt (siehe Abb. 1.7).