Cumrun Vafa - Das Universum in Rätseln

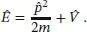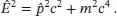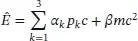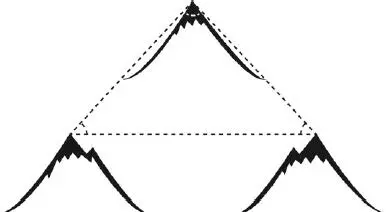
Abb. 1.5 Nach einer (unbestätigten) Legende soll Carl Friedrich Gauß versucht haben, die Krümmung des Raums zu messen, indem er die Winkel in einem Dreieck bestimmte, dessen Ecken durch den Brocken im Harz, den Inselsberg im Thüringer Wald und den Hohen Hagen bei Göttingen gebildet wurden. Der Gedanke war sicherlich einen Versuch wert, auch wenn er dabei keine Abweichung von den nach der euklidischen Geometrie erwarteten 180° beobachten konnte.

Dank Einsteins gut geprüfter Theorie wissen wir heute, dass das Universum tatsächlich gekrümmt ist. Wir wissen auch, dass Gauß zwar auf dem richtigen Weg war, dass aber die Krümmung, die er zu messen versuchte, für die ihm zur Verfügung stehenden experimentellen Mittel zu klein war. Riemann und Gauß waren Mathematiker, aber einige ihrer interessanten mathematischen Erkenntnisse fanden später über Einsteins allgemeine Relativitätstheorie ihren Weg in die Physik. Wir sehen hier ein weiteres Beispiel für die gegenseitige Unterstützung zwischen Physik und Mathematik, die beide Bereiche vorangebracht haben. Im Gegensatz zur speziellen Relativitätstheorie, bei der es um nahezu triviale Mathematik ging, war die Mathematik der allgemeinen Relativitätstheorie ausgesprochen komplex und anspruchsvoll. So radikal diese Ideen jedoch auch waren, die fast gleichzeitig aufkommende Quantenmechanik erschien vielen Wissenschaftlern noch weitaus rätselhafter und verwirrender. Das galt auch für Einstein, der mit dieser Theorie, für die er Pionierarbeit leistete, nie wirklich glücklich war.

Die Quantenmechanik war insofern eine Revolution, als sie die Physik auf Wahrscheinlichkeiten gründete. Viele Physiker fassten das als Rückschritt auf, da es implizierte, dass keine sicheren Vorhersagen mehr möglich waren, wie sich die Natur verhalten würde. Physikalische Systeme waren plötzlich zufälligen Schwankungen oder Fluktuationen unterworfen, was bedeutete, dass der Zufall und nicht die Gewissheit die Regel war. Hiergegen erhob Einstein seinen oft zitierten Einwand ,,Gott würfelt nicht.“ Die Quantenmechanik ist in der Tat in vielerlei Hinsicht kontraintuitiv, selbst für moderne Physiker. Das veranlasste Richard Feynman zu seiner ebenfalls berühmten Aussage: ,,Ich glaube sicher sagen zu können, dass niemand die Quantenmechanik versteht.“ Trotzdem ist die Quantenmechanik schon seit Langem ein unverrückbarer Grundpfeiler der Physik – aus dem einfachen Grund, weil sie mit den Experimenten außerordentlich gut übereinstimmt.

Das Aufeinandertreffen der Quantenmechanik mit den bis dahin etablierten Grundlagen der Physik führte zu einigen interessanten Rätseln. In den 1920er- Jahren stellten Physiker in Experimenten fest, dass Elektronen einen zusätzlichen ,,Freiheitsgrad“ – ein unabhängiges, bestimmendes Merkmal – zu besitzen schienen, das sie Spin nannten. Obwohl dieser Begriff einen Bezug zu der üblichen Bedeutung des Wortes (engl. to spin = sich drehen, rotieren) hatte, hatte er in diesem Fall doch eine viel grundlegendere Bedeutung.

Erwin Schrödinger hatte bereits eine Gleichung aufgestellt, die die Quantenmechanik von Teilchen bei Geschwindigkeiten beschrieb, die wesentlich kleiner als die Lichtgeschwindigkeit waren (die Schrödinger-Gleichung). Paul Dirac versuchte nun, die spezielle Relativitätstheorie mit der Quantenmechanik zu kombinieren, um auch Teilchen mit Geschwindigkeiten nahe der Lichtgeschwindigkeit beschreiben zu können. Dabei stellte er fest, dass er hierfür einen zusätzlichen Freiheitsgrad benötigte und lieferte so eine Erklärung für den Ursprung dieser neuen Eigenschaft. Wieder griff die Mathematik ein, um zwei Gebiete der Physik miteinander in Einklang zu bringen, und dies eröffnete, wie wir im Folgenden sehen werden, neue Wege in der Physik.

Um die Situation besser verstehen zu können, wollen wir zunächst einen Blick auf die nichtrelativistische Schrödinger-Gleichung werfen 4) :

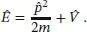
Diracs Ziel war jedoch eine Gleichung, die in Einklang mit Einsteins bekannter Gleichung aus der speziellen Relativitätstheorie stehen und dieselbe Form wie diese haben sollte:

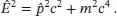
Damit seine Gleichung außerdem auch die Form der Schrödinger-Gleichung hatte, wollte Dirac die Potenz von E in der obigen Gleichung von E 2auf E reduzieren, ohne dabei aber die Quadratwurzel zu ziehen. Er erkannte, dass er dies erreichen konnte, indem er 4 × 4-Matrizen für seine Gleichung verwendete, weshalb er vier Matrizen a k und 𝛽 einführte, sodass die Gleichung erfüllt war. Es zeigte sich, dass aus dem Quadrat dieser Beziehung bei geeigneter Wahl der Matrizen die einsteinsche Relation entstand. Außerdem lieferten dieselben Matrizen auch den zusätzlichen Freiheitsgrad des Elektronenspins. So führte eine mathematische Idee Dirac zu einer erfolgreichen Erklärung für den Ursprung des Elektronenspins, was wiederum veranschaulicht, wie abstrakte Mathematik zu konkreten physikalischen Erkenntnissen führen kann. Die Dirac-Gleichung ist eine der berühmtesten Aussagen nicht nur der Physik, sondern auch der Mathematik und wird seither von Wissenschaftlern beider Disziplinen untersucht.

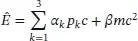
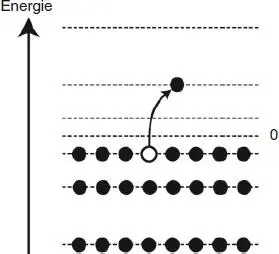
Abb. 1.6 Die Dirac-Gleichung lieferte Lösungen mit sowohl positiven als auch negativen Energien. Dirac versuchte dies zu erklären, indem er argumentierte, dass die negativen Energiezustände mit einem „Dirac-See“ von Elektronen gefüllt seien. Wenn eines der Elektronen aus dem „See“ in einen positiven Energiezustand springt, hinterlässt es ein Loch – ein Teilchen mit positiver Ladung, das ansonsten mit dem Elektron identisch ist.

Wolfgang Pauli wies jedoch bald darauf hin, dass Diracs Gleichung beliebige negative Energiezustände zulässt. Dirac akzeptierte dies als gravierendes Problem, das es zu lösen galt. 5) Er versuchte eine Lösung zu finden, indem er Paulis Ausschlussprinzip anwendete, welches besagt, dass keine zwei Elektronen dieselbe Umlaufbahn teilen können. Dirac schlug vor, dass die Bahnen, die negativen Energien entsprechen, bereits besetzt seien (siehe Abb. 1.6). Die Gruppe dieser Teilchen mit negativer Energie wurde als ,,Dirac-See“ 6) bezeichnet. Wenn diese Zustände alle besetzt waren, konnte folglich kein anderes Elektron auf die Bahnen negativer Energie geraten, womit das Problem gelöst war!

Die Physiker stellten jedoch fest, dass diese Idee die seltsame Möglichkeit aufwarf, dass Teilchen aus dem See in einen höheren Energiezustand angeregt werden könnten, wodurch ein Loch mit einer positiven Ladung desselben Betrags wie die Ladung des Elektrons zurückbliebe, das sich wie ein neues Teilchen mit einer Ladung entgegengesetzt zu der des Elektrons verhielte. Dirac versuchte zunächst, dieses neue Problem zu ignorieren, indem er behauptete, das neue Teilchen mit positiver Ladung sei nichts anderes als ein Proton. Andere Physiker wiesen jedoch bald darauf hin, dass das positiv geladene Teilchen nach der Dirac-Gleichung dieselbe Masse wie das Elektron haben müsse, das Proton aber etwa 2000-mal schwerer als das Elektron sei. Schließlich musste Dirac akzeptieren, dass seine Gleichung die Existenz eines positiv geladenen Teilchens mit der Masse eines Elektrons implizierte, das später als Antiteilchen des Elektrons bezeichnet wurde. Da von der Existenz eines solchen Teilchens nichts bekannt war, geriet Diracs Theorie ernsthaft in Zweifel. Selbst Dirac wurde im Hinblick auf diesen Aspekt seiner Gleichung immer schweigsamer. Es dauerte jedoch nicht lange, bis Carl Anderson bei einer Untersuchung der kosmischen Strahlung in seiner Teilchenkammer experimentelle Beweise für dieses Teilchen entdeckte, das daraufhin als Positron bezeichnet wurde. Tatsächlich hatte das Positron bis auf das Vorzeichen seiner Ladung genau dieselben Eigenschaften wie das Elektron. Wieder führte mathematische Eleganz zur Vorhersage neuer physikalischer Erkenntnisse, die zunächst unglaublich erschienen, sich aber schließlich doch als zutreffend erwiesen.