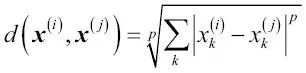Vahid Mirjalili - Python Machine Learning

1.Elige el número de k y una medida de distancia.

2.Encuentra los k-vecinos más cercanos de la muestra que quieres clasificar.

3.Asigna la etiqueta de clase por mayoría de votos.

La siguiente imagen muestra cómo se ha asignado un nuevo punto de datos (?) a la etiqueta de clase triángulo por mayoría de votos entre sus cinco vecinos más cercanos.

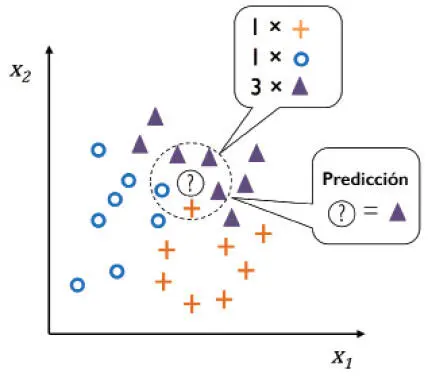
Basado en la medida de distancia seleccionada, el algoritmo KNN encuentra en el con-junto de datos de entrenamiento las muestras k que están más cerca (son más similares) del punto que queremos clasificar. A continuación, la etiqueta de clase del nuevo punto de datos se determinada por mayoría de votos entre sus k vecinos más cercanos.

La principal ventaja de un enfoque basado en memoria como este es que el clasificador se adapta inmediatamente cuando recogemos nuevos datos de entrenamiento. Sin embargo, la cara oculta es que, en el peor de los casos, la complejidad computacional para la clasificación de nuevas muestras crece linealmente con el número de muestras en el conjunto de datos de entrenamiento –a menos que el conjunto de datos tenga muy pocas dimensiones (características) y el algoritmo haya sido implementado mediante estructuras de datos eficientes, como los árboles kd–. An Algorithm for Finding Best Matches in Logarithmic Expected Time, J. H. Friedman, J. L. Bentley, y R.A. Finkel, ACM transactions on mathematical software (TOMS), 3(3): 209–226, 1977. Además, no podemos descartar muestras de entrenamiento puesto que no existe ningún paso de entrenamiento involucrado. Por tanto, el espacio de almacenamiento puede llegar a ser un desafío si estamos trabajando con grandes conjuntos de datos.

Con la ejecución del siguiente código, implementaremos un modelo KNN en scikit-learn mediante una distancia euclidiana:

>>> from sklearn.neighbors import KNeighborsClassifier

>>> knn = KNeighborsClassifier(n_neighbors=5, p=2,

... metric='minkowski')

>>> knn.fit(X_train_std, y_train)

>>> plot_decision_regions(X_combined_std, y_combined,

... classifier=knn, test_idx=range(105,150))

>>> plt.xlabel('petal length [standardized]')

>>> plt.ylabel('petal width [standardized]')

>>> plt.legend(loc='upper left')

>>> plt.show()

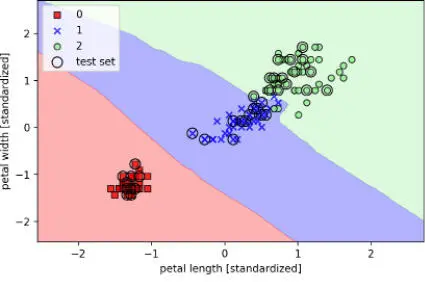
Al especificar cinco vecinos en el modelo KNN para este conjunto de datos, obtenemos un límite de decisión relativamente suave, como se muestra en la siguiente imagen:

En caso de empate, la implementación de scikit-learn del algoritmo KNN se decantará por los vecinos que estén más cerca de la muestra. Si las distancias de los vecinos son similares, el algoritmo elegirá la etiqueta de clase que aparezca primero en el conjunto de datos de entrenamiento.

La elección correcta de k es crucial para encontrar un buen equilibrio entre sobreajuste y subajuste. Además, debemos asegurarnos de que elegimos una métrica de distancia apropiada para las características del conjunto de datos. A menudo, una simple distancia euclidiana se utiliza para muestras de valores reales; por ejemplo, las flores de nuestro conjunto de datos Iris, que tiene características medidas en centímetros. Sin embargo, si estamos utilizando una distancia euclidiana, también es importante normalizar los datos para que cada característica contribuya de forma equitativa en la distancia. La distancia minkowski que hemos utilizado en el código anterior es simplemente una generalización de la distancia euclidiana y de Manhattan, que puede escribirse de la siguiente forma:

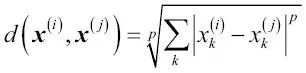
Esto se convierte en la distancia euclidiana si ajustamos el parámetro p=2, o en la distancia de Manhattan en p=1. Scikit-learn dispone de muchas otras métricas de distancia que pueden proporcionarse al parámetro métrico. Estas métricas pueden encontrarse en http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.DistanceMetric.html.

La maldición de la dimensionalidadEs importante mencionar que KNN es muy susceptible al sobreajuste debido a la maldición de la dimensionalidad. La maldición de la dimensionalidad describe el fenómeno donde el espacio de características se vuelve cada vez más escaso para un número cada vez mayor de dimensiones de un conjunto de datos de entrenamiento de tamaño fijo. Intuitivamente, podemos pensar que en un espacio de mayores dimensiones incluso los vecinos más cercanos están demasiado lejos para ofrecer una buena estimación.Ya hemos tratado el concepto de la regularización –en la sección dedicada a la regresión logística– como una manera de evitar el sobreajuste. Sin embargo, en modelos donde la regularización no es aplicable, como en los árboles de decisión podemos usar técnicas de selección de características y reducción de dimensionalidad para ayudarnos a evitar la maldición de la dimensionalidad. Trataremos este aspecto con más detalle en el siguiente capítulo.

Resumen

En este capítulo, has aprendido diferentes algoritmos de aprendizaje automático que se utilizan para abordar problemas lineales y no lineales. Hemos visto que los árboles de decisión son particularmente atractivos si nos preocupamos por la interpretabilidad. La regresión logística no es solo un modelo útil para el aprendizaje online mediante el descenso del gradiente estocástico, sino que también nos permite predecir la probabilidad de un evento en concreto. A pesar de que las máquinas de vectores de soporte sean potentes modelos lineales que se pueden ampliar hasta problemas no lineales mediante el truco de kernel, tienen muchos parámetros que deben ajustarse para poder realizar buenas predicciones. Por el contrario, el conjunto de métodos de los bosques aleatorios no requiere demasiados ajustes de parámetros y no se sobreajusta tan fácilmente como los árboles de decisiones, lo que los convierte en modelos atractivos para distintos dominios de problemas prácticos. El clasificador KNN ofrece un enfoque alternativo a la clasificación a través del aprendizaje vago, que nos permite realizar predicciones sin entrenar ningún modelo pero con un paso de predicción computacionalmente más costoso.