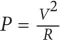Simon Monk - Ejercicios prácticos con Electrónica

Problema

Averiguar cómo se suman los voltajes en un circuito.

Para ello utilizaremos la ley de Kirchhoff del voltaje.

Esta ley establece que la suma total de los voltajes entre diferentes puntos de un circuito es igual a cero.

La Figura 1-6 Figura 1-6. Resistencias en serie . A primera vista no está clara la aplicación de la ley de Kirchhoff del voltaje hasta que reparamos en la polaridad del mismo. A la izquierda, la batería suministra V voltios, que es igual en magnitud, pero de sentido contrario (y por tanto de signo) a los dos voltajes V/2 que atraviesan cada resistencia. Otra manera de verlo es reparar en que el voltaje V debe quedar equilibrado entre los dos voltajes V/2. Es decir: V = V/2 + V/2 o V – (V/2 + V/2) = 0. muestra dos resistencias en serie con una batería. Asumimos que ambas resistencias tienen el mismo valor.

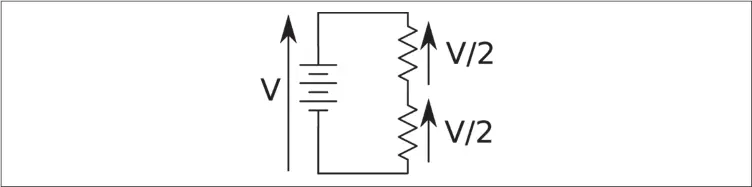
Figura 1-6. Resistencias en serie .

A primera vista no está clara la aplicación de la ley de Kirchhoff del voltaje hasta que reparamos en la polaridad del mismo. A la izquierda, la batería suministra V voltios, que es igual en magnitud, pero de sentido contrario (y por tanto de signo) a los dos voltajes V/2 que atraviesan cada resistencia.

Otra manera de verlo es reparar en que el voltaje V debe quedar equilibrado entre los dos voltajes V/2. Es decir: V = V/2 + V/2 o V – (V/2 + V/2) = 0.

Esta distribución de un par de resistencias se utiliza también para reducir los voltajes (vea el Ejercicio 2.6 2.6 Cómo reducir un voltaje a un valor específico Problema Deseamos reducir un voltaje de CA o CC. ).

Para la ley de Kirchhoff de la corriente, vea el Ejercicio 1.4.

Entender exactamente qué significa potencia en el ámbito de la electrónica.

En electrónica, potencia es la ratio de conversión de energía eléctrica en otro tipo de energía, generalmente calor. Se mide en julios por segundo, magnitud que se conoce por watios (W).

Cuando conectamos una resistencia como en la Figura 1-4 Figura 1-4. Una batería y una resistencia . Gracias a la ley de Ohm sabemos que la corriente es igual al voltaje dividido entre la resistencia del conductor o componente (a efectos prácticos podemos asumir que la resistencia de un cable o hilo conductor es igual a cero). Así que, I = 1,5 / 100 = 0,015 A o 15 mA. del Ejercicio 1.3 1.3 Cómo calcular voltaje, intensidad de la corriente y resistencia Problema Deseamos comprender cómo el voltaje a través de un conductor controla el flujo de corriente a través de aquel. , dicha resistencia disipará la energía eléctrica en forma de calor, y si lo hace de forma significativa, se calentará mucho. Podemos calcular la cantidad de potencia convertida en calor usando la fórmula:

P = I x V

En otras palabras: la potencia en vatios es igual al voltaje que atraviesa la resistencia, en voltios, multiplicado por la intensidad de la corriente en amperios. En el ejemplo que podemos ver en la Figura 1-4 Figura 1-4. Una batería y una resistencia . Gracias a la ley de Ohm sabemos que la corriente es igual al voltaje dividido entre la resistencia del conductor o componente (a efectos prácticos podemos asumir que la resistencia de un cable o hilo conductor es igual a cero). Así que, I = 1,5 / 100 = 0,015 A o 15 mA. , donde el voltaje que atraviesa la resistencia es de 1,5 V y el cálculo de la corriente nos da un valor de 15 mA, el calor disipado es igual a 1,5 V x 15 mA = 22,5 mW.

Si conocemos el voltaje que atraviesa una resistencia y el valor nominal de esta, podemos combinar la ley de Ohm con la expresión P = I x V y utilizar la fórmula:

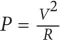
Con V = 1,5 V y R de 100 Ω, la potencia es 1,5 V x 1,5 V / 100 Ω = 22,5 mW.

Para la ley de Ohm, vea el Ejercicio 1.3 1.3 Cómo calcular voltaje, intensidad de la corriente y resistencia Problema Deseamos comprender cómo el voltaje a través de un conductor controla el flujo de corriente a través de aquel. .

Conocer la diferencia entre corriente alterna (CA) y corriente continua (CC).

En todos los ejercicios que hemos visto hasta ahora se da por hecho que tratamos con CC. El voltaje es constante y, por lo general, la alimentación procede de una batería.

La CA es el tipo de corriente que obtenemos de los enchufes de la pared. Este tipo de corriente suele poseer un voltaje alto y peligroso, aunque es posible reducirlo a valores más bajos (vea el Ejercicio 3.9 3.9 Cómo convertir voltajes de corriente alterna (CA) Problema Necesitamos un componente capaz de convertir voltajes de corriente alterna (CA). ). Este voltaje oscila entre 220 y 240 V (en los Estados Unidos, su valor es de 110 V).

La característica alterna de la CA viene del hecho de que el flujo de corriente invierte su sentido múltiples veces por segundo. La Figura 1-7 Figura 1-7. La corriente alterna (CA) . Lo primero en lo que debemos reparar es que el voltaje adopta una forma de onda senoidal, que crece hasta superar los 150 V y, desde allí, disminuye hasta el entorno de -150 V, pasando obviamente por 0 V, y vuelta a empezar. En un ciclo completo, invierte 16,6 milésimas de segundo, aproximadamente (16,6 milisegundos o ms). La relación entre el periodo de CA (tiempo que se tarda en realizar un ciclo completo) y la frecuencia de CA (número de ciclos completos por segundo) es: La unidad de frecuencia es el hercio (Hz). Así, la CA de la Figura 1-7 tiene un periodo de 16,6 ms (0,0166 s) y una frecuencia de: El lector podría estar preguntándose por qué el valor de CA de un enchufe se cifra en 110 V cuando realmente oscila en un rango de más de 300 V. La respuesta es que el valor 110 es el voltaje de CC equivalente que nos proporcionaría la misma potencia. Este valor se denomina voltaje RMS ( Root Mean Square , raíz cuadrada media, o media cuadrática) y es el pico de voltaje dividido entre la raíz cuadrada de 2 (que vale aproximadamente 1,41). Por tanto, en el ejemplo anterior, el pico de voltaje está en 155 V, que dividido entre 1,41 da un resultado de unos 110 V RMS. muestra la variación de voltaje en un enchufe de pared típico (valores para los Estados Unidos).

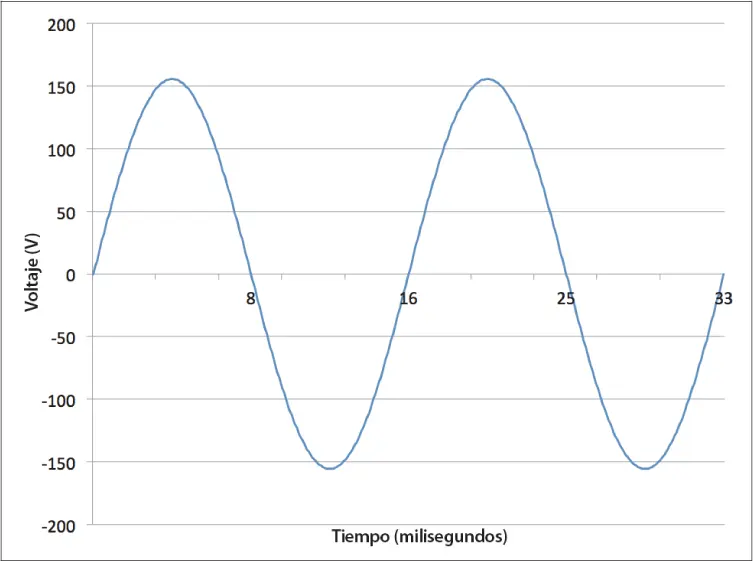
Figura 1-7. La corriente alterna (CA) .

Lo primero en lo que debemos reparar es que el voltaje adopta una forma de onda senoidal, que crece hasta superar los 150 V y, desde allí, disminuye hasta el entorno de -150 V, pasando obviamente por 0 V, y vuelta a empezar. En un ciclo completo, invierte 16,6 milésimas de segundo, aproximadamente (16,6 milisegundos o ms).

La relación entre el periodo de CA (tiempo que se tarda en realizar un ciclo completo) y la frecuencia de CA (número de ciclos completos por segundo) es: