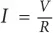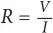Simon Monk - Ejercicios prácticos con Electrónica

Para aprender más sobre voltajes vea el Ejercicio 1.5 1.5 Cómo calcular los voltajes en nuestro circuito Problema Averiguar cómo se suman los voltajes en un circuito. .

Deseamos comprender cómo el voltaje a través de un conductor controla el flujo de corriente a través de aquel.

Utilizaremos la ley de Ohm. La letra griega omega mayúscula (Ω) se utiliza como símbolo para la unidad de medida de la resistencia: el ohmio.

La ley de Ohm indica que el flujo de corriente por un conductor o componente electrónico (I) es igual al voltaje (V) o diferencia de potencial entre los extremos de dicho conductor o componente, dividido entre la resistencia (R) que este ofrece al paso de aquella. En otras palabras:

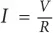
Si deseamos calcular el voltaje, podemos reformular la expresión como:

V = I × R

Por último, si conocemos la corriente, I, que fluye a través de una resistencia, R, con un voltaje V, calcularemos dicha resistencia con la expresión:

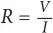
La resistencia es la capacidad que un material tiene de oponerse al paso de la corriente eléctrica. Un conductor debe presentar poca resistencia, porque generalmente no queremos que el flujo de electricidad encuentre dificultades a su paso por aquel. A mayor sección del conductor, menor será la resistencia que presenta para una misma longitud dada. Así pues, un hilo de unas pocas decenas de centímetros que conecte una batería a una bombilla, o más posiblemente a varios LED, en una linterna, tendría una resistencia de entre 0,1 y 1 Ω (ohmio). Mientras que la misma longitud de hilo de mayor sección utilizada, por ejemplo, para conectar un hervidor a un enchufe de CA (corriente alterna) presentaría una resistencia no superior a un par de miliohmios (mΩ).

Resulta muy común el deseo de limitar el flujo de corriente a través de parte de un circuito añadiendo componentes electrónicos llamados resistencias, cuyo efecto es precisamente oponerse al paso de la corriente.

La Figura 1-3 Figura 1-3. Voltaje, intensidad de la corriente y resistencia . Supongamos que vamos a conectar una batería de 1,5 V a una resistencia de 100 Ω como se muestra en la Figura 1-4 . Figura 1-4. Una batería y una resistencia . Gracias a la ley de Ohm sabemos que la corriente es igual al voltaje dividido entre la resistencia del conductor o componente (a efectos prácticos podemos asumir que la resistencia de un cable o hilo conductor es igual a cero). Así que, I = 1,5 / 100 = 0,015 A o 15 mA. muestra una resistencia (línea en zigzag) e indica la corriente (I) que fluye a través de ella así como el voltaje (V).

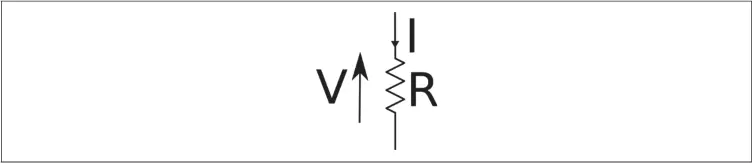
Figura 1-3. Voltaje, intensidad de la corriente y resistencia .

Supongamos que vamos a conectar una batería de 1,5 V a una resistencia de 100 Ω como se muestra en la Figura 1-4 Figura 1-4. Una batería y una resistencia . Gracias a la ley de Ohm sabemos que la corriente es igual al voltaje dividido entre la resistencia del conductor o componente (a efectos prácticos podemos asumir que la resistencia de un cable o hilo conductor es igual a cero). Así que, I = 1,5 / 100 = 0,015 A o 15 mA. .

Figura 1-4. Una batería y una resistencia .

Gracias a la ley de Ohm sabemos que la corriente es igual al voltaje dividido entre la resistencia del conductor o componente (a efectos prácticos podemos asumir que la resistencia de un cable o hilo conductor es igual a cero).

Así que, I = 1,5 / 100 = 0,015 A o 15 mA.

Para entender lo que ocurre con el flujo de corriente a través de resistencias y conductores en un circuito, vea el Ejercicio 1.4 1.4 Cómo calcular la corriente en cualquier punto de un circuito Problema Averiguar el flujo de corriente por cualquier punto dado de un circuito. .

Para entender la relación entre corriente, voltaje y potencia vea el Ejercicio 1.6 1.6 Qué es la potencia eléctrica Problema Entender exactamente qué significa potencia en el ámbito de la electrónica. .

Averiguar el flujo de corriente por cualquier punto dado de un circuito.

Para ello utilizaremos la ley de Kirchhoff de la corriente.

En términos sencillos, la ley de la corriente de Kirchhoff establece que, en cualquier punto de un circuito, el flujo de corriente entrante debe ser igual al flujo de corriente que sale de dicho punto.

Por ejemplo, en la Figura 1-5 Figura 1-5. Resistencias en paralelo . El punto X recibe un flujo de corriente I desde la batería. Sin embargo, de dicho punto salen dos ramas. Si las resistencias tienen el mismo valor, por cada rama fluirá la mitad de la corriente I que llegó al punto X. En el punto Y, las dos rutas se vuelven a unir, así que las dos corrientes I/2 que fluyen a través del punto Y resultarán en la propia corriente I. aparecen dos resistencias en paralelo alimentadas por un voltaje desde una batería (observe el símbolo para la batería a la izquierda de la Figura 1-5 Figura 1-5. Resistencias en paralelo . El punto X recibe un flujo de corriente I desde la batería. Sin embargo, de dicho punto salen dos ramas. Si las resistencias tienen el mismo valor, por cada rama fluirá la mitad de la corriente I que llegó al punto X. En el punto Y, las dos rutas se vuelven a unir, así que las dos corrientes I/2 que fluyen a través del punto Y resultarán en la propia corriente I. ).

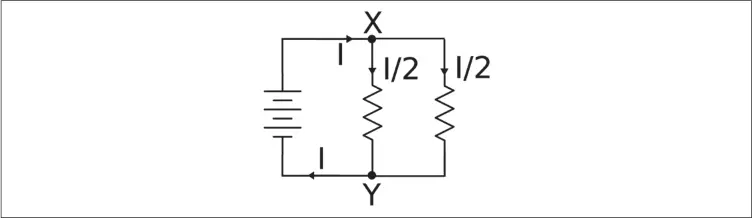
Figura 1-5. Resistencias en paralelo .

El punto X recibe un flujo de corriente I desde la batería. Sin embargo, de dicho punto salen dos ramas. Si las resistencias tienen el mismo valor, por cada rama fluirá la mitad de la corriente I que llegó al punto X.

En el punto Y, las dos rutas se vuelven a unir, así que las dos corrientes I/2 que fluyen a través del punto Y resultarán en la propia corriente I.

Para la ley de Kirchhoff del voltaje, vea el Ejercicio 1.5 1.5 Cómo calcular los voltajes en nuestro circuito Problema Averiguar cómo se suman los voltajes en un circuito. .

Para un análisis más profundo sobre las resistencias en paralelo, vea el Ejercicio 2.5 2.5 Conexión de resistencias en paralelo Problema Comprender la influencia global que tienen las resistencias en paralelo sobre la resistencia y el manejo de la potencia en un circuito. .