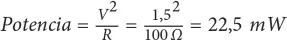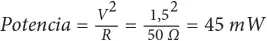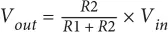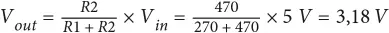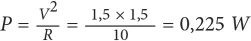Simon Monk - Ejercicios prácticos con Electrónica

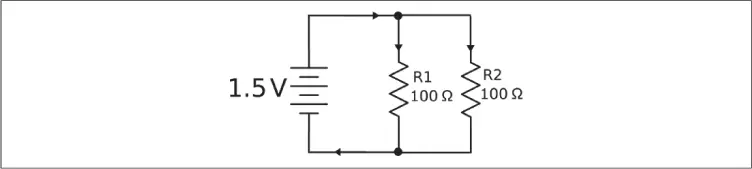
Figura 2-7. Resistencias en paralelo .

En la Figura 2-7, una sola resistencia de 50 Ω equivale a las dos de 100 Ω situadas en paralelo. Ahora bien, ¿cómo influye esto en las potencias nominales de las dos resistencias?

Intuitivamente, lo lógico es suponer que la disipación de potencia total de ambas resistencias de 100 Ω será la misma que en las dos de 50 Ω, pero haremos el cálculo para estar seguros.

Por cada resistencia de 100 Ω, la potencia será:

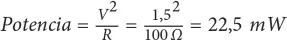
Así que el total de las dos resistencias será de 45 mW, lo que nos permite usar menos potencia y resistencias más comunes.

Como era de esperar, el cálculo para una sola resistencia de 50 Ω nos da:

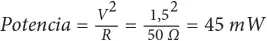
Vea el Ejercicio 2.4para las resistencias en serie.

Deseamos reducir un voltaje de CA o CC.

Utilizar dos resistencias en serie como divisor de voltaje (también llamado divisor de potencial). La palabra potencial indica que la presencia de un voltaje hace posible (potencial) la circulación de la corriente y, por tanto, la realización de trabajo.

La Figura 2-8muestra un par de resistencias usadas como divisor de voltaje.

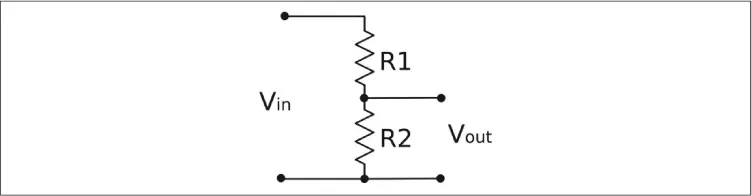
Figura 2-8. Un divisor de voltaje .

El voltaje de salida (Vout) será una fracción del voltaje de entrada (Vin) según la fórmula:

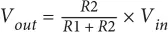
Por ejemplo, si R1 vale 270 Ω; R2, 470 Ω; y Vin, 5 V:

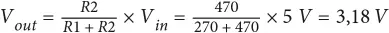
Observe que si R1 y R2 son iguales, el voltaje se divide entre 2.

Un potenciómetro resulta un divisor de potencial que podemos visualizar como dos resistencias, R1 y R2, en serie cuya resistencia total es la misma, pero cuyo valor relativo varía a medida que giramos el pomo. Este es precisamente el funcionamiento de un potenciómetro como control de volumen.

Resulta tentador pensar en un divisor de voltaje como mecanismo útil para reducir este en las fuentes de alimentación. Sin embargo, esto no es así porque, en cuanto tratamos de alimentar algo (enviarle carga eléctrica) a través de la salida del divisor de voltaje, es como si pusiéramos otra resistencia en paralelo a R2. Esto reduce efectivamente la resistencia de la mitad inferior del divisor de voltaje y, por tanto, mengua el voltaje de salida. Esto solo funcionará si las resistencias R1 y R2 son muy inferiores a la resistencia de la carga. Lo que las hace ideales para reducir los niveles de señal, pero no para circuitos de gran potencia.

Vea el Capítulo 7 para aprender diversas técnicas destinadas a reducir voltajes en las fuentes de alimentación. Para los cambios de nivel con un divisor de voltaje, vea el Ejercicio 10.17.

Deseamos conocer la potencia nominal o clasificación de potencia de una resistencia para evitar que se sobrecaliente y falle.

Calcular la potencia (Ejercicio 1.6) que nuestra resistencia disipará en forma de calor y seleccionar una resistencia con una potencia nominal lo bastante superior como para que funcione con seguridad.

Por ejemplo, si tenemos una resistencia de 10 Ω conectada directamente a los terminales de una batería de 1,5 V, la potencia que disipa en forma de calor se puede calcular del siguiente modo:

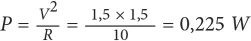
Esto significa que una resistencia estándar de ¼ W resultaría adecuada, pero que podríamos asegurarnos y dar el paso a una de ½ W.

La potencia nominal de las resistencias más usadas por los aficionados es de ¼ W (250 mW). Estas resistencias son lo bastante grandes como para que se puedan manejar cómodamente y sus patillas tienen un grosor suficiente como para hacer buenos contactos con la placa de pruebas ( Ejercicio 20.1). Asimismo, son capaces de manejar cómodamente la potencia requerida en la mayoría de sus usos habituales, como limitar la corriente de los LED ( Ejercicio 14.1) o actuar de divisores de voltaje con corrientes bajas ( Ejercicio 2.6 2.6 Cómo reducir un voltaje a un valor específico Problema Deseamos reducir un voltaje de CA o CC. ).

Otras potencias nominales usuales en resistencias de agujero pasante con patillas son ½, 1, 2, 5 y 10 W, e incluso superiores.

La Figura 2-9muestra una selección de resistencias con diferentes potencias nominales.

En las pequeñas resistencias SMT, o resistencias de chip, que se presentan soldadas en las placas PCB, las potencias nominales empiezan desde mucho más abajo.

Para entender la potencia eléctrica, vea el Ejercicio 1.6.

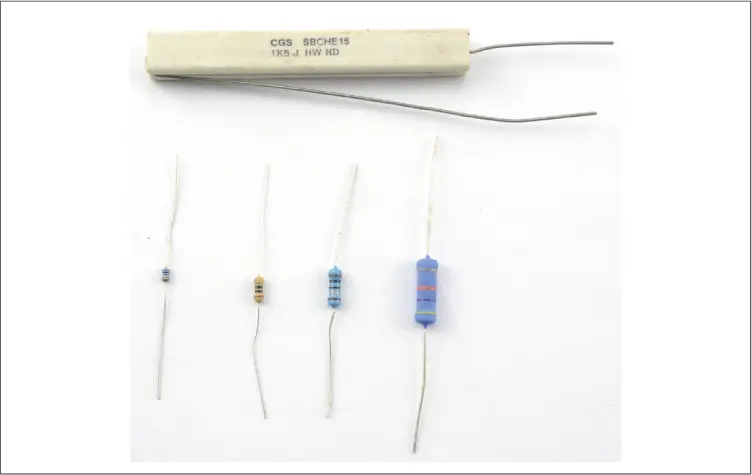
Figura 2-9. Varias resistencias (de izquierda a derecha): 0,125 W, 0,25 W, 0,5 W, 1 W y 7 W (en la parte superior) .

Deseamos realizar la medición de la luminosidad electrónicamente.

Utilizar una fotorresistencia.

Una fotorresistencia ( Figura 2-10) es una resistencia encapsulada en un elemento transparente cuya resistividad varía con relación a la cantidad de luz que recibe. Cuanto mayor sea el brillo que reciba, menor será la resistencia.

Una fotorresistencia típica podría tener una resistividad de 1 kΩ a plena luz del día, que se incrementaría hasta varios MΩ en un ambiente de oscuridad total.

Las fotorresistencias se utilizan a menudo en configuración de divisor de voltaje ( Ejercicio 2.6 2.6 Cómo reducir un voltaje a un valor específico Problema Deseamos reducir un voltaje de CA o CC. ) con una resistencia de valor fijo para convertir la resistividad de la fotorresistencia en un voltaje que podría, luego, usarse en un microcontrolador ( Ejercicio 12.6) o en un comparador ( Ejercicio 17.10).