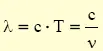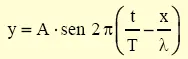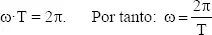Francisco Dalmases Moncayo - Fundamentos físicos de la protección radiológica en odontología

La unidad de frecuencia resulta igual, en consecuencia, a la inversa del segundo, a la que se denomina "hertz" : (ν) SI= s -1= hertz (Hz)

"Longitud de onda" λ: mínima distancia entre dos puntos que se encuentran en idéntico estado de vibración . ( Fig. 2.3 )

Se dice por ello que dos puntos separados una distancia igual a la longitud de onda presentan la misma " fase ", lo que significa mismo estado de vibración de la magnitud vibrante.

Como para cualquier longitud, la unidad de λ en el SI será el metro: (λ) SI= m

Se denomina "frente de ondas" al conjunto de todos los puntos alcanzados a la vez por la onda y que por tanto presentan idéntico estado de vibración, es decir, igual fase.

Figura 2.3 Longitud de onda. Se indica el estado de vibración de los diferentes puntos alcanzados por la onda, así como la envolvente de todos ellos con que habitualmente se representa la onda.

Por consiguiente, una onda presenta realmente una doble periodicidad: temporal y espacial ( Fig. 2.4 ). La onda es periódica en el tiempo, en el sentido de que un punto del espacio alcanzado por la onda experimenta una vibración completa y retorna al estado inicial cada vez que transcurre un intervalo de tiempo igual al periodo T. Y la onda es periódica en el espacio puesto que, en cada instante determinado, dos puntos cualesquiera separados por una distancia λ se encuentran en idéntico estado de vibración. La doble periodicidad puede verificarse en la ecuación de propagación de la onda, tratada en el siguiente subapartado.

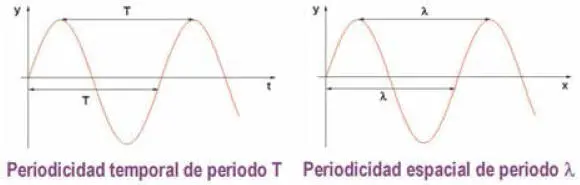
Figura 2.4 Doble periodicidad de una onda.

Ecuación fundamental

Si la velocidad de propagación de la onda en el medio es 'c' , las dos periodicidades temporal T y espacial λ vendrán relacionadas por la ecuación:

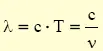
que constituye así la ecuación fundamental de la onda , pese a su sencilla apariencia.

La frecuencia siempre se mantiene constante en una onda, que se limita a reproducir las vibraciones del foco, pero la velocidad de propagación c depende del medio de avance. Por ello la longitud de onda (¡pero nunca la frecuencia!) resulta también dependiente del medio implicado.

Ecuación de propagación

Se habrá definido la ecuación de propagación de una onda cuando, para un punto cualquiera P del espacio, situado a una distancia 'x' del foco ( Fig. 2.5 ), se pueda determinar a través de la ecuación en cuestión cuál es el estado de vibración en P para cualquier instante de tiempo 't'. El estado de vibración quedará caracterizado por el valor instantáneo de la magnitud vibrante con respecto a su valor de equilibrio , que recibe el nombre de "elongación y ". En el caso de que una onda material propague movimientos vibratorios, la elongación 'y' corresponderá a la posición del móvil respecto a la de equilibrio y la onda constituye lo que se denomina un movimiento ondulatorio.

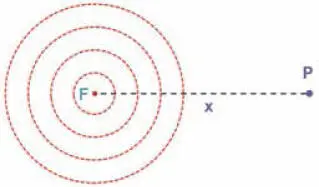
Figura 2.5 Propagación de una onda generada en un foco F.

Si la vibración propagada es de tipo sinusoidal, o "vibración armónica simple", la ecuación de propagación de la onda , por supuesto también sinusoidal, viene dada por:

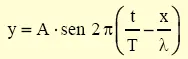
donde y = elongación, T = periodo, λ = longitud de onda, x = distancia al foco, t = tiempo, y A = " amplitud " de la onda, que corresponde al valor absoluto de la máxima elongación que llega a experimentarse.

Como ilustra la Fig. 2.6 , la ecuación permite determinar el estado de vibración de cualquier punto del espacio alcanzado por una onda de amplitud 'A': el situado a una distancia 'a' del foco presentará una elongación 'y a', y el situado a distancia 'b' una elongación 'y b'. Obsérvese que el situado a distancia 'c', como todos los que se encuentran en su mismo semiperiodo, presenta una elongación 'y c' negativa, esto es, inferior al valor de equilibrio, o, si la magnitud vibrante es vectorial, de sentido contrario a su correspondiente valor positivo; en el caso de un movimiento ondulatorio, al otro lado del origen.

Se confirma que la ecuación es doblemente periódica, para 't' con periodo T y para ' x' con periodo λ: al ser el seno una función matemáticamente periódica de periodo 2π, la elongación 'y' retoma el mismo valor cada vez que se incrementa 't' en un número entero de veces T, o 'x' en un número entero de veces λ.

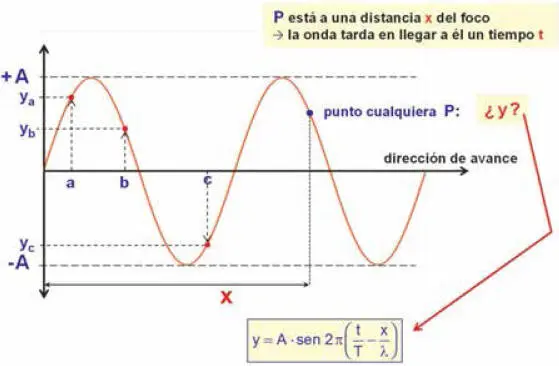
Figura 2.6 Representación gráfica y ecuación de propagación de una onda sinusoidal (ver texto).

La deducción de la ecuación de propagación de una onda (sinusoidal) se proporciona como complemento al final del subapartado.

Las vibraciones del campo eléctrico y el magnético constitutivas de las ondas electromagnéticas son siempre de tipo sinusoidal. En el caso de las ondas materiales también se presentan vibraciones más complejas, pero que siempre es posible descomponer en suma de vibraciones armónicas y simples (teorema de Fourier).

Señalar, por último, que en el contexto general de la propagación de las ondas, éstas pueden ser de dos tipos: " longitudinales ", en las que la dirección de vibración coincide con la de propagación , y " transversales ", en las que la dirección de vibración es perpendicular a la de propagación . Para el caso de las ondas materiales, sólo los sólidos, debido a su elasticidad, permiten los dos tipos de ondas, mientras que en los fluidos sólo pueden existir ondas longitudinales, las cuales propagan compresiones y expansiones en la dirección de avance, como en el caso del sonido. Respecto a los ondas electromagnéticas, son siempre transversales, como se indica en el siguiente apartado 2.4.

Deducción de la ecuación de propagación de una onda sinusoidal

Si la ecuación implícita de vibración del foco en el transcurso del tiempo,

y = f(t), con y = elongación y t = tiempo,

viene dada por una función sinusoidal, que es la de descripción matemática más sencilla (de ahí su denominación de "vibración armónica simple"), la ecuación de vibración del foco será:

y = A 0sen ω t

con A 0y ω dos constantes:

- A 0es, obviamente, la amplitud en el foco, puesto que el valor máximo de la función seno es 1, y

- ω debe responder a que el periodo matemático de la función seno es 2π; por lo que al multiplicar ω por un tiempo 't' igual al período T de la vibración, debe devolver el valor 2π:

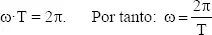
Se le denomina " frecuencia angular " o " pulsación ".