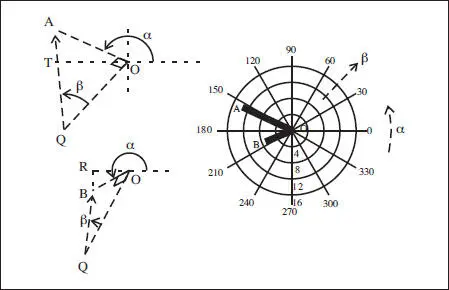
Fig. 2.14 Esquemas de obtención de los parámetros (α,β) de Listing y representación gráfica de los dos movimientos terciarios del problema 1.
b ) El ángulo de falsa torsión ω asociado a cada uno de los dos movimientos oblicuos son:
– Para el movimiento O→A:
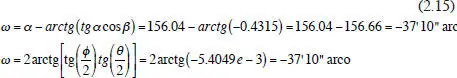
– Para el movimiento O→B:
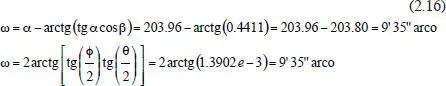
Problemas propuestos
2. Supongamos a tres estudiantes situados a una distancia de 10 m en línea recta respecto del borde inferior de la pizarra, que mide 4 m de ancho por 1.8 m de alto. Dos de ellos O 1y O 2se sitúan en posición primaria respectivamente con relatión a los bordes inferior-izquierdo e inferiorderecho de la pizarra; mientras que el tercero O 3se encuentra en posición primaria en la mitad inferior de la pizarra. Averigua cuál es la falsa torsión co asociada a los movimientos oculares de los tres estudiantes cuando pasan de su respectiva posición primaria al centro de la pizarra C. ¿Es cierto que ω 1= ω 2? Justifica la respuesta.
Solución: para el movimiento ocular 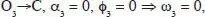 , el movimiento ocular es una elevatión o latitud
, el movimiento ocular es una elevatión o latitud 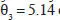 deg ; en los movimientos oculares
deg ; en los movimientos oculares 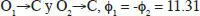 deg,
deg, 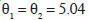 deg, por lo que
deg, por lo que 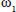
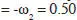 deg.
deg.
3. Una persona realiza un movimiento ocular terciario O→C con una falsa torsión asociada ω = -3.24 deg. Los parámetros de Helmholtz de este movimiento ocular son  deg. Calcula:
deg. Calcula:
a ) Los parámetros de Fick (ϕ, θ) de este movimiento ocular.
b ) Los parámetros de Listing (α,β) de este movimiento ocular.
c ) Si el punto de observatión primaria O se encuentra a 400 m del sujeto, ¿cuál es la distancia real entre los puntos O y C?
Solución : 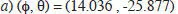 deg;
deg; 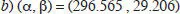 deg ;
deg ;  .
.
3. Dinámica del ojo
3.1 Consideraciones geométricas previas
Considerado pues el ojo como una esfera libre en el espacio tridimensional, veamos cuáles son los mecanismos que permiten moverla libremente. En general, si queremos mover una esfera cualquiera en las tres direcciones del espacio XYZ, es necesario desarrollar al menos 6 fuerzas que generen tres pares de éstas. Con este preámbulo, y teniendo en cuenta la posición de la córnea y la dirección de entrada de la luz (dirección sagital X), tenemos lo siguiente ( fig. 3.1):

Fig. 3.1 Pares de fuerzas para girar libremente una esfera en el espacio tridimensional.
– Para permitir una rotación alrededor del eje Y (abducción y adducción), y que no estorbe el paso de la luz, hacen falta un par de fuerzas sobre el eje Z.
– Para permitir una rotación alrededor del eje Z (elevación y descenso), y que no estorbe el paso de la luz, hacen falta un par de fuerzas sobre el eje Y.
– Para permitir una rotación alrededor del eje X (extorsión e intorsión), hacen falta un par de fuerzas alrededor de la sección circular de la esfera en el plano de Listing que no interfieran en las posiciones de los dos anteriores pares de fuerzas.
En el sistema anatómico del ojo, la naturaleza ha desarrollado exactamente seis músculos que permiten los tres pares de fuerzas comentados. Teniendo en cuenta varias secciones anatómicas del globo ocular ( fig. 3.2), vemos que los músculos recto externo (RE) e interno (R Int.) son los que permiten los giros alrededor del eje Y (abducción y adducción); los músculos recto superior (RS) e inferior (R Inf.) son los responsables de poder girar alrededor del eje Z (elevación y descenso); y los músculos oblicuos superior (OS) e inferior (OI), con sus particularísimos sistemas de inserción ocular, se centran en los giros alrededor del eje X (extorsión e intorsión).
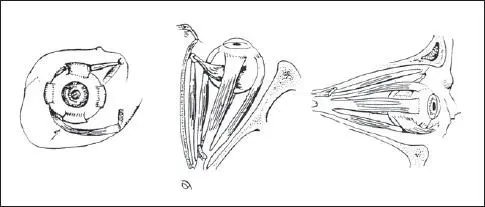
Fig. 3.2 Secciones anatómicas de la órbita ocular derecha para mostrar los músculos extraoculares. Izquierda: vista frontal; centro: vista superior; derecha: vista lateral.
No obstante, como veremos a continuación, las acciones de estos músculos no son tan sencillas como así parecen a partir de este razonamiento puramente geométrico.
3.2 Teoría clásica vs. moderna de las acciones músculo-oculares
El modelo clásico de rotaciones oculares se debe a Duane (1896, 1919, 1934), aunque ha sido extendido por los resultados de Boeder y Jampel (Tunnacliffe, 1997). En principio, el modelo clásico explica correctamente las acciones músculo-oculares a partir de la posición primaria de mirada (ejes visuales paralelos), pero falla cuando el movimiento ocular no empieza desde la posición primaria, que es justamente lo que complementan los resultados de la teoría moderna.
Para entender con profundidad las acciones músculo-oculares es necesario, en primer lugar, definir una serie de conceptos sencillos ligados a un esquema geométrico ( fig. 3.3) donde se ilustra un músculo extraocular como una cuerda unida al globo ocular:
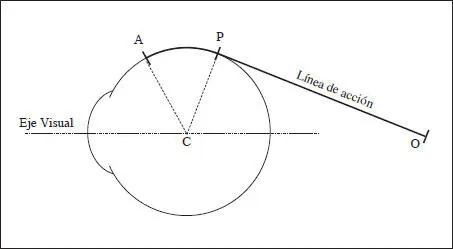
Fig. 3.3 Inserciones de los músculos extraoculares en el globo ocular.
Inserción ocular o anatómica (A): es el punto de inserción fija de los músculos en el globo ocular.
Inserción orbitaria (O): es el punto de la órbita del ojo donde se inserta el músculo.
Inserción fisiológica (P): punto tangente donde se aplica la fuerza del músculo al globo ocular.
Читать дальше


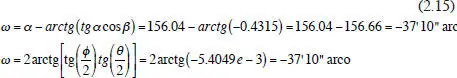
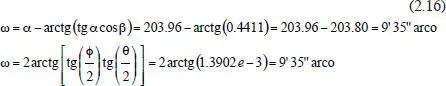
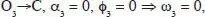 , el movimiento ocular es una elevatión o latitud
, el movimiento ocular es una elevatión o latitud 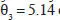 deg ; en los movimientos oculares
deg ; en los movimientos oculares 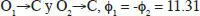 deg,
deg, 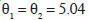 deg, por lo que
deg, por lo que 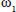
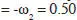 deg.
deg. deg. Calcula:
deg. Calcula: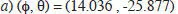 deg;
deg; 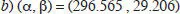 deg ;
deg ;  .
.













