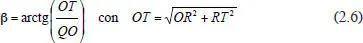Posición secundaria: aquella a la que se llega a través de un movimiento secundario de giro alrededor de los ejes Y o Z.
Posición terciaria: cualquier otra posición a la que se llega girando alrededor de un eje que no sea de Fick.
Las rotaciones monoculares que puede realizar el ojo se denominan ducciones y se pueden clasificar en:
Supraducción: elevación alrededor del eje Z.
Infraducción: depresión o descenso alrededor del eje Z.
Abducción: giro hacia el lado temporal alrededor del eje Y. También se denomina dextroducción en el OD y levoducción en el OI.
Adducción: giro hacia el lado nasal alrededor del eje Y. También se denomina levoducción en el OD y dextroducción en el OI.
Intorsión o inciclotorsión: giro alrededor del eje X en dirección nasal.
Extorsión o exciclotorsión: giro alrededor del eje X en dirección temporal.
Los movimientos terciarios se pueden descomponer en dos movimientos secundarios y su notación es la composición de los dos nombres. Así, un movimiento del ojo hacia el lado nasal y hacia arriba del ojo derecho se denominaría levosupraducción ( fig. 2.4).
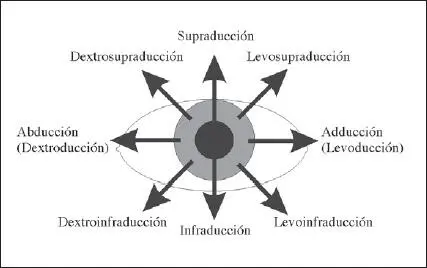
Fig. 2.4 Ducciones en el ojo derecho.
2.5 Sistemas de representación de los movimientos oculares
A la hora de plantear la cuestión de qué camino elige el ojo cuando realiza un movimiento oblicuo –desde la posición primaria O a la posición terciaria T– tenemos de partida que éste puede elegir voluntariamente infinitos caminos o rutas, pero lo que nos interesa es averiguar la ruta que elige involuntariamente. Desde un punto de vista lógico, el ojo elige siempre involuntariamente la ruta más corta, la del mínimo esfuerzo, la que podemos trazar visualmente a lo largo del segmento OT que une los dos puntos, pero ¿qué tipo de rotaciones monoculares implica hacer esto?, ¿se puede ejecutar este movimiento con un único giro, o es necesario hacer más de uno?
Para contestar a estas preguntas vamos a presentar varias rutas o caminos, las cuales nos conducirán a comprender las leyes de Donders y de Listing de los movimientos oculares, que presentaremos en el apartado siguiente. Para ello desarrollaremos un ejemplo numérico asociado a un esquema característico ( fig. 2.5) en el que las posiciones primaria O y la terciaria T forman un rectángulo cuyos dos vértices adicionales son los puntos S (encima de O y a la izquierda de T) y R (a la derecha de O y debajo de T), todos ellos en un plano perpendicular al eje de fijación.
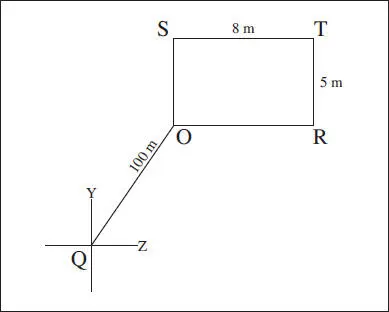
Fig.2.5 Ejemplo numérico de un movimiento terciario u oblicuo O→T
2.5.1 Ruta de Helmholtz
Propuesta por uno de los grandes científicos del siglo XIX, y «padre» de la Óptica Fisiológica, esta ruta plantea dos movimientos oculares ( fig. 2.6):
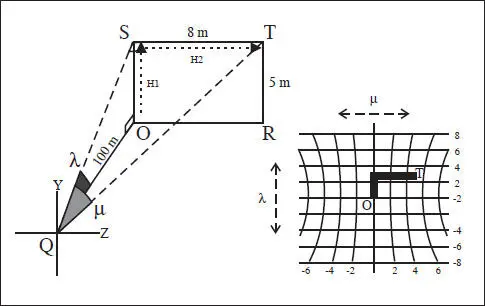
Fig. 2.6 Ruta de Helmholtz y sistema asociado de representación (Φ,μ) de los movimientos oculares.
– Sub-ruta H1: elevación (o descenso) λ, de O a S:

– Sub-ruta H2: giro fuera del plano de Listing denotado como azimuth μ, de S a T:
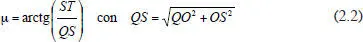
Simplemente, plantea la ruta que saldría a través de la esquina superior-izquierda del rectángulo de vértices OSTR. Para el ejemplo numérico, obtenemos λ = +2.86 deg y μ = +4.57 deg.
Con estos dos parámetros de giro se puede formar un sistema no cartesiano de representatión dado que el azimuth no es un movimiento secundario, donde la variable horizontal es A. y la vertical μ ( fig. 2.6, derecha), y en el que el origen es O y la positión final o terciaria es 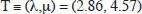 deg para el ejemplo desarrollado.
deg para el ejemplo desarrollado.
2.5.2 Ruta de Fick
Al igual que la anterior, se proponen dos sub-movimientos oculares ( fig. 2.7):
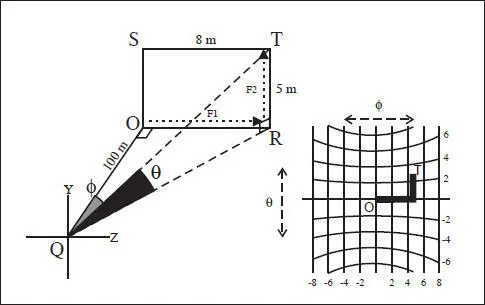
Fig. 2.7 Ruta de Fick y sistema asociado de representación (ϕ,θ) de los movimientos oculares.
– Sub-ruta F1: longitud ϕ, de O a R:

– Sub-ruta F2: giro fuera del plano de Listing denotado como latitud θ, de R a T:
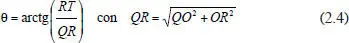
Simplemente, plantea la ruta que saldría a través de la esquina inferiorderecha del rectángulo de vértices OSTR. Para el ejemplo numérico, obtenemos (ϕ)= +4.57 deg y θ = +2.85 deg.
Con estos dos parámetros de giro se puede formar otra vez un sistema no cartesiano de representatión dado que la latitud no es un movimiento secundario, donde la variable horizontal es ϕ y la vertical θ ( fig. 2.7, derecha), y en el que el origen es O y la positión final o terciaria es 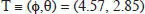 deg para el ejemplo desarrollado.
deg para el ejemplo desarrollado.
2.5.3 Ruta de Listing
Se basa en que el ojo va a ejecutar el camino más corto entre O y T, es decir, a través de la diagonal del rectángulo de vértices OSTR ( fig. 2.8). Para ello, el ojo parece conocer el ángulo relativo α entre O y T, el cual se denota como meridiano y se deduce a partir de:

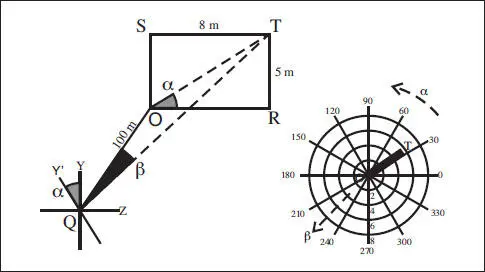
Fig. 2.8 Ruta de Listing y sistema asociado de representatión (ϕθ) de los movimientos oculares.
Tenido en cuenta el ángulo α, Listing encontró que, girando el eje Y de Fick un valor α, el ojo puede girar directamente de O a T con un valor β, denotado como excentricidad y que se deduce a partir de:
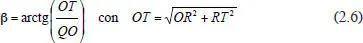
En principio, la única rotación monocular que se haría sería el valor β y no el valor α, puesto que lo asociamos a un giro de los ejes de Fick y no del ojo. Aun así, no podríamos identificar la rotación β como un tipo de ducción. Consecuentemente, el sistema de representación asociado a esta ruta es exclusivamente polar o curvilíneo, nunca cartesiano (fig. 2.8, derecha). Para el ejemplo numérico desarrollado, se obtiene que α = 32.01 deg y β = 5.39 deg, que serán por tanto las coordenadas polares asociadas a la posición terciaria T.
Читать дальше





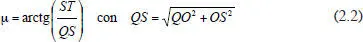
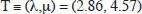 deg para el ejemplo desarrollado.
deg para el ejemplo desarrollado.

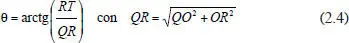
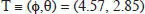 deg para el ejemplo desarrollado.
deg para el ejemplo desarrollado.