Francisco M. Martínez Verdú - Fundamentos de visión binocular

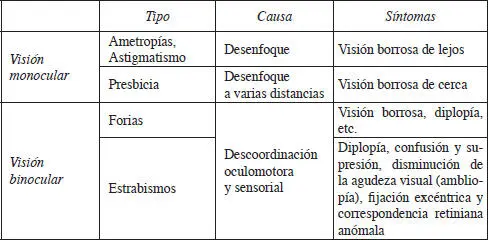
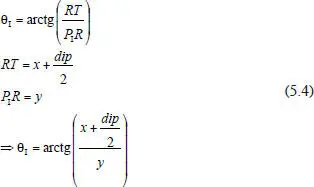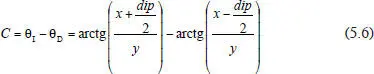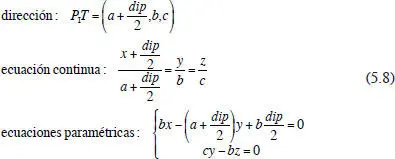Como guía inicial, creemos que vale la pena repasar los problemas visuales típicos relacionados con la visión monocular; en concreto, el origen y los síntomas de las ametropías esféricas (miopía e hipermetropía), el astigmatismo y la presbicia. Todos ellos provocan una visión borrosa: las ametropías y el astigmatismo para visión lejana, la presbicia para visión cercana. Las ametropías y el astigmatismo se deben principalmente a un desequilibrio entre la potencia de los componentes dióptricos (córnea y cristalino) del ojo y su longitud axial. En cambio, la presbicia aparece debido a una disminución temporal y gradual de la capacidad del cristalino para aumentar su potencia para reducir el desenfoque a varias distancias. Por lo tanto, el síntoma óptico clave de estos problemas visuales es el desenfoque óptico cerca de la retina o error refractivo (Rabbetts, 1998; Romero, et al., 1996; Tunnacliffe, 1997;Viqueira, Martínez-Verdú, de Fez, 2004), y su repercusión sensorial principal es la visión borrosa.

Respecto a las anomalías binoculares, una vez llegados a este capítulo, ya somos conscientes de la variedad de causas posibles de las forias y los estrabismos. Por tanto, para finalizar este capítulo, solamente nos resta avanzar los síntomas visuales típicos de estas anomalías visuales para tener constancia de la complejidad con que se enfrenta la optometría binocular, un esfuerzo de análisis y comprensión que pretendemos aligerar o complementar con esta monografía siguiendo una estrategia que ya han establecidos otros (Reading, 1983; Regan, 1991; Steinman, Steinman, Garzia, 2000).

TABLA 5.5

Síntomas óptico-sensoriales de las anomalías monoculares y binoculares.

PROBLEMAS

Problemas resueltos

1. Consideremos el cálculo trigonométrico de la convergencia asimétrica 2D en el plano de fijación tal como se muestra en el esquema adjunto ( fig. 5.12). Sea T( x , y ) el test puntual sobre el que deseamos dirigir la mirada desde la posición primaria, S(0,0) nuestro origen de referencia, situado en el punto medio de la distancia interpupilar (P IP D= dip), y los puntos P I(-dip/2,0) y P D(dip/2,0) las posiciones pupilares de nuestros ojos. Se pide:

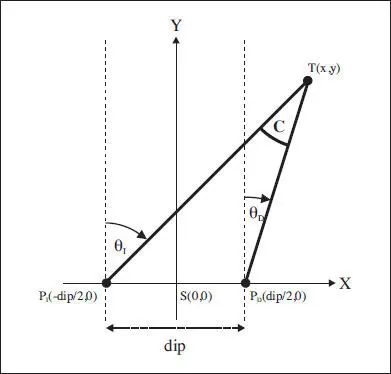
Fig. 5.12 Esquema inicial del problema resuelto n° 1 acerca del cálculo de la convergencia asimétrica (2D) en el plano de fijación.

a) Las expresiones generales de las rotaciones monoculares θ Iy θ D, así como la del ángulo de convergencia C.

b) Aplica las expresiones anteriores al ejemplo numérico de T(25,50 cm) y dip = 64 mm.

a) El esquema initial ( fig. 5.13) muestra que el estímulo puntual se encuentra a la derecha del ojo derecho, por lo que las rotaciones monoculares son adductión (θ I) en el ojo izquierdo y abductión (θ D) en el ojo derecho. Teniendo en cuenta las indicaciones de la Tabla 5.1, conocemos que siendo θ I> θ Dnos queda que la convergencia es:

Desde un punto de vista trigonométrico, el cálculo de las rotaciones monoculares y la convergencia se apoya en los puntos imaginarios complementarios R(-dip/2, y > y Q(dip/2, y ) de la fig. 5.13.

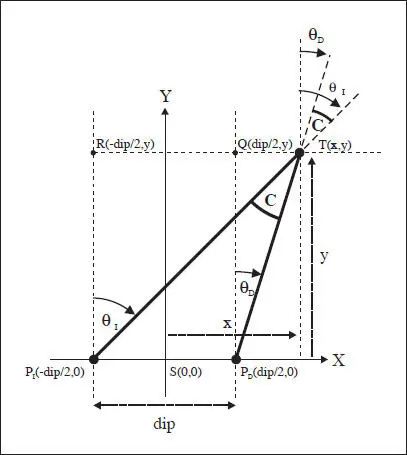
Fig. 5.13 Esquema completo del problema resuelto n° 1.

Apoyándonos en el triángulo rectángulo P rRT, tenemos que la adducción θ Ise expresa como sigue:

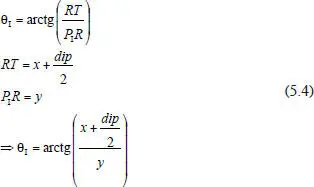
De modo similar, apoyándonos ahora en el punto complementario Q, el cálculo trigonométrico de la abducción θ Des el siguiente:

Por tanto, la convergencia asimétrica C en el plano de fijación para un estímulo situado al lado derecho del campo visual binocular es:

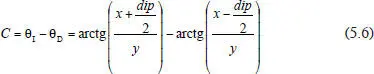
b ) Con las expresiones anteriores, pasamos ahora a resolver un ejemplo numérico. Para este caso, el estímulo T se encuentra 25 cm a la derecha del centro de referencia (en medio de los dos ojos) y 50 cm por delante de los ojos. Tomando la distancia interpupilar dip = 6.4 cm, tenemos que:

2. Sea el problema geométrico del cálculo de la convergencia asimétrica en el espacio puntual 3D ( fig. 5.13), donde los ojos están en las posiciones P I(-dip/2,0,0) y P D(dip/2,0,0) y están mirando hacia un objeto puntual T(a,b,c). Se pide:

a) Las ecuaciones de las rectas que marcan los ejes visuales izquierdo y derecho.

b) La expresión general del ángulo de convergencia como intersectión de los dos ejes visuales en el punto T(a,b,c). Aplica la expresión obtenida a los ejemplos numéricos siguientes: dip = 64 mm, T 1(25,50,0) cm y L.(25,50,-50) cm.

c) Las rotaciones monoculares a partir de sus respectivas posiciones primarias de reposo. Aplica otra vez las expresiones obtenidas a los ejemplos numéricos siguientes: dip = 64 mm, T 1(25,50,0) cm y T 2(25,50,-50) cm.

a) El cálculo de la convergencia asimétrica 3D parte de un planteamiento geométrico completamente diferente del anterior, pero que servirá para establecer diferencias y similitudes. El esquema initial ( fig. 5.14) sirve para percibir que la resolutión completa del problema será mucho más compleja que la anterior. Para empezar, las rotaciones monoculares no son directamente ducciones, sino movimientos terciarios, por lo que tendrán asociadas falsas torsiones (capítulo 2).

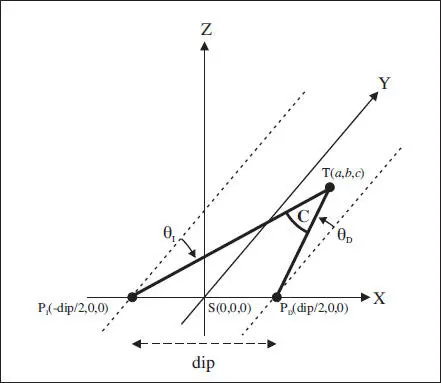
Fig. 5.14 Esquema inicial del problema resuelto n° 2 acerca del cálculo de la convergencia asimétrica 3D (fuera del plano de fijación).

Para centrarnos, el primer apartado plantea la obtención de las expresiones para las rectas que marcan los ejes visuales izquierdo y derecho. Conocidos dos puntos de una recta, podemos obtener su dirección (vector director) y las ecuaciones continua y paramétricas (dos ecuaciones al ser en el espacio tridi-mensional).

Para el eje visual izquierdo EV I, el vector director es P IT, con lo que obtenemos:

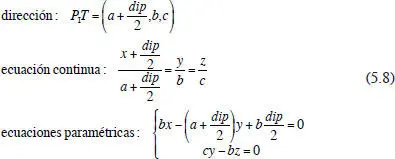
Para el eje visual derecho se obtiene procediendo de modo similar: