Francisco M. Martínez Verdú - Fundamentos de visión binocular

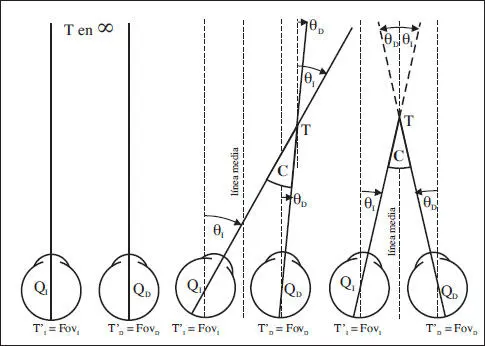
Fig. 5.5Casos de convergencia en el plano de fijación. Izquierda: convergencia nula asociada a la posición primaria (objeto muy lejano). Centro: convergencia asimétrica (2D). Derecha: convergencia simétrica (total).

Otro aspecto que cabe aclarar en estos momentos es qué convenio de signos debemos utilizar con las vergencias. Esto también tiene que ver con cuánto gira monocularmente cada ojo cuando se realiza una vergencia. De partida tenemos el criterio horario: los giros antihorarios son positivos, y los giros horarios negativos. Aplicando este criterio al caso particular de los ojos, tanto para el ojo derecho como para el ojo izquierdo (la línea media simularía un espejo), tenemos que las rotaciones monoculares hacia el lado nasal (superior) son positivas, y hacia el lado temporal (inferior) son negativas. Con estas consideraciones, podemos deducir fácilmente de la última figura las contribuciones de las rotaciones monoculares para la convergencia asimétrica 2D y la convergencia simétrica. La fórmula general es directamente la suma de las rotaciones monoculares:

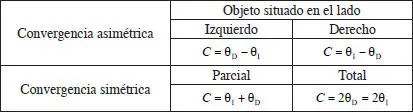
pero, el valor final, incluido su signo, depende de la posición del objeto respecto de los dos ojos. En convergencia asimétrica 2D (y 3D) poco importa el signo, pero el resultado final siempre será la diferencia entre las rotaciones monoculares ( fig. 5.5, centro). En cambio, en convergencia simétrica, total o parcial (cuando el objeto queda entre los dos ojos pero no justamente en la línea media), el resultado final es siempre la suma de las dos rotaciones monoculares. Si es convergencia simétrica total, será justamente el doble de la rotación monocular ( fig. 5.5, derecha), siendo positiva cuando los ojos convergen porque el objeto es real, o negativa, cuando los ojos divergen porque el objeto es virtual. Para aclarar quizás al lector, proponemos la tabla siguiente en la que enumeramos los casos citados obviando el signo de las rotaciones monoculares:

TABLA 1

Casos de convergencia en el plano de fijación.

5.2.3 Componentes de la vergencia

Las vergencias son movimientos muy complejos, ya que están relacionados tanto con la acomodación como con el mecanismo fusional. Si la borrosidad del objeto es el principal estímulo de la acomodación, la disociación de las dos imágenes retinianas o disparidad retiniana, que puede generar diplopía, puede asumirse a priori como el principal estímulo de la vergencia. Sin embargo, fue Maddox en 1893 quien identificó cuatro tipos de componentes en la respuesta vergencial: fusional, acomodativa, tónica y proximal. Es decir, que el ángulo de vergencia C puede descomponerse en cuatro ángulos menores, cuyo peso o importancia relativa no se analizarán hasta el tema siguiente. Esta clasificación se mantiene hasta la fecha con ciertos detalles que vamos a presentar a continuación.

Vergencia fusional

Es la componente de la vergencia inducida por la disparidad objeto (retiniana), es decir, cuando un objeto llega a verse doble. Al desplazarse un objeto, deja de verse fusionado (de forma haplópica) y la diplopía actúa como estímulo para la vergencia, que se producirá en la dirección adecuada para favorecer la haplopía. Parece ser que es independiente del color de los objetos y que está relacionada con la información de formas grandes, es decir, con las características del sistema magnocelular.

La disparidad objeto es la variación de la posición horizontal relativa de los objetos de una escena sin cambiar el tamaño, ni la forma, ni la distancia de visualización. Como se puede observar en la fig. 5.6, cada par de círculos concéntricos, situado en cada ojo a la misma distancia, presenta un pequeño desplazamiento (la disparidad objeto) que generará una diferencia en las posiciones angulares de sus respectivas imágenes retinianas, que se denota habitualmente como disparidad retiniana o binocular. Por tanto, para no verlo doble, los ojos vergerán adecuadamente y conseguirán de forma simultánea una sensación de profundidad relativa (estereopsis) entre ambos círculos. Como se demostrará mucho más tarde (capítulo 13), la disparidad retiniana η para este caso particular de estereograma se relaciona directamente con la disparidad objeto o desplazamiento lateral Δπ entre los objetos y la distancia de observación d :

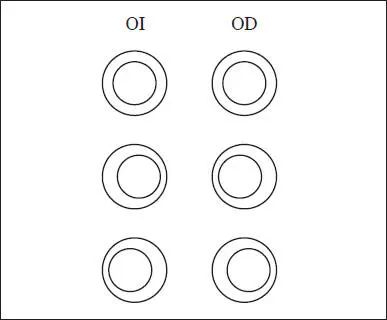
Fig. 5.6 Parejas estereoscópicas típicas para analizar la vergencia fusional con un sinoptóforo presentando cada parte en cada ojo (aunque puede conseguirse la misma sensación estereoscópica aplicando las técnicas de fusión libre que se explicarán en el capítulo 13). Arriba: los círculos son concéntricos por lo que no existe disparidad retiniana. Centro: los círculos pequeños se han desplazado 2 mm hacia dentro, lo que genera una disparidad convergente de 0.01 rad (0.573 deg) a 50 cm. Abajo: los círculos pequeños se han desplazado 2 mm hacia fuera, lo que genera una disparidad divergente de 0.01 rad (0.573 deg) a 50 cm.

Con este tipo de estereogramas y manteniendo la distancia de fijación, podríamos reproducir los resultados clásicos de Rashbass y Westheimer (1961) acerca de la características dinámicas de la vergencia fusional (Judge, 1991). Con las demás componentes vergenciales constantes, la velocidad de vergencia fusional v , ya sea convergente o divergente, es directamente proporcional a la disparidad objeto Δπ, y por ende, a la disparidad retiniana η. En concreto, el experimento ya clásico demostró que la velocidad de vergencia fusional era de 5–10 deg/s por cada grado de disparidad retiniana. Otros detalles interesantes de este experimento, complementados más adelante por otros investigadores, son que el tiempo de reacción típico de la vergencia fusional es de 160 ms, que el tamaño mínimo de disparidad retiniana para iniciar la vergencia debe ser inferior a 6ʼ (menos de 0.44 mm de disparidad objeto para el estereograma de la fig. 5.6visto a 50 cm), y que para disparidades retinianas superiores a 4 deg (más de 17.45 mm de disparidad objeto) la velocidad de vergencia fusional decae progresivamente con el tamaño de la disparidad ante la imposibilidad de fusionar perceptualmente.

Vergencia acomodativa

La vergencia también se produce al cambiar la acomodación. Un buen ejemplo es la experiencia de Müller (1826), en la que un observador debe fijar un objeto móvil sobre el eje visual del ojo derecho mientras el ojo izquierdo está ocluido, tal y como se muestra en la fig. 5.7. Al variar la ubicación del objeto de la posición A a la B, el ojo derecho tan solo cambia su acomodación, y el OI no tiene ningún estímulo visual, por lo que no debería cambiar su situación. Sin embargo, cuando se cambia la posición del objeto, se comprueba que existe un movimiento en el ojo ocluido que coincide con el del objeto: de convergencia si se acerca y de divergencia si se aleja. El mismo efecto puede apreciarse si, fijando la posición del test, colocamos una lente divergente ante el ojo descubierto. En tales circunstancias, éste deberá sobreacomodarse para compensar la borrosidad que le provoca la lente divergente, con lo que el valor de convergencia que ejerce el ojo ocluido será proporcional al valor de la potencia de la lente. El valor típico de la vergencia acomodativa es de 0.8-0.9 A am, siendo A la acomodación en dioptrías [D].