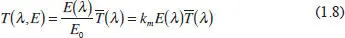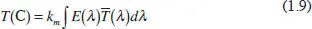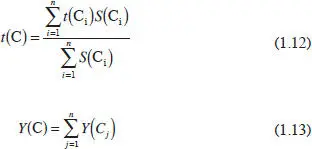Por otra parte, si lo que cambia es la luz que ilumina la escena de la que forma parte el objeto, los valores triestímulo del mismo, desde luego, cambiarán, pero el color percibido no cambia de acuerdo con la predicción que se realizaría del cambio de los valores triestímulo, debido a que el sistema visual es capaz de descontar parcialmente el iluminante de la luz que le llega al ojo, reduciendo de manera dinámica los cambios de color que se producen permanentemente en los objetos. Este comportamiento del sistema visual es lo que se conoce como constancia del color . Para que el sistema visual pueda descontar el color del iluminante, es condición necesaria que la reflectancia promedio espacial de la escena sea neutra, ya que sólo si esto ocurre, el color promedio espacial de la escena, que de alguna manera el sistema visual puede computar y eliminar, será precisamente el color del iluminante. La capacidad para separar la reflectancia y el iluminante a partir de la información de la luz que se recibe de la escena es, por supuesto, una propiedad extraordinaria del sistema visual, ya que si no fuera así, difícilmente el color resultaría útil para la identificación de los objetos. Debe quedar claro que, con un color aislado, no se dan las condiciones necesarias para que el sistema visual pueda realizar esta tarea y, por consiguiente, no habrá en absoluto constancia del color.
¿Quiere decir todo lo expuesto hasta aquí que la colorimetría triestímulo es algo de lo que ya debemos olvidarnos? Naturalmente, la respuesta es no. El cálculo de los descriptores perceptuales del color mediante cualquier modelo de apariencia comienza siempre con los valores triestímulo en un espacio estándar, generalmente el espacio CIE-XYZ, seguido de un cambio a un espacio de excitación de conos (espacios LMS), donde arranca el proceso visual que conduce a la percepción del color. Por otro lado, buena parte de las aplicaciones prácticas del color, como algunas de las descritas en este libro, utilizan básicamente colorimetría triestímulo, por lo que su conocimiento es, sin duda, fundamental. No obstante dar por sentado que el lector de este libro conoce sobradamente la colorimetría triestímulo, este capítulo pretende ser un manual práctico que pueda usarse en cualquier momento durante el estudio de cualquiera de los capítulos que lo componen, incluyendo además un resumen de la misma, las fórmulas y datos adicionales más usuales en la tecnología del color, tales como, por ejemplo, los espacios CIELAB y CIELUV y la fórmula de diferencia de color CIE94. Por otra parte, se pretende familiarizar al lector con la nomenclatura que se utlizará en el resto del libro.
1.2 Definición de espacio de representación del color. Vector triestímulo y coordenadas cromáticas
Sean los primarios P 1, P 2, P 3. Sea el blanco de referencia W con luminancia Y(W) y sean Y W(P 1), Y W(P 2), Y W(P 3) las luminancias de los primarios que igualan el blanco (unidades tricromáticas). Se definen los valores triestímulo del color C, de la forma:
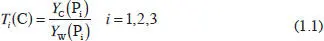
La relación entre los valores triestímulo y la luminancia se puede escribir:
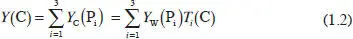
Se definen las coordenadas cromáticas de C de la forma:
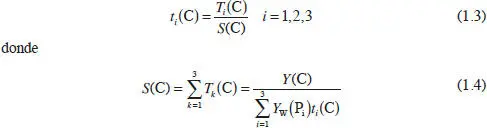
Nótese que, por definición, las coordenadas cromáticas de un color son independientes de la luminancia del mismo. Además, las coordenadas de un color cualquiera suman la unidad y, por consiguiente, sólo dos de ellas son linealmente independientes. Así pues, para tener la misma información sobre el color que se tenía con los valores triestímulo, será necesario dar una pareja de coordenadas, por ejemplo (t 1(C), t 2(C)), y la luminancia Y(C).
Por último, la relación entre los valores triestímulo, las coordenadas cromáticas y la luminancia resulta:
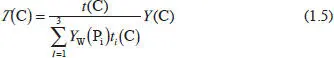
A una representación bidimensional del color (generalmente t 1(C) en abcisas, t 2(C) en ordenadas) se le denomina diagrama cromático . Si se representan las coordenadas cromáticas de los colores espectrales y se traza la curva que los une, se obtiene el denominado locus espectral . La recta que une los extremos de dicho locus se conoce como recta de los púrpuras . El espacio interior limitado por el locus espectral y la recta de los púrpuras contiene todos los colores reales.
1.3 Definición de funciones de igualación de color
Las funciones de igualación de color son los valores triestímulo de los colores espectrales con energía E 0= 1/k m, (k m=683), o lo que es lo mismo, con luminancia Y 0(λ) = V(λ), donde V(λ) es el observador patrón CIE (1924); (apéndice III). Por consiguiente:
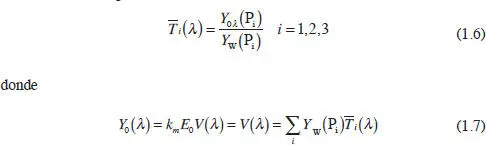 1.4 Cálculo de valores triestímulo a partir de las funciones de igualación
1.4 Cálculo de valores triestímulo a partir de las funciones de igualación
Para un color espectral, λ, de energía E(λ):
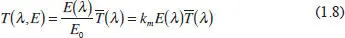
Para un color de espectro continuo:
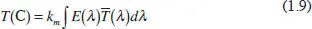
1.5 Cálculo de mezclas de colores
Sean los colores C j. De la linealidad de los valores triestímulo, el vector triestímulo de la mezcla será:

o en términos de las luminancias Y(C j):

Alternativamente, las coordenadas cromáticas y la luminancia de la mezcla se pueden calcular haciendo uso de la bien conocida regla del centro de gravedad, de la forma:
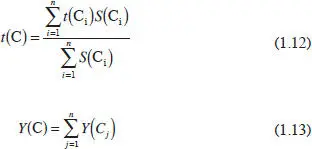
1.6 Color dominante, color complementario, pureza colorimétrica, pureza de excitación
Se llama color dominante (C d) de C (longitud de onda o púrpura) a aquél que mezclado con el blanco del espacio en la proporción adecuada reproduce el color C. Se llama color complementario (C c) de C (longitud de onda o púrpura) a aquél que mezclado con C en la proporción adecuada reproduce el blanco del espacio.
Se denomina pureza colorimétrica (p C) de un color C de luminancia Y(C) y cuyo dominante es C da la relación:

donde T(C) = T(W) + T(C d), y en particular, Y(C) = Y(W) +Y(C d).
Читать дальше

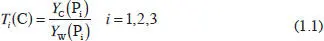
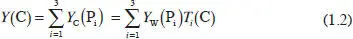
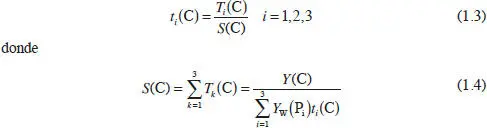
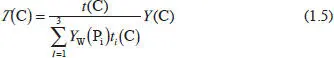
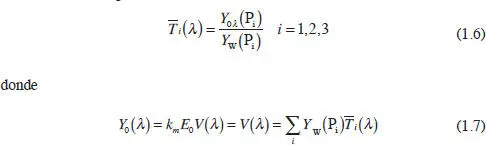 1.4 Cálculo de valores triestímulo a partir de las funciones de igualación
1.4 Cálculo de valores triestímulo a partir de las funciones de igualación