Informationswissenschaft - Theorie, Methode und Praxis / Sciences de l'information - théorie, méthode et pratique

Cela veut dire qu’avant de définir un algorithme de compression, il faut déterminer quel type d’information il s’agit de compresser. Certains algorithmes sont efficaces pour compresser du texte, alors que d’autres sont particulièrement efficaces pour compresser des images. Et parmi les algorithmes efficaces pour compresser les images, certains sont spécifiquement construits pour compresser des images qui représentent du texte en noir/blanc, alors que d’autres sont efficaces pour des images non-textuelles. En effet, tout type de données a un genre de redondance particulier dont il s’agit de tirer profit au mieux. Comme premier exemple, voyons l’algorithme de compression suivant.

Cet algorithme de compression vise typiquement les images en noir/blanc, ou tout autre type d’information dont la représentation numérique comporte une majorité de 0 (et de 1) qui se suivent. Par exemple, le mot 00000000000000000000000000000000111110000000001111000000000000000000000000

pourrait être une partie du codage d’une ligne de pixels dans une image qui représente du texte, en noir, sur un fond blanc. Les 1 représentent les pixels en noir, moins fréquents que les pixels en blanc. L’idée de l’algorithme RLE est de tirer profit des grandes plages de 0 (et de 1), en écrivant

32*05*09*04*24.

Ce mot doit être compris comme signifiant «32 zéros, puis 5 uns, puis 9 zéros, puis 4 uns, puis 24 zéros». En écriture binaire, il devient:

000111111000010000001000 1000001100010111;

sachant que l’on a simplement écrit les nombres 31,4,8,3,23 en binaire sur les 7 derniers bits de chaque groupe de 8 bits (les espaces sont là pour faciliter la lecture de ces groupes). Le premier bit de chaque groupe de 8 bits indique s’il s’agit d’une plage de 0 ou de 1. Il est évident que l’algorithme a effectivement permis d’obtenir un effet de compression: au lieu d’être écrite sur 74 bits, la même information a pu être compressée sur 40 bits.

La faiblesse évidente de cet algorithme réside dans le fait qu’il est incapable de compresser efficacement des mots qui contiennent peu de grandes plages de 0 et de 1. Dans ces cas, l’algorithme augmente la longueur des mots! Un autre point important est que la ligne originale de 0 et de 1 peut aisément être récupérée à partir du mot obtenu par cette méthode de compression. Il n’y a aucune perte d’information dans ce processus.

Très souvent, chaque caractère d’un alphabet est codé avec le même nombre de bits. C’est le cas de la norme de codage ASCII, qui attribue 8 bits à chaque caractère textuel. C’est également le cas lorsque l’on code un ensemble de couleurs sans compression. On emploie fréquemment 24 bits pour coder une couleur. Toutefois, autant dans le cas d’un texte que d’une image, certains caractères apparaissent plus souvent que d’autres. L’idée de David Albert Huffman, en 1952, a été de coder les caractères apparaissant fréquemment avec un nombre plus faible de bits en suivant un processus rigoureux. Ainsi, le caractère apparaissant le plus souvent dans la langue française, «e», sera codé sur un seul bit lorsqu’il s’agit de coder des textes écrits dans cette langue.

Pour un texte particulier, il est possible que ce ne soit pas le caractère «e» qui apparaisse le plus souvent. Pour coder ce texte, il faudrait d’abord calculer les fréquences de chaque caractère pour en déduire le codage approprié. Deux difficultés se présentent dans cette situation. D’une part, pour que le décodeur puisse lire le texte, il faut que le codeur lui transmette la table de codage. 8Cela augmente le poids du fichier et réduit l’efficacité de la compression. D’autre part, le calcul préliminaire des fréquences augmente le temps de codage, ce qui peut être malvenu. Pour éviter ces deux difficultés, c’est une version adaptative du codage de Huffman qui est utilisée. L’idée est de commencer le codage sans utiliser de compression, et ensuite d’adapter la table de codage à chaque caractère codé. Cela se fait de façon à ce que le décodeur puisse reconstruire la table de codage au fur et à mesure du décodage, sans que le codeur n’ait besoin de lui fournir une information.

De la même manière, comme la fréquence d’apparition des couleurs dans une image dépend de celle-ci, c’est un codage adaptatif qui est souvent utilisé pour coder les images.

Ces deux algorithmes ont été pensés pour la transmission de documents en noir (l’information) et blanc (le papier) par fax. Ce sont des standards publiés par l’Union Internationale des Télécommunications (UIT), et leur dénomination officielle est UIT-T T.4 (compression «Groupe 3») et UIT-T T.6 (compression «Groupe 4»). 9

La norme «Groupe 3» consiste en fait en deux algorithmes de compression différents: une compression unidimensionnelle et une compression bidimensionnelle. Le premier de ces algorithmes considère chaque ligne de pixels de manière indépendante des autres lignes, ce qui fait le caractère unidimensionnel de cette méthode. La compression se fait en deux temps. D’abord, il s’agit de procéder à un codage par plages, et ensuite c’est un codage de Huffman qui est appliqué en considérant chaque plage comme un caractère d’un alphabet. Il ne s’agit pas d’un codage adaptatif, mais d’un codage basé sur un set de documents représentatif défini par l’UIT. A titre d’exemple, le tableau de la figure 4est une partie de la table de codage définie par le standard UIT-T T.4.

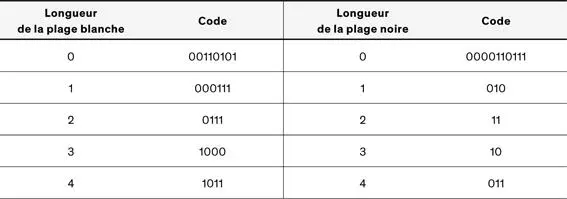
Figure 4: Extrait du Tableau 2/T.4 – Codes de terminaison 10

La compression bidimensionnelle distingue différentes situations. Dans le meilleur des cas, il y a une forte redondance verticale en raison de la nature des documents visés (les documents transmis par fax) et l’idée est de coder une ligne de pixels par rapport à la ligne de pixels qui se trouve immédiatement au-dessus. Lorsqu’une telle redondance n’existe pas sur toute ou une partie d’une ligne, alors c’est le codage unidimensionnel décrit ci-dessus qui est employé. De plus, la compression «Groupe 3» est définie de sorte à pouvoir supporter des erreurs de transmission. Une des mesures prises dans ce cadre est le codage d’une ligne sur deux (ou sur quatre) selon la méthode unidimensionnelle, ce qui permet d’éviter qu’une seule erreur se propage dans toute la suite du document et le rende incompréhensible.

Cette façon de faire limite l’efficacité de la compression puisque l’algorithme renonce volontairement à exploiter la redondance verticale sur tout le document. Pour remédier à ce fait lorsqu’une résistance aux erreurs n’est pas nécessaire, la compression «Groupe 4» reprend le même processus que la compression bidimensionnelle «Groupe 3», en supprimant certains des mécanismes utiles dans des environnements propices aux erreurs. En particulier, l’entier du document est codé suivant le codage bidimensionnel, ce qui permet un taux de compression environ deux fois meilleur.

Une famille d’algorithmes d’un type différent existe. Ce sont les algorithmes basés sur l’utilisation d’un dictionnaire. La stratégie consiste à parcourir le mot à compresser à la recherche de chaînes de caractères qui apparaissent dans un dictionnaire. Lorsqu’une telle chaîne de caractères est trouvée, elle est remplacée par le numéro d’index 11de la chaîne. Par exemple, admettons qu’il existe un dictionnaire pour le français contenant 99 999 mots au plus. Et supposons que le mot: