Para calcular el valor del Número Reproductivo Básico R 0 , se tiene en cuenta la relación del tamaño final de la epidemia, dado en [1]
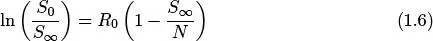
De la ecuación (1.2),
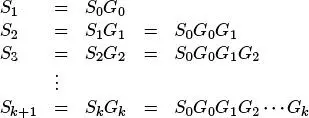
De donde
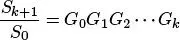
Calculando logaritmo natural en ambos lados de la igualdad se obtiene
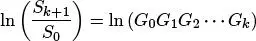
De donde
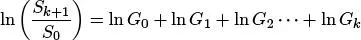
Pero 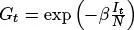 , entonces
, entonces

De donde se obtiene que

Ahora, de la ecuación (1.3)
It +1– (1 – σ ) It = St – StGt
Pero StGt = St +1 , por tanto
It +1– (1 – σ ) It = St – St +1
Sumando desde t = 0 hasta n se obtiene
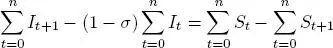
De donde
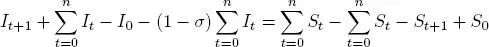
Así que
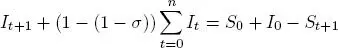
Se tiene que S 0+ I 0= N, además cuando t → ∞, It +1→ 0 , entonces
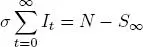
Es decir,
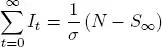
De la ecuación (1.7), se tiene que  , entonces
, entonces
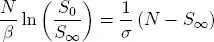
Por lo tanto
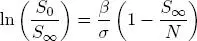
De donde se obtiene la relación del tamaño final de la epidemia dada en (1.6)
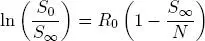
Obteniendo así el Número Reproductivo Básico R 0

Note que β es la probabilidad de una nueva infección y 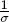 es el tiempo esperado de una persona en estado infeccioso, lo cual da un sentido biológico al Número Reproductivo Básico obtenido.
es el tiempo esperado de una persona en estado infeccioso, lo cual da un sentido biológico al Número Reproductivo Básico obtenido.
A continuación se presentan resultados de algunas simulaciones del modelo realizadas en MatLab.
1.3. Resultados numéricos
En esta sección se presentan resultados de algunas simulaciones para diferentes valores de los parámetros. Sea 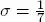 (probabilidad de que un individuo se recupere de manera natural), así que el tiempo esperado de una persona en estado infeccioso será de siete días. Se toman diferentes valores del parámetro β (probabilidad de una nueva infección), obteniendo así diferentes valores de R 0 . Tomamos como valores de β : 0 , 1 , 0 , 3 y 0 , 5 .
(probabilidad de que un individuo se recupere de manera natural), así que el tiempo esperado de una persona en estado infeccioso será de siete días. Se toman diferentes valores del parámetro β (probabilidad de una nueva infección), obteniendo así diferentes valores de R 0 . Tomamos como valores de β : 0 , 1 , 0 , 3 y 0 , 5 .
Las figuras 1.3y 1.4muestran el comportamiento de los individuos susceptibles, infectados y recuperados para R 0= 0 , 7 , R 0= 2 , 1 , y R 0= 3 , 5 . Note que cuando R 0 < 1 ( Figura 1.3) pocas personas son infectadas y la enfermedad desaparece rápidamente. Por el contrario cuando R 0 > 1 ( Figura 1.4) la enfermedad se extiende en la población, llegando a infectar a un buen número de individuos, si no se toman las medidas de control necesarias las cuales pueden incluir tratamiento, vacunación, distanciamiento social, entre otras. A mayor valor de R 0 , un mayor número de individuos será infectado y la enfermedad se propagará con mayor rapidez. Adicionalmente el pico de la epidemia (valor máximo de la curva de infectados) se alcanza más rápido cuando R 0es mayor. En este caso se observa que para R 0= 2 , 1 , el pico se alcanza en el día 63 (ver Figura 1.4, parte superior) mientras que para R 0= 3 , 5 , se alcanza en el día 33 ( Figura 1.4, parte inferior).
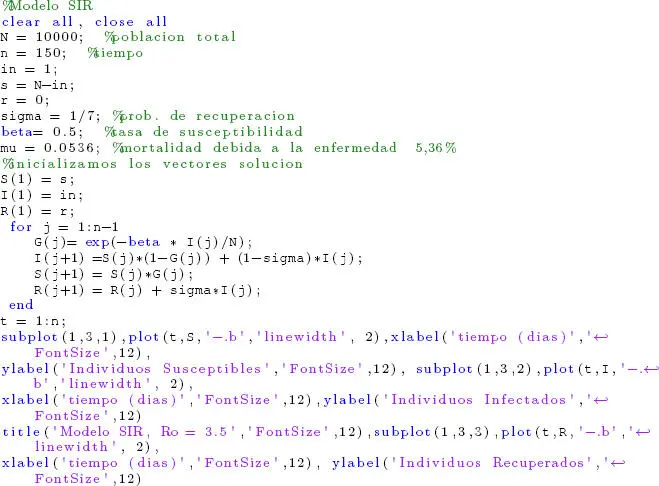
A continuación el código de MatLab con el que se obtuvieron las simulaciones presentadas. Note que el código para el modelo discreto es muy simple, lo cual es una de las ventajas de este tipo de modelos.
Comportamiento de los individuos para R 0= 0,7.
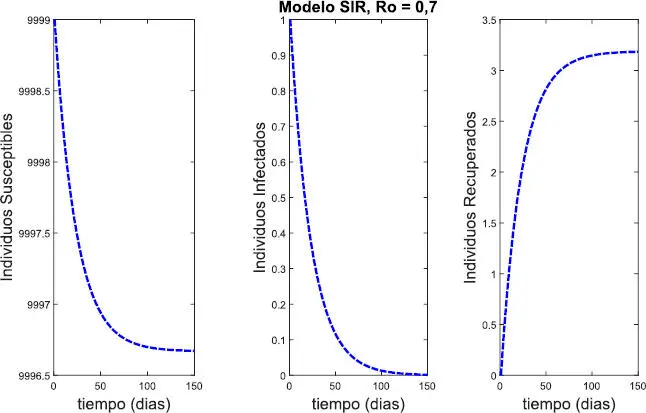
Figura 1.3: Comportamiento de los individuos susceptibles, infectados y recuperados para un valor de R 0= 0 , 7 . Se observa que la enfermedad rápidamente desaparece. No se da un brote puesto que R 0 < 1.
Finalmente, la Figura 1.5muestra el número acumulado de individuos infectados para los valores dados de R 0, evidenciando además el tamaño final de la epidemia; es decir, que porcentaje de la población se infectará durante el transcurso de la misma. Se observa que en el primer caso R 0= 0 , 7 , el número total de infectados tiende a cero, tal como se había indicado para valores de R 0 < 1 . En el caso de R 0= 2 , 1 el 82 % de la población se infectaría si no se tomara ninguna medida de control. Para R 0= 3 , 5 el porcentaje de la población que se podría infectar sería del 96 % .
Читать дальше

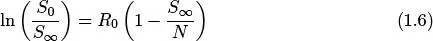
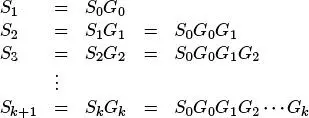
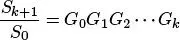
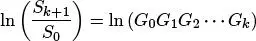
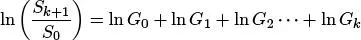
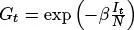 , entonces
, entonces

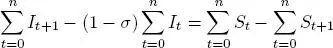
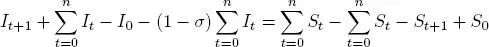
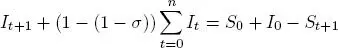
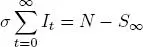
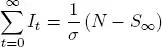
 , entonces
, entonces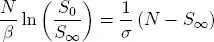
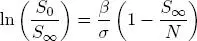
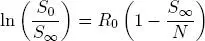

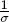 es el tiempo esperado de una persona en estado infeccioso, lo cual da un sentido biológico al Número Reproductivo Básico obtenido.
es el tiempo esperado de una persona en estado infeccioso, lo cual da un sentido biológico al Número Reproductivo Básico obtenido.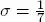 (probabilidad de que un individuo se recupere de manera natural), así que el tiempo esperado de una persona en estado infeccioso será de siete días. Se toman diferentes valores del parámetro β (probabilidad de una nueva infección), obteniendo así diferentes valores de R 0 . Tomamos como valores de β : 0 , 1 , 0 , 3 y 0 , 5 .
(probabilidad de que un individuo se recupere de manera natural), así que el tiempo esperado de una persona en estado infeccioso será de siete días. Se toman diferentes valores del parámetro β (probabilidad de una nueva infección), obteniendo así diferentes valores de R 0 . Tomamos como valores de β : 0 , 1 , 0 , 3 y 0 , 5 .












