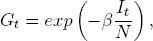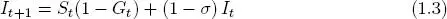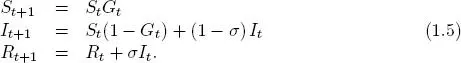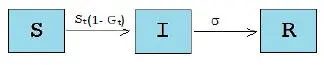Paula Andrea González Parra - Modelos discretos en epidemiología

Teniendo en cuenta que muchas enfermedades afectan de manera diferente a algunos grupos de la población, a veces de acuerdo a la edad de los individuos, otras como el caso del COVID-19 presentan manifestaciones más severas en poblaciones con enfermedades de base; ciertos grupos pueden ser más vulnerables, por tanto se introduce en el Capítulo 5un modelo en el que la población es dividida en grupos, los cuales pueden definirse de acuerdo a la edad, grado de susceptibilidad, etc. En nuestras simulaciones, consideramos el caso de dos y tres grupos para diferentes escenarios. En particular, cuando la población es dividida en tres grupos, se compara cómo deben ser aplicadas las estrategias en el caso de la influenza estacional en contraste con la pandemia de influenza AH1N1, para esto se dividió la población colombiana por edades, teniendo en cuenta datos del Departamento Nacional de Estadistica (DANE) [19].

Finalmente en el Capítulo 6se formula un modelo de propagación del COVID-19, en el cual se considera la presencia de individuos asintomáticos o con síntomas leves, ya que esto puede explicar la alta propagación de esta enfermedad. Se comparan resultados del modelo con datos estadísticos de la ciudad de Santiago de Cali [14]. En el modelo se incorpora una función que representa distanciamiento social teniendo en cuenta la cuarentena obligatoria decretada por el Gobierno en el mes de marzo de 2020, esta función es modificada teniendo en cuenta la apertura paulatina de ciertos sectores de la economía. Se muestra cómo estas políticas han ayudado a mitigar un poco el impacto de la enfermedad.

Capítulo 1

Modelo SIR

Una de las contribuciones más importantes en epidemiología matemática es el modelo compartamental propuesto por Kermack y McKendrick formulado en 1927 [1, 2, 3, 4], el cual es un modelo continuo basado en el flujo de individuos entre diferentes clases.

En particular es bien conocido el clásico modelo SIR, en el que la población total es dividida en Susceptibles (personas que no han contraido la enfermedad y podrían ser infectados), Infectados (personas que han adquirido la enfermedad y pueden transmitirla a otros individuos) y Removidos o Recuperados (individuos que estuvieron infectados y ya se recuperaron de la enfermedad). En la Figura 1.1se muestra el diagrama de flujo de la dinámica de la enfermedad para el modelo continuo SIR. En este diagrama cada compartimento representa una clase de individuos; Susceptibles (S) - Infectados (I) - Recuperados (R), las personas se mueven de un compartimento a otro cuando cambia su estado en la epidemia.

Diagrama modelo continuo SIR

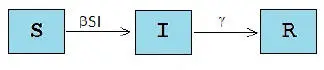
Figura 1.1: Diagrama de flujo compartamental para el modelo SIR. Los individuos se mueven de un compartimento a otro cuando cambia su estado epidemiológico. Un susceptible (S) pasa a ser infectado (I) o un infectado (I) pasa a ser recuperado (R).

El modelo está dado por el sistema de ecuaciones diferenciales:

En este modelo no se tienen en cuenta efectos demográficos; es decir, no hay nacimientos ni muertes, tampoco se considera mortalidad debido a la enfermedad. La transmisión de la enfermedad se da teniendo en cuenta la ley de acción de masas, así pues, el término βSI representa el número de individuos que pasa de la clase S a la clase I.

1.1.Presentación del modelo discreto SIR

En los últimos años se ha incrementado el interés en el uso de modelos discretos para estudiar la dinámica de las enfermedades transmisibles [1, 5, 6, 7, 8], sin embargo no son muchos los estudios en los que se consideran modelos discretos. Aunque matemáticamente son un poco más complejos, los resultados son más fáciles de comparar con los datos experimentales dado que los datos son obtenidos en intervalos discretos de tiempo (días, semanas, meses, entre otros).

Se presenta a continuación la versión discreta del modelo SIR. Para esto se siguen las ideas presentadas en [20, 21], de manera similar a la versión continua presentada, no se tienen en cuenta nacimientos y muertes por causas naturales, ya que se considera un único brote de la enfermedad. En el modelo, el subindice t es utilizado para denotar el número de individuos de cada clase en el tiempo t ; es decir, St, It, y Rt, representan el número de susceptibles, infectados y recuperados en el tiempo t, para t en el intervalo [0 , n ] , donde n denota el tiempo final de un brote único de la enfermedad.

La fracción de individuos susceptibles al tiempo t que permanecen susceptibles en el tiempo t + 1 está dado por la función

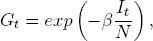
donde β representa la probabilidad de una nueva infección, por tanto el número de individuos susceptibles en el día t + 1 está dado por la ecuación

Así pues, 1 Gt representa la fracción de individuos que eran suscetibles y son infectados en el tiempo t + 1. No se consideraron muertes debidas a la enfermedad; se asume que la probalilidad de que un individuo se recupere de manera natural está dada por σ (por generación). Por tanto el número de individuos infectados el día t + 1 está dado por los que eran susceptibles el día t y se infectaron, más los que estaban infectados el día t y no se recuperaron, así:

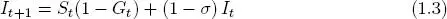
Finalmente el número de individuos recuperados el día t +1 está dado por los que ya estaban recuperados el día t más los que estaban infectados y ya se recuperaron.

Teniendo en cuenta las consideraciones y definiciones dadas, el modelo está dado por el siguiente sistema de ecuaciones en diferencias:

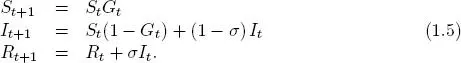
La Figura 1.2muestra una representación de la dinámica de la enfermedad.

Diagrama modelo discreto SIR

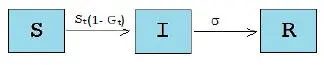
Figura 1.2: Diagrama de flujo compartamental para el modelo discreto SIR.

A continuación se presenta el Número Reproductivo Básico R 0 , el cual se define como el número de casos secundarios que un único individuo infectado puede producir en una población de individuos susceptibles.

1.2. Número Reproductivo Básico R0