John O'Brien - Earth Materials
Здесь есть возможность читать онлайн «John O'Brien - Earth Materials» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Earth Materials
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 100
- 1
- 2
- 3
- 4
- 5
Earth Materials: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Earth Materials»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Earth Materials,
Earth Materials,
Earth Materials — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Earth Materials», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
Source : Wenk and Bulakh (2004). © Cambridge University Press.
4.3 TWO‐DIMENSIONAL MOTIFS AND LATTICES (MESHES)
The symmetry of three‐dimensional crystals can be quite complex. Understanding symmetry in two dimensions provides an excellent basis for understanding the increased complexity that characterizes three‐dimensional symmetries. It also provides a basis for learning to visualize planes of constituents within three‐dimensional crystals. Being able to visualize and reference lattice planes is of the utmost importance in describing cleavage and crystal faces and in the identification of minerals by X‐ray diffraction methods.
4.3.1 Plane point groups
As discussed earlier, any fundamental unit of two‐dimensional pattern, or motif, can be repeated by various symmetry operations to produce a larger two‐dimensional pattern. All two‐dimensional motifs that are consistent with the generation of long‐range two‐dimensional arrays can be assigned to one of ten plane point groupsbased on their unique plane point group symmetry ( Figure 4.8). Using the symbolic language discussed in the previous section on symmetry, the ten plane point groups are 1, 2, 3, 4, 6, m, 2mm, 3m, 4mm, and 6mm. The numbers refer to axes of rotation that are perpendicular to the plane (or page); the m refers to mirror planes perpendicular to the page. The first m refers to a set of mirror planes that is repeated by the rotational symmetry and the second m to a set of mirror planes that bisects the first set. Note that the total number of mirror planes is the same as the number associated with its rotational axis (e.g., 3m has three mirror planes and 6mm has six mirror planes).
4.3.2 Plane lattices and unit meshes
As discussed previously, any motif can be represented by a point called a node. Points or nodes can be translated some distance in one direction by a unit translation vector t aor t 1to produce a line of nodes or motifs. Nodes can also be translated some distances in two directions t aand t bor t 1and t 2to produce a two‐dimensional array of points called a plane mesh or plane net. Simple translation of nodes in two directions produces five basic types of two‐dimensional patterns ( Figure 4.9). The smallest units of such meshes, which contain the unit translation vectors and at least one node, are called unit meshes (unit nets). Unit meshes contain all the information necessary to produce the larger two‐dimensional pattern. They contain only translation symmetry information. The five basic types of unit mesh are classified on the basis of (1) the unit translation vector lengths (equal or unequal), the angles between them (90°, 60°, and 120° or none of these) and (2) whether they have nodes only at the corners (primitive = p) or have an additional node in the center (c) of the mesh.
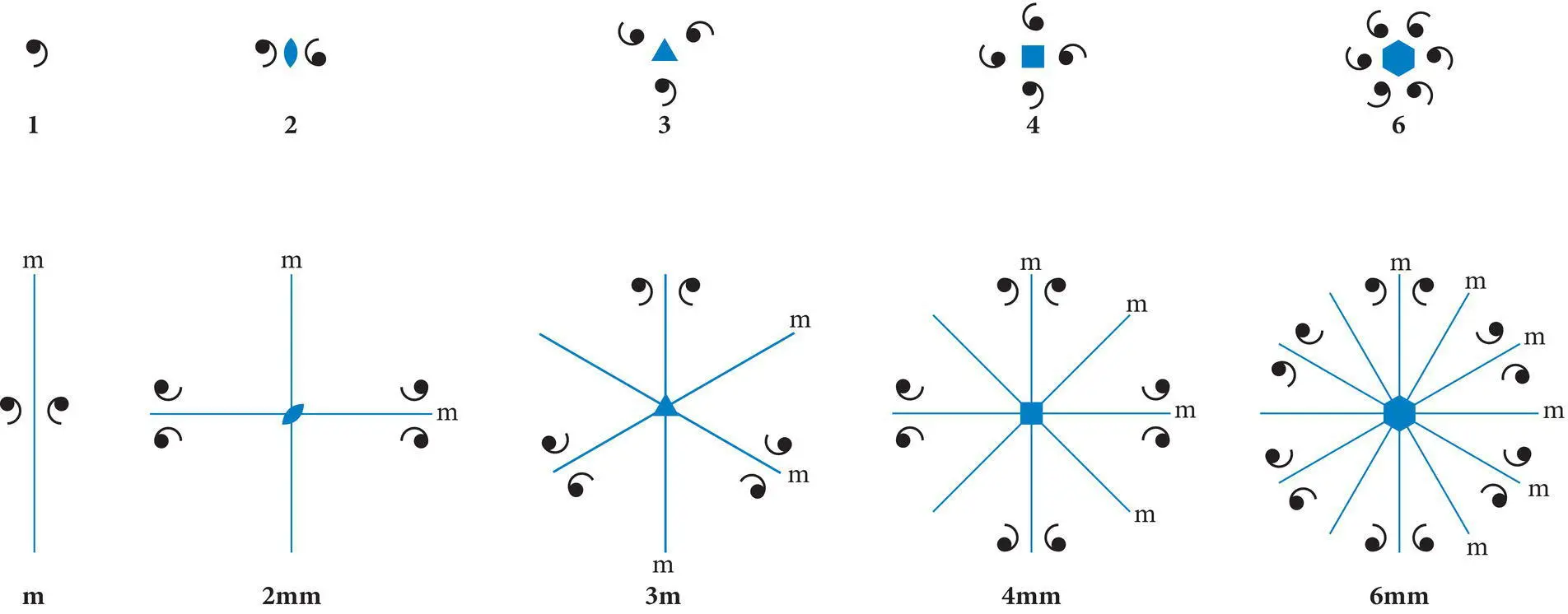
Figure 4.8 The 10 plane point groups defined by rotational and reflection symmetry.
Source : Klein and Hurlbut (1985). © John Wiley & Sons.
Square unit meshes( Figure 4.9a) are primitive and have equal unit translation vectors at 90° angles to each other (p, t a= t b, γ = 90°). Primitive rectangular unit meshes( Figure 4.9b) differ in that, although the unit translation vectors intersect at right angles, they are of unequal lengths (p, t a≠ t b, γ = 90°). Diamond unit mesheshave equal unit translation vectors that intersect at angles other than 60°, 90° or 120°. Diamond lattices can be produced and represented by primitive diamond unit meshes(p, t a= t b, γ ≠ 60°, 90° or 120°). They can also be produced by the translation of centered rectangular unit meshes( Figure 4.9c) in which the two unit mesh sides are unequal, the angle between them is 90°, and there is a second node in the center of the mesh (c, t a≠ t b, γ = 90°). In a centered rectangular mesh there is a total content of two nodes = two motifs. If one looks closely, one may see evidence for glide reflection in the centered rectangular mesh and/or the larger diamond lattice. The hexagonal unit mesh( Figure 4.9d) is a special form of the primitive diamond mesh because, although the unit translation vectors are equal, the angles between them are 60° and 120° (p, t a= t b, γ = 120°). Rotation through 120 ogenerates three such unit meshes which combine to produce a larger pattern with hexagonal symmetry. Oblique unit meshes( Figure 4.9e) are primitive and are characterized by unequal unit translation vectors that intersect at angles that are not 90°, 60° or 120° (p, t a≠ t b, γ ≠ 90°, 60° or 120°) and produce the least regular, least symmetrical two‐dimensional lattices. The arrays of nodes on planes within minerals always correspond to one of these basic patterns.
4.3.3 Plane lattice groups
When the ten plane point groups are combined with the five unit meshes in all ways that are compatible, a total of 17 plane lattice groupsare recognized on the basis of the total symmetry of their plane lattices. Note that these symmetries involve translation‐free symmetry operations that include rotation and reflection, translation and compound symmetry operations such as glide reflection. Table 4.2summarizes the 17 plane lattice groups and their symmetries. Primitive lattices are denoted by “P” and centered lattices by “C.” Axes of rotation for the entire pattern perpendicular to the plane are noted by 1, 2, 3, 4, and 6. Mirror planes perpendicular to the plane are denoted by “m”; glide planes perpendicular to the plane are denoted by “g.”
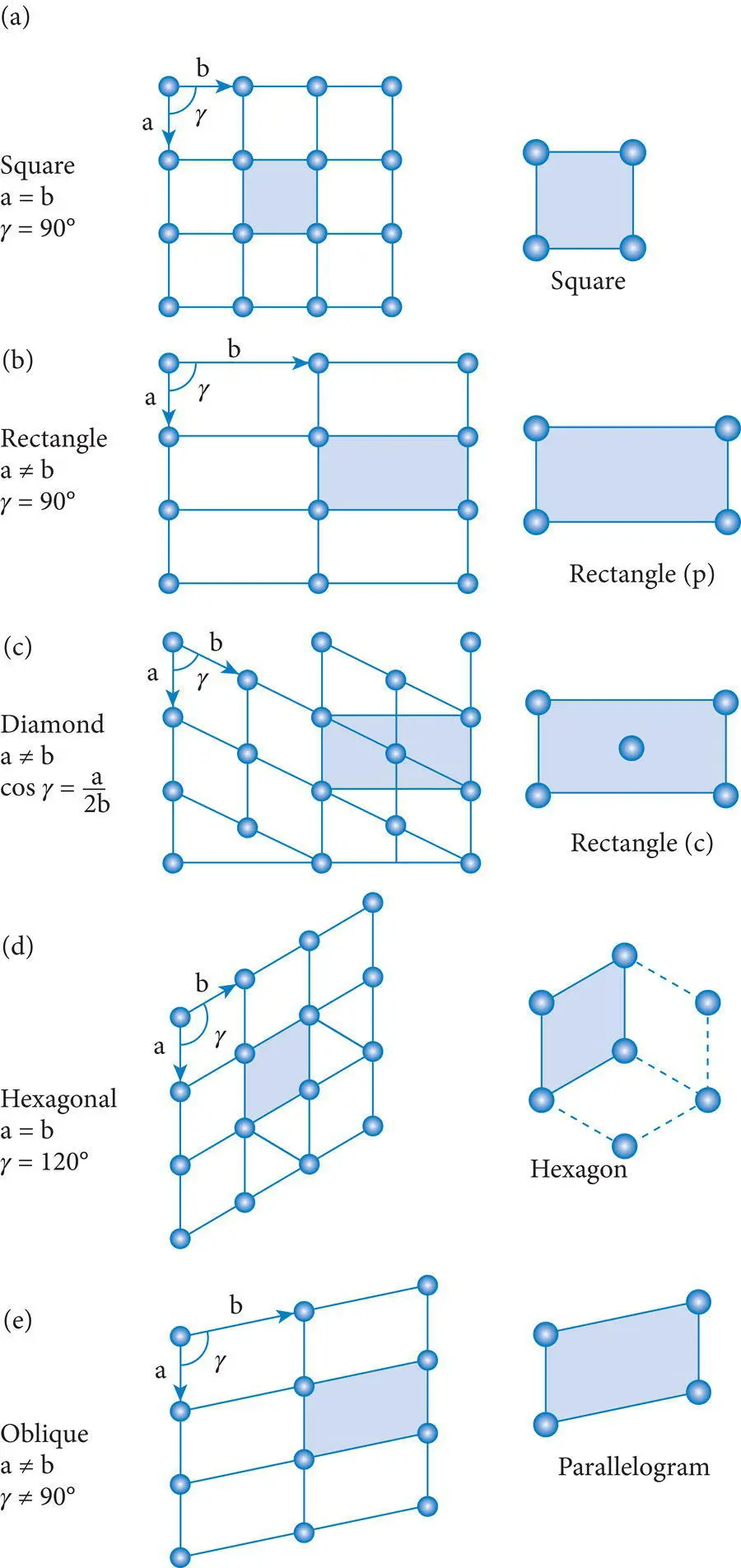
Figure 4.9 The five principal types of meshes or nets and their unit meshes (shaded gray): (a) square, (b) primitive rectangle, (c) diamond or centered rectangle, (d) hexagonal, (e) oblique.
Source : Nesse (2016). © Oxford University Press.
Table 4.2 The 17 plane lattice groups and the unique combination of point group and unit mesh that characterizes each.
| Lattice | Point group | Plane group |
|---|---|---|
| Oblique (P) | 1 | P1 |
| 2 | P2 | |
| Rectangular (P and C) | m | Pm |
| Pg | ||
| Cm | ||
| 2mm | P2mm | |
| P2mg | ||
| P2gg | ||
| C2mm | ||
| Square (P) | 4 | P4 |
| 4mm | P4mm | |
| P4gm | ||
| Hexagonal (P) (rhombohedral) | 3 | P3 |
| 3m | P3m1 | |
| P3lm | ||
| Hexagonal (P) (hexagonal) | 6 | P6 |
| 6mm | P6mm |
The details of plane lattice groups are well documented (see for example, Klein and Dutrow 2007), but are beyond the introductory material in this text.
4.4 THREE‐DIMENSIONAL MOTIFS AND LATTICES
Minerals are three‐dimensional Earth materials with three‐dimensional crystal lattices. The fundamental units of pattern in any three‐dimensional lattice are three‐dimensional motifsthat can be classified according to their translation‐free symmetries. These three‐dimensional equivalents of the two‐dimensional plane point groups are called space point groups.
Читать дальшеИнтервал:
Закладка:
Похожие книги на «Earth Materials»
Представляем Вашему вниманию похожие книги на «Earth Materials» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Earth Materials» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.












