John O'Brien - Earth Materials
Здесь есть возможность читать онлайн «John O'Brien - Earth Materials» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Earth Materials
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 100
- 1
- 2
- 3
- 4
- 5
Earth Materials: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Earth Materials»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Earth Materials,
Earth Materials,
Earth Materials — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Earth Materials», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
Space point groups can be represented by nodes. These nodes can be translated to produce three‐dimensional patterns of points called space lattices. Space lattices are the three‐dimensional equivalents of plane nets or meshes. By analogy with unit meshes or nets, we can recognize the smallest three‐dimensional units, called unit cells, which contain all the information necessary to produce the three‐dimensional space lattices. In this section, we will briefly describe the space point groups, after which we will introduce Bravais lattices, unit cells, and their relationship to the six (or seven) major crystal systems to which minerals belong.
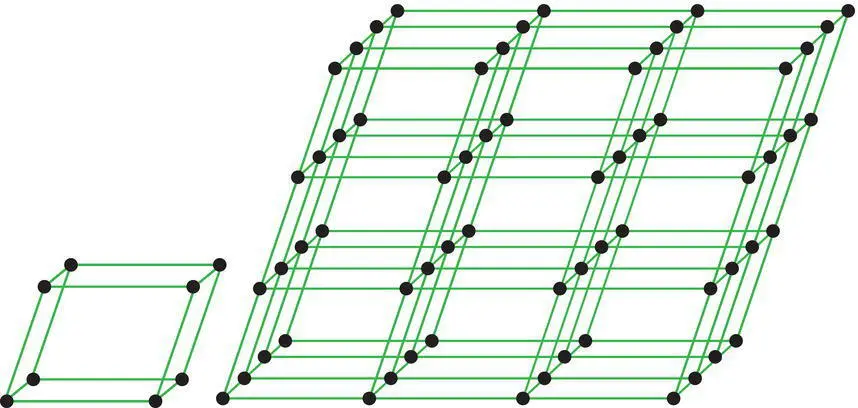
Figure 4.10 A primitive unit cell and a long‐range space point lattice that results from its repetition by symmetry operations in three dimensions.
4.4.1 Space point groups
In minerals, the fundamental motifs are parts of clusters of three‐dimensional coordination polyhedra sufficient to establish the composition of the mineral. When these are repeated in three dimensions during mineral growth, they produce the long‐range order characteristic of crystalline substances ( Figure 4.10). Like all fundamental units of pattern, these three‐dimensional motifs can be classified on the basis of their translation‐free symmetries.
Only 32 different three‐dimensional motif symmetries exist. These define 32 space point groups, each with unique space point group symmetry. In minerals, the 32 crystal classes– to one of which all minerals belong – correspond to the 32 space point group symmetries of the mineral's three‐dimensional motif. That the crystal classes were originally defined on the basis of the external symmetry of mineral crystals is another example of the fact that the external symmetry of minerals reflects the internal symmetry of their constituents. The 32 crystal classes belong to 6 (or 7) crystal systems, each with its own characteristic symmetry. Table 4.3summarizes the crystal systems, the symmetries of the 32 space point groups or crystal classes and their names, which are based on general crystal forms. It is important to remember that a crystal cannot possess more symmetry than that of the motifs of which it is composed. However, it can possess less, depending on how the motifs are arranged and how the crystal developed during growth.
4.4.2 Bravais lattices, unit cells, and crystal systems
As noted earlier, any motif can be represented by a point called a node. Nodes, and the motifs they represent, can also be translated in three directions (t a, t b, and t c) to produce three‐dimensional space point lattices and unit cells ( Figure 4.10).
Unit cells are the three‐dimensional analogs of unit meshes. A unit cellis a parallelepiped whose edge lengths and volume are defined by the three unit translation vectors (t a, t b, and t c). The unit cell is the smallest unit that contains all the information necessary to reproduce the mineral by three‐dimensional symmetry operations. Unit cells may be primitive (P), in which case they have nodes only at their corners and a total content of one node (=one motif). Non‐primitive cellsare multiple because they contain extra nodes in one or more faces (A, B, C or F) or in their centers (I) and possess a total unit cell content of more than one node or motif.
Unit cells bear a systematic relationship to the coordination polyhedra and packing of atoms that characterize mineral structures, as illustrated by Figure 4.11.
In 1850, Bravais recognized that only 14 basic types of three‐dimensional translational point lattices exist; these are known as the 14 Bravais space point lattices(Klein and Hurlbut 1985) and define 14 basic types of unit cells. The 14 Bravais lattices are distinguished on the basis of (1) the magnitudes of the three unit translation vectors t a, t b, and t cor more simply a, b, and c, (2) the angles (alpha, beta, and gamma) between them, where (α = b Λ c; β = c Λ a; γ = a Λ b), and (3) whether they are primitive lattices or some type of multiple lattice. Figure 4.12illustrates the 14 Bravais space point lattices.
The translational symmetry of every mineral can be represented by one of the 14 basic types of unit cells. Each unit cell contains one or more nodes that represent motifs and contains all the information necessary to characterize chemical composition. Each unit cell also contains the rules according to which motifs are repeated by translation; the repeat distances, given by t a= a, t b= b, t c= c, and directions, given by angles α, β, and γ. The 14 Bravais lattices can be grouped into crystal systemson the basis of the relative dimensions of the unit cell edges (a, b, and c) and the angles between them (α, β, and γ). These six (or seven if the hexagonal system is divided into trigonal and hexagonal) systems in which all minerals crystallize. These include the isometric (cubic), tetragonal, orthorhombic, monoclinic, triclinic,and hexagonal systems. The latter is subdivided into the hexagonal division or system and the trigonal (rhombohedral) division or system. Table 4.4summarizes the characteristics of the Bravais lattices in the major crystal systems.
Table 4.3 The six crystal systems and 32 crystal classes, with their characteristic symmetry and crystal forms.
| System | Crystal class | Class symmetry | Total symmetry |
|---|---|---|---|
| Isometric | Hexoctahedral |  |
3A 4, 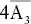 , 6A 2, 9m , 6A 2, 9m |
| Hextetrahedral | 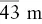 |
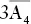 , 4A 3, 6m , 4A 3, 6m |
|
| Gyroidal | 432 | 3A 4, 4A 3, 6A 2 | |
| Diploidal | 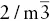 |
3A 2, 3m, 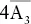 |
|
| Tetaroidal | 23 | 3A 2, 4A 3 | |
| Tetragonal | Ditetragonal–dipyramidal | 4/m2/m2/m | i, 1A 4, 4A 2, 5m |
| Tetragonal–scalenohedral | 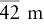 |
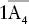 , 2A 2, 2m , 2A 2, 2m |
|
| Ditetragonal–pyramidal | 4mm | 1A 4, 4m | |
| Tetragonal–trapezohedral | 422 | 1A 4, 4A 2 | |
| Tetragonal–dipyramidal | 4/m | i, 1A 4, 1m | |
| Tetragonal–disphenoidal | 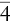 |
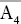 |
|
| Tetragonal–pyramidal | 4 | 1A 4 | |
| Hexagonal(hexagonal) | Dihexagonal–dipyramidal | 6/m2/m2/m | i, 1A 6, 6A 2, 7m |
| Ditrigonal–dipyramidal | 6m2 | 1A 6, 3A 2, 3m | |
| Dihexagonal–pyramidal | 6mm | 1A 6, 6m | |
| Hexagonal–trapezohedral | 622 | 1A 6, 6A 2 | |
| Hexagonal–dipyramidal | 6/m | i, 1A 6, 1m | |
| Trigonal–dipyramidal | 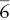 |
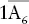 |
|
| Hexagonal–pyramidal | 6 | 1A 6 | |
| Hexagonal (rhombohedral or trigonal) | Hexagonal–scalenohedral | 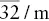 |
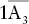 , 3A 2, 3m , 3A 2, 3m |
| Ditrigonal–pyramidal | 3m | 1A 3, 3m | |
| Trigonal–trapezohedral | 32 | 1A 3, 3A 2 | |
| Rhombohedral | 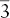 |
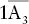 |
|
| Trigonal–pyramidal | 3 | 1A 3 | |
| Orthorhombic | Rhombic–dipyramidal | 2/m2/m2/m | i, 3A 2, 3m |
| Rhombic–pyramidal | mm2 | 1A 2, 2m | |
| Rhombic–disphenoidal | 222 | 3A 2 | |
| Monoclinic | Prismatic | 2/m | i, 1A 2, 1m |
| Sphenoidal | 2 | 1A 2 | |
| Domatic | m | 1m | |
| Triclinic | Pinacoidal | 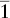 |
i |
| Pedial | 1 | None |
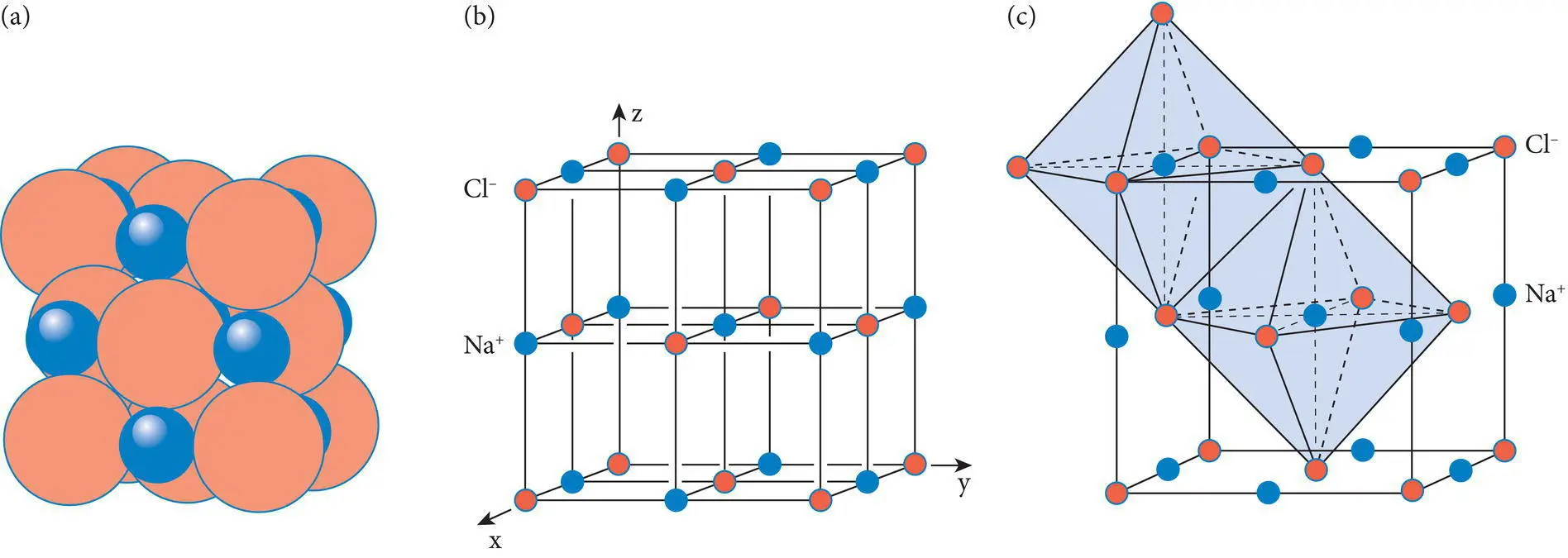
Figure 4.11 Relationship between (a) atomic packing, (b) a unit cell, and (c) octahedral coordination polyhedra in halite (NaCl).
Читать дальшеИнтервал:
Закладка:
Похожие книги на «Earth Materials»
Представляем Вашему вниманию похожие книги на «Earth Materials» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Earth Materials» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.












