John O'Brien - Earth Materials
Здесь есть возможность читать онлайн «John O'Brien - Earth Materials» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Earth Materials
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 100
- 1
- 2
- 3
- 4
- 5
Earth Materials: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Earth Materials»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Earth Materials,
Earth Materials,
Earth Materials — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Earth Materials», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
Rotation
Motifs can also be repeated by non‐translational symmetry operations. Many patterns can be repeated by rotation (n). Rotation (n)is a symmetry operation that involves the rotation of a pattern about an imaginary line or axis, called an axis of rotation (A), in such a way that every component of the pattern is perfectly repeated one or more times during a complete 360° rotation. The symbol “n” denotes the number of repetitions that occur during a complete rotation. Figure 4.3uses triangle motifs to depict the major types of rotational symmetry (n) that occur in minerals and other crystals. The axis of rotation for each motif is perpendicular to the page. Table 4.1summarizes the major types of rotational symmetry.
Table 4.1 Five common axes of rotational symmetry in minerals.
| Type | Symbolic notation | Description |
|---|---|---|
| Onefold axis of rotation | (1 or A 1) | Any axis of rotation about which the motif is repeated only once during a 360° rotation ( Figure 4.3(1)) |
| Twofold axis of rotation | (2 or A 2) | Motifs repeated every 180° or twice during a 360° rotation ( Figure 4.3(2)) |
| Threefold axis of rotation | (3 or A 3) | Motifs repeated every 120° or three times during a complete rotation ( Figure 4.3(3)) |
| Fourfold axis of rotation | (4 or A 4) | Motifs repeated every 90° or four times during a complete rotation ( Figure 4.3(4)) |
| Sixfold axis of rotation | (6 or A 6) | Motifs repeated every 60° or six times during a complete rotation ( Figure 4.3(5)) |
Reflection
Reflection is as familiar to us as our own reflections in a mirror or that of a tree in a still body of water. It is also the basis for the concept of bilateral symmetry that characterizes many organisms ( Figure 4.4). Yet it is a symmetry operation that is somewhat more difficult for most people to visualize than rotation. Reflectionis a symmetry operation in which every component of a pattern is repeated by reflection across a plane called a mirror plane(m). Reflection occurs when each component is repeated by equidistant projection perpendicular to the mirror plane. Reflection retains all the components of the original motif but changes its “handedness”; the new motifs produced by reflection across a mirror plane are mirror images of each other ( Figure 4.4). Symmetry operations that change the handedness of motifs are called enantiomorphic operations.
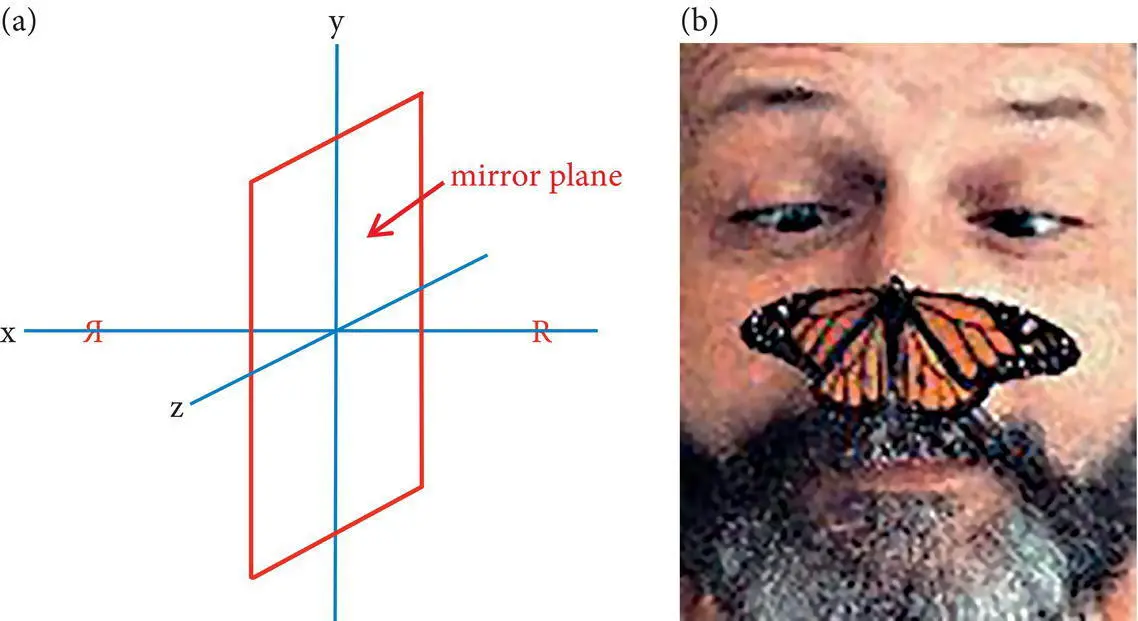
Figure 4.4Two‐ and three‐dimensional motifs that illustrate the concept of reflection across a plane of mirror symmetry (m). (a) Mirror image of the letter “R”. (b) Bilateral symmetry of a butterfly; the two halves are nearly, but not quite, perfect mirror images of each other.
Source : Image from butterflywebsite.com. © Mikula Web Solutions.
One test for the existence of a mirror plane of symmetry is that all components of the motifs on one side of the plane are repeated at equal distances on the other side of the plane along projection lines perpendicular to the plane. If this is not true, the plane is not a plane of mirror symmetry.
Inversion
Inversion is perhaps the most difficult of the simple symmetry operations to visualize. Inversioninvolves the repetition of motifs by inversion through a point called a center of inversion (i). Inversion occurs when every component of a pattern is repeated by equidistant projection through a common point or center of inversion. The two “letters” in Figure 4.5illustrates this enantiomorphic symmetry operation and shows the center through which inversion occurs. In some symbolic notations centers of inversion are symbolized by (c) rather than (i).
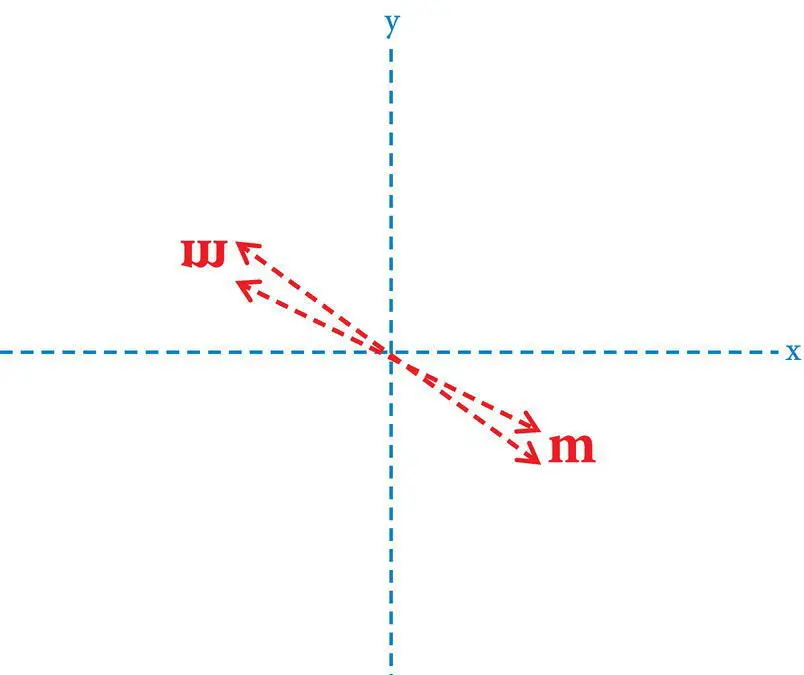
Figure 4.5 Inversion through a center of symmetry (i) illustrated by the letter “m” repeated by inversion through a center (inversion point).
One test for the existence of a center of symmetry is that all the components of a pattern are repeated along straight lines that pass through a common center and are repeated at equal distances from that center. If this is not the case, the pattern does not possess a center of symmetry.
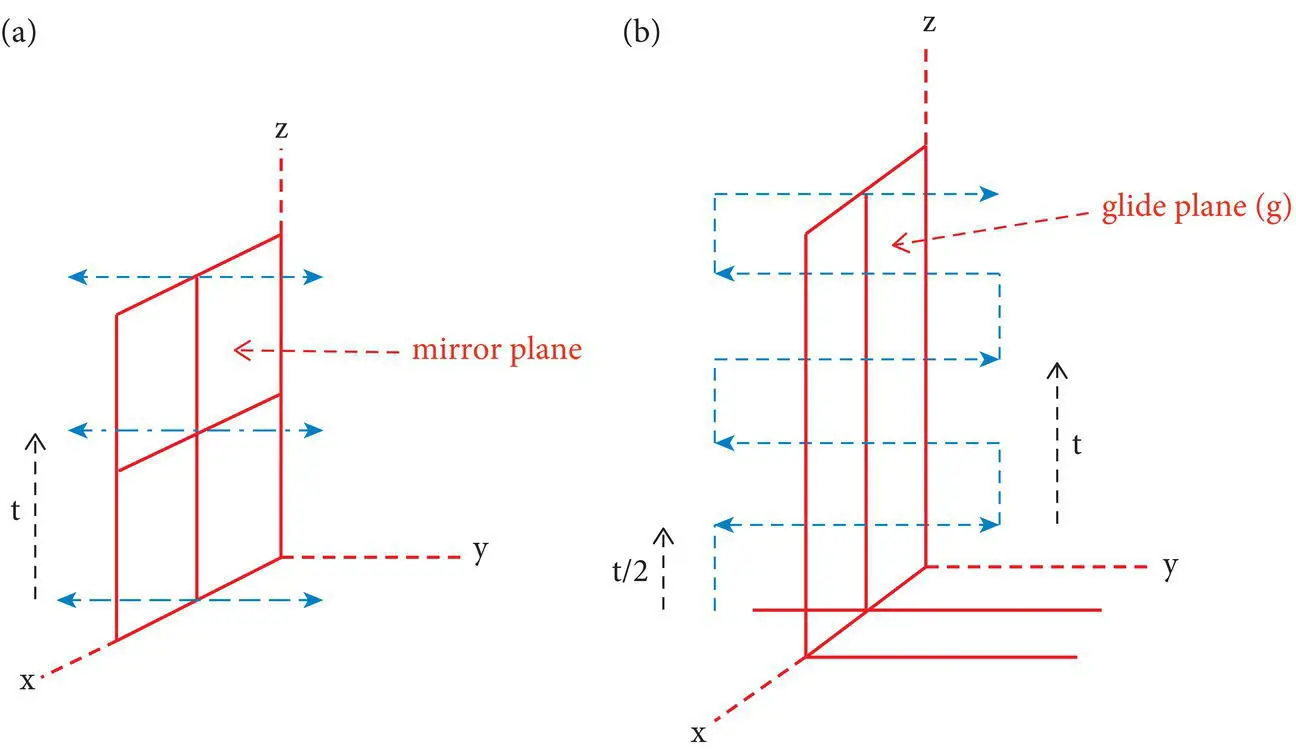
Figure 4.6 (a) Mirror plane (m) with the translation vector (t), contrasted with (b) a glide plane (g) with the translation vector (t/2) combined with mirror reflection.
4.2.2 Compound symmetry operations
Three other symmetry operations exist. However, unlike those discussed so far, they are compound symmetry operations that combine two simple symmetry operations. Glide reflection(g) is a symmetry operation that combines translation (t) parallel to a mirror plane (m) with reflection across the mirror plane to produce a glide plane ( Figure 4.6).
Rotoinversion(n –) is an operation that combines rotation about an axis with inversion through a center to produce an axis of rotoinversion ( Figure 4.7). Figure 4.7b illustrates an axis of fourfold rotoinversion ( 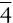 ) in which the motif is repeated after 90° rotation followed by inversion through a center so that it is repeated four times by rotoinversion during a 360° rotation. Axes of twofold rotoinversion (
) in which the motif is repeated after 90° rotation followed by inversion through a center so that it is repeated four times by rotoinversion during a 360° rotation. Axes of twofold rotoinversion ( 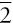 ) are unique symmetry operations, whereas axes of threefold rotoinversion (
) are unique symmetry operations, whereas axes of threefold rotoinversion ( 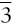 ) are equivalent to a threefold axis of rotation and a center of inversion (3i), and axes of sixfold rotoinversion (
) are equivalent to a threefold axis of rotation and a center of inversion (3i), and axes of sixfold rotoinversion ( 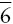 ) are equivalent to a threefold axis of rotation perpendicular to a mirror plane (3/m).
) are equivalent to a threefold axis of rotation perpendicular to a mirror plane (3/m).
Screw rotation(n a) is a symmetry operation that combines translation parallel to an axis with rotation about the axis. This is similar to what occurs when a screw is inserted into a wall ( Figure 4.7c). Much more detailed treatments of the various types of compound symmetry operations can be found in Klein and Dutrow (2007), Wenk and Bulakh (2016) or Nesse (2016).
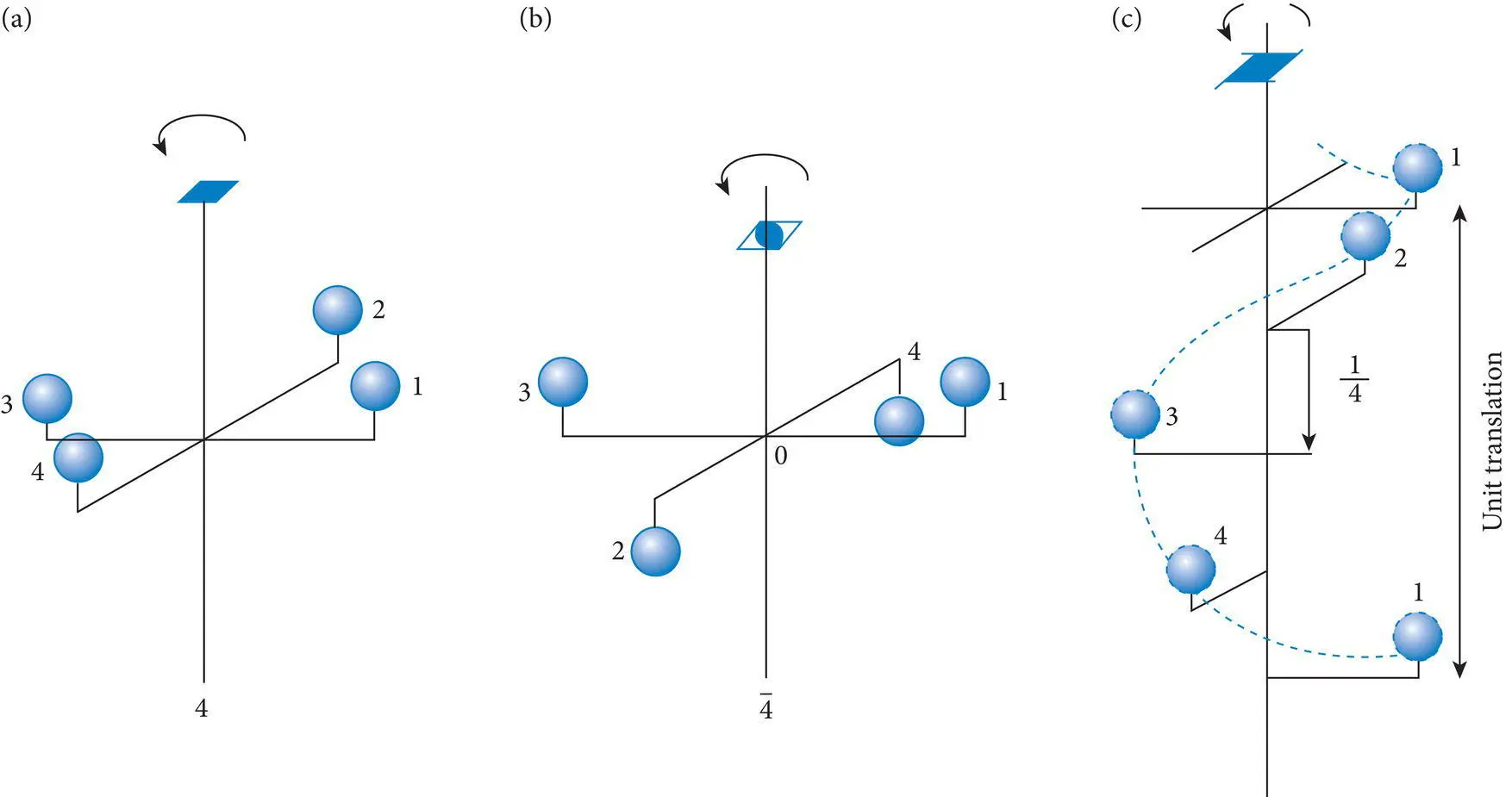
Figure 4.7 (a) An axis of fourfold rotation (4). This contrasts with (b) an axis of fourfold rotoinversion ( 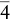 ) that combines rotation with inversion every 90°, and (c) a fourfold screw axis (4 1) that combines translation with 90° rotations every one‐fourth translation.
) that combines rotation with inversion every 90°, and (c) a fourfold screw axis (4 1) that combines translation with 90° rotations every one‐fourth translation.
Интервал:
Закладка:
Похожие книги на «Earth Materials»
Представляем Вашему вниманию похожие книги на «Earth Materials» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Earth Materials» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.












