Reproducibility.If you and a classmate both ran the code above exactly as presented, you would get different estimates of the probability via the simulation. This is due to having different random numbers in your simulations. Some readers may know that computer random number generators are really only pseudorandom. The computer is using an algorithm that generates numbers which behave like random numbers would. It turns out that this is actually a plus when writing code or doing simulations in the sense that you can make the computer regenerate the same random numbers by “setting a seed.” You can think of a seed as telling the computer where to start the algorithm for generating the random numbers. Then, if anyone else runs the code (including the seed), they would get the same result that you did with that seed (provided they have the same software and version). In Rthis is accomplished with the command
> set.seed(360)
where any number can be used as the input. We will use a seed of 360 unless otherwise specified and will not show this command in the text (though it is shown in the supplements and scripts), but it is used before every script where random numbers are generated. Have fun and set seeds using numbers you enjoy!
The reason that setting seeds is important is that this makes the work reproducible. Reproducibility means that others can take the code and obtain the same results, lending credibility to the work. While writing simulations, you should aim to make sure all your code is reproducible.
Example 1.33 The script Divisible356.R simulates the divisibility problem in Example 1.30that a random integer from is divisible by 3, 5, or 6. The problem, and the resulting code, is more complex.The function simdivis() simulates one trial. Inside the function, the expression num%%x==0 checks whether num is divisible by . The if statement checks whether num is divisible by 3, 5, or 6, returning 1 if it is, and 0, otherwise.After defining the function, typing simdivis() will simulate one trial. By repeatedly typing simdivis() on your computer, you get a feel for how this random experiment behaves over repeated trials.In this script, instead of writing a loop, we use the replicate command. This powerful R command is an alternative to writing loops for simple expressions. The syntax is replicate(n,expr) . The expression expr is repeated times creating an -element vector. Thus, the result of typing> simlist <- replicate(1000, simdivis())is a vector of 1000 ones and zeros stored in the variable simlist corresponding to success or failure in the divisibility experiment. The average mean(simlist) gives the simulated probability.Play with this script. Based on 1000 trials, you might guess that the true probability is between 0.45 and 0.49. Increase the number of trials to 10,000 and the estimates are roughly between 0.46 and 0.48. At 100,000, the estimates become even more precise between 0.465 and 0.468.We can actually quantify this increase in precision in Monte Carlo simulation as gets large. But that is a topic that will have to wait until Chapter 11.
R: SIMULATING THE DIVISIBILITY PROBABILITY
# Divisible356.R # simdivis() simulates one trial > simdivis <- function() { num <- sample(1:1000,1) if (num%%3==0 || num%%5==0 || num%%6==0) 1 else 0 } > simlist <- replicate(10000, simdivis()) mean(simlist) [1] 0.4707
In this chapter, the first principles of probability were introduced: from random experiment and sample space to the properties of probability functions. We start with discrete sample spaces—sets are either finite or countably infinite. The simplest probability model is when outcomes in a finite sample space are equally likely. In that case, probability reduces to “counting.” Counting principles are presented for both permutations and combinations. Binomial coefficients count: (i) the number of 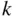 -element subsets of an
-element subsets of an 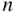 -element set and (ii) the number of
-element set and (ii) the number of 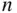 -element binary sequences with a
-element binary sequences with a 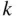 ones. General properties of probabilities are derived from the three defining properties of a probability function. The chapter ends with problem-solving strategies and a first look at simulation.
ones. General properties of probabilities are derived from the three defining properties of a probability function. The chapter ends with problem-solving strategies and a first look at simulation.
Random experiment: An activity, process, or experiment in which the outcome is uncertain.
Sample space : Set of all possible outcomes of a random experiment.
Outcome : The elements of a sample space.
Event: A subset of the sample space; a collection of outcomes.
Probability function: A function that assigns numbers to the elements such thatFor events , .
Equally likely outcomes: Probability model for a finite sample space in which all elements have the same probability.
CountingMultiplication principle: If there are ways for one thing to happen, and ways for a second thing to happen, then there are ways for both things to happen.Permutations: A permutation of is an -element ordering of the numbers. There are permutations of an -element set.Binomial coefficient: The binomial coefficient or “ choose ” counts: (i) the number of -element subsets of and (ii) the number of element sequences with exactly ones. Each subset is also referred to as a combination.
Stirling's approximation: For large ,
Sampling: When sampling from a population, sampling with replacement is when objects are returned to the population after they are sampled; sampling without replacement is when objects are not returned to the population after they are sampled.
Properties of probabilities:Simple addition rule: If and are mutually exclusive, that is, disjoint, then Implication: If implies , that is, if , then .Complement: The probability that does not occur .General addition rule: For all events and , .
Monte Carlo simulation is based on the relative frequency interpretation of probability. Given a random experiment and an event is approximately the fraction of times in which occurs in repetitions of the random experiment. A Monte Carlo simulation of is based on three principles:Trials: Simulate the random experiment, typically on a computer using the computer's random numbers.Success: Based on the outcome of each trial, determine whether or not occurs. Save the result.Replication: Repeat the aforementioned steps times. The proportion of successful trials is the simulated estimate of .
Setting seeds for reproducibility is vital when generating random numbers.
Problem-solving strategies:Taking complements: Finding the probability of the complement of an event, might be easier in some cases than finding , the probability of the event. This arises in “at least” problems. For instance, the complement of the event that “at least one of several things occur” is the event that “none of those things occur.” In the former case, the event involves a union. In the latter case, the event involves an intersection.Inclusion–exclusion: This is another method for tackling “at least” problems. For three events, inclusion–exclusion gives equals
EXERCISES
Understanding Sample Spaces and Events
1 1.1 Your friend was sick and unable to make today's class. Explain to your friend, using your own words, the meaning of the terms (i) random experiment, (ii) sample space, and (iii) event.For the following problems 1.2–1.5, identify (i) the random experiment, (ii) the sample space, and (iii) the event of interest.
Читать дальше

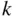 -element subsets of an
-element subsets of an 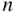 -element set and (ii) the number of
-element set and (ii) the number of 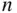 -element binary sequences with a
-element binary sequences with a 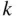 ones. General properties of probabilities are derived from the three defining properties of a probability function. The chapter ends with problem-solving strategies and a first look at simulation.
ones. General properties of probabilities are derived from the three defining properties of a probability function. The chapter ends with problem-solving strategies and a first look at simulation.










