The question was what are the chances that a Canfield solitaire laid out with 52 cards will come out successfully? After spending a lot of time trying to estimate them by pure combinatorial calculations, I wondered whether a more practical method than “abstract thinking” might not be to lay it out say one hundred times and simply observe and count the number of successful plays. This was already possible to envisage with the beginning of the new era of fast computers, and I immediately thought of problems of neutron diffusion and other questions of mathematical physics, and more generally how to change processes described by certain differential equations into an equivalent form interpretable as a succession of random operations. Later [in 1946], I described the idea to John von Neumann, and we began to plan actual calculations.
The Monte Carlo simulation approach is based on the relative frequency model for probabilities. Given a random experiment and some event 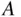 , the probability
, the probability 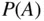 is estimated by repeating the random experiment many times and computing the proportion of times that
is estimated by repeating the random experiment many times and computing the proportion of times that 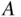 occurs.
occurs.
More formally, define a sequence 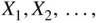 where
where

for 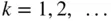 . Then
. Then
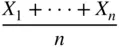
is the proportion of times in which 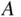 occurs in
occurs in 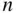 trials. For large
trials. For large 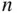 , the Monte Carlo method estimates
, the Monte Carlo method estimates 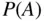 by
by
(1.7) 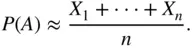
Implementing a Monte Carlo simulation of 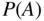 requires three steps:
requires three steps:
1 Simulate a trial: Model, or translate, the random experiment using random numbers on the computer. One iteration of the experiment is called a “trial.”
2 Determine success: Based on the outcome of the trial, determine whether or not the event occurs. If yes, call that a “success.”
3 Replication: Repeat the aforementioned two steps many times. The proportion of successful trials is the simulated estimate of
Monte Carlo simulation is intuitive and matches up with our sense of how probabilities “should” behave. We give a theoretical justification for the method in Chapter 10, where we study limit theorems and the law of large numbers.
Here is a most simple, even trivial, starting example.
Example 1.32 Consider simulating the probability that an ideal fair coin comes up heads. One could do a physical simulation by just flipping a coin many times and taking the proportion of heads to estimate .Using a computer, choose the number of trials (the larger the better) and type the R command> sample(0:1, n, replace = T)The command samples with replacement from times such that outcomes are equally likely. Let 0 represent tails and 1 represent heads. The output is a sequence of ones and zeros corresponding to heads and tails. The average, or mean, of the list is precisely the proportion of ones. To simulate , type> mean(sample(0:1, n, replace = T))Repeat the command several times (use the up arrow key). These give repeated Monte Carlo estimates of the desired probability. Observe the accuracy in the estimate with one million trials:> mean(sample(0:1, 1000000, replace = T)) [1] 0.500376 > mean(sample(0:1, 1000000, replace = T)) [1] 0.499869 > mean(sample(0:1, 1000000, replace = T)) [1] 0.498946 > mean(sample(0:1, 1000000, replace = T)) [1] 0.500115
The Rscript CoinFlip.Rsimulates a familiar probability—the probability of getting three heads in three coin tosses.
R: SIMULATING THE PROBABILITY OF THREE HEADS IN THREE COIN TOSSES
# CoinFlip.R # Trial > trial <- sample(0:1, 3, replace = TRUE) # Success > if (sum(trial) == 3) 1 else 0 # Replication > n <- 10000 # Number of repetitions > simlist <- numeric(n) # Initialize vector > for (i in 1:n) { trial <- sample(0:1, 3, replace = TRUE) success <- if (sum(trial) == 3) 1 else 0 simlist[i] <- success } > mean(simlist) # Proportion of trials with 3 heads [1] 0.1293
The script is divided into three parts to illustrate (i) coding the trial, (ii) determining success, and (iii) implementing the replication.
To simulate three coin flips, use the samplecommand. Again letting 1 represent heads and 0 represent tails, the command
> trial <- sample(0:1, 3, replace = TRUE)
chooses a head or tails three times. The three results are stored as a three-element list (called a vector in R) in the variable trial.
After flipping three coins, the routine must decide whether or not they are all heads. This is done by summing the outcomes. The sum will equal three if and only if all flips are heads. This is checked with the command
> if (sum(trial) == 3) 1 else 0
which returns a 1 for success, and 0, otherwise.
For the actual simulation, the commands are repeated 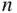 times in a loop. The output from each trial is stored in the vector
times in a loop. The output from each trial is stored in the vector simlist. This vector will consist of 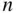 ones and zeros corresponding to success or failure for each trial, where success is flipping three heads.
ones and zeros corresponding to success or failure for each trial, where success is flipping three heads.
Finally, after repeating 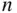 trials, we find the proportion of successes in all the trials, which is the proportion of ones in
trials, we find the proportion of successes in all the trials, which is the proportion of ones in simlist. Given a list of zeros and ones, the average, or mean, of the list is precisely the proportion of ones in the list. The command mean(simlist)finds this average giving the simulated probability of getting three heads.
Run the script via the script file or Rsupplement to see that the resulting estimate is fairly close to the exact solution 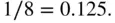 Increase
Increase 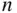 to 100,000 or even a million to get more precise estimates.
to 100,000 or even a million to get more precise estimates. 
Читать дальше

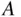 , the probability
, the probability 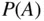 is estimated by repeating the random experiment many times and computing the proportion of times that
is estimated by repeating the random experiment many times and computing the proportion of times that 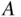 occurs.
occurs.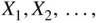 where
where
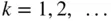 . Then
. Then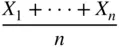
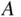 occurs in
occurs in 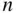 trials. For large
trials. For large 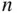 , the Monte Carlo method estimates
, the Monte Carlo method estimates 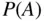 by
by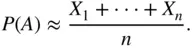
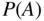 requires three steps:
requires three steps: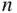 times in a loop. The output from each trial is stored in the vector
times in a loop. The output from each trial is stored in the vector 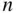 ones and zeros corresponding to success or failure for each trial, where success is flipping three heads.
ones and zeros corresponding to success or failure for each trial, where success is flipping three heads.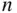 trials, we find the proportion of successes in all the trials, which is the proportion of ones in
trials, we find the proportion of successes in all the trials, which is the proportion of ones in 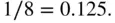 Increase
Increase  to 100,000 or even a million to get more precise estimates.
to 100,000 or even a million to get more precise estimates. 











