Robert P. Dobrow - Probability
Здесь есть возможность читать онлайн «Robert P. Dobrow - Probability» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Probability
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Probability: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Probability»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
distinguished researchers Drs. Robert Dobrow and Amy Wagaman deliver a thorough introduction to the foundations of probability theory. The book includes a host of chapter exercises, examples in R with included code, and well-explained solutions. With new and improved discussions on reproducibility for random numbers and how to set seeds in R, and organizational changes, the new edition will be of use to anyone taking their first probability course within a mathematics, statistics, engineering, or data science program.
New exercises and supplemental materials support more engagement with R, and include new code samples to accompany examples in a variety of chapters and sections that didn’t include them in the first edition.
The new edition also includes for the first time:
A thorough discussion of reproducibility in the context of generating random numbers Revised sections and exercises on conditioning, and a renewed description of specifying PMFs and PDFs Substantial organizational changes to improve the flow of the material Additional descriptions and supplemental examples to the bivariate sections to assist students with a limited understanding of calculus Perfect for upper-level undergraduate students in a first course on probability theory, is also ideal for researchers seeking to learn probability from the ground up or those self-studying probability for the purpose of taking advanced coursework or preparing for actuarial exams.


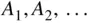 ,
,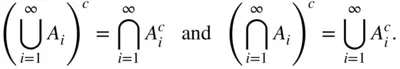
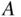 ,
, 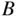 , and
, and 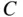 ,
,
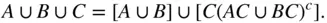
 and
and 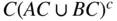 are disjoint. Thus,
are disjoint. Thus,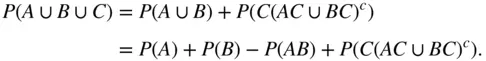
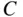 as the disjoint union
as the disjoint union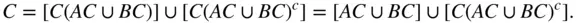
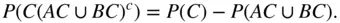
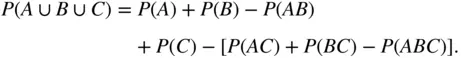
 , the probability that at least one event occurs is
, the probability that at least one event occurs is