John Paul Mueller - Algorithms For Dummies

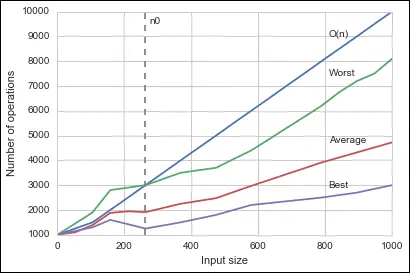
FIGURE 2-1:Complexity of an algorithm in case of best, average, and worst input case.

Many possible functions can result in worse results, but the choice of functions offered by the Big O notation that you can use is restricted because its purpose is to simplify complexity measurement by proposing a standard. This section contains just the few functions that are part of the Big O notation. The following list describes them in growing order of complexity:

Constant complexity O(1): The same time, no matter how much input you provide. In the end, it is a constant number of operations, no matter how long the input data is.

Logarithmic complexity O(log n): The number of operations grows at a slower rate than the input, making the algorithm less efficient with small inputs and more efficient with larger ones. A typical algorithm of this class is the binary search, as described in Chapter 7on arranging and searching data.

Linear complexity O(n): Operations grow with the input in a 1:1 ratio. A typical algorithm is iteration, which is when you scan input once and apply an operation to each element of it. Chapter 4discusses iterations.

Linearithmic complexity O(n log n): Complexity is a mix between logarithmic and linear complexity. It is typical of some smart algorithms used to order data, such as merge sort, heapsort, and quicksort. Chapter 7tells you about most of them.

Quadratic complexity O(n2): Operations grow as a square of the number of inputs. When one iteration is nested inside another iteration, you have quadratic complexity. For instance, you have a list of names and, in order to find the most similar ones, you compare each name against all the other names. Some less efficient ordering algorithms present such complexity: bubble sort, selection sort, and insertion sort.

Cubic complexity O(n3): Operations grow even faster than quadratic complexity because there are multiple nested iterations. When an algorithm has this order of complexity and processes a modest amount of data (100,000 elements) it may run for years. When you have a number of operations that is a power of the input, it is common to refer to the algorithm as running in polynomial time.

Exponential complexity O(2n): The algorithm takes twice the number of previous operations for every new element added. When an algorithm has this complexity, even small problems may take forever. Many algorithms doing exhaustive searches have exponential complexity. However, the classic example for this level of complexity is the calculation of Fibonacci numbers (which, being a recursive algorithm, is dealt with in Chapter 4).

Factorial complexity O(n!): If the input is 100 objects and an operation on a computer takes 10-6 seconds (a reasonable speed for computers today), completing the task will require about 10140 years (an impossible amount of time because the age of the universe is estimated as being 1014 years). A famous factorial complexity problem is the traveling salesman problem, in which a salesman has to find the shortest route for visiting many cities and coming back to the starting city (presented in Chapter 18).

Chapter 3

IN THIS CHAPTER

Considering what Google Colab provides

Using Google Colab to perform common development tasks

Making applications run in Google Colab

Getting help when you need it

Colaboratory ( https://colab.research.google.com/notebooks/welcome.ipynb ), or Colab for short, is a Google cloud-based service that lets you write Python code using a notebook-like environment, rather than the usual IDE. (Jupyter Notebook, https://jupyter.org/ , provides a similar environment to Colab on the desktop if you don’t have an Internet connection.) You don’t have to install anything on your system to use it. The benefit of this approach is that you can work with code in small pieces and obtain nearly instant results from any work you do. A notebook format also lends itself to output in a report format that works well for presentations and reports. The first section of this chapter helps you work through some Colab basics and understand how Colab differs from a standard IDE (and why this difference has a significant benefit when learning algorithms).

You can use Colab to perform specific tasks in a cell-oriented paradigm. The next sections of the chapter go through a range of task-related topics that start with the use of notebooks. Of course, you also want to perform other sorts of tasks, such as creating various cell types and using them to create notebooks that have a report-like appearance with functional code.

Part of working with Colab is knowing how to run the example code, making it run as quickly as possible. Two sections of the chapter are dedicated to using hardware acceleration and running the example code in various ways.

Finally, this chapter can’t address every aspect of Colab, so the final section of the chapter serves as a handy resource for locating the most reliable information about Colab.

You don’t have to type the source code for this chapter manually. In fact, using the downloadable source is a lot easier. You can find the source for this chapter in the \A4D2E\A4D2E; 03; Colab Examples.ipynb file of the downloadable source. See the Introduction for details on how to find these source files.

Colab is designed to mimic a desktop application called Jupyter Notebook ( https://jupyter.org/ ). In fact, it's somewhat difficult to tell the two applications apart in the functionality they provide. Google Colab is the cloud version of Notebook, and the Welcome page makes this fact apparent. It even uses IPython (the previous name for Jupyter) Notebook ( .ipynb) files for the site.

Even though the two applications are similar and they both use .ipynbfiles, they do have some differences that you need to know about. The previous edition of this book used Jupyter Notebook, but Colab offers the ability to compute anywhere on any device that sports a browser, so this edition of the book focuses on Colab instead. The following sections help you understand the Colab differences.

You can use Colab to perform many tasks, but for the purpose of this book, you use it to write and run code, create its associated documentation, and display graphics. The downloadable source for this book is designed to run on Colab, but you can also use it with Jupyter Notebook if you want.

Jupyter Notebook is a localized application in that you use local resources with it. You could potentially use other sources, but doing so could prove inconvenient or impossible in some cases. For example, according to https://docs.github.com/repositories/working-with-files/using-files/working-with-non-code-files , your Notebook files will appear as static HTML pages when you use a GitHub repository ( GitHub is a cloud-based storage technology specifically oriented to working with code.) In fact, some features won't work at all. Colab enables you to fully interact with your Notebook files using GitHub as a repository, and Colab supports a number of other online storage options as well, so you can regard Colab as your online partner in creating Python code.