The weberite structure, Na 2MgAlF 7, is another anion-deficient fluorite superstructure, closely related to pyrochlore that is shown by a range of fluorides and oxides of general formula A 2B 2X 7. The ideal symmetry of weberite is orthorhombic, space group Imma , but several structurally-related polymorphs occur, depending on composition. The anion-deficiency relative to fluorite leads to an overall reduction in cation coordination number with two types of distorted AX 8polyhedra and two sets of BX 6octahedra. It may be regarded as a 3D network of corner-sharing BX 6octahedra, but also as a complex interpenetrating network of corner- and edge-sharing AO 8polyhedra within which the anions occupy three sets of crystallographically-distinct tetrahedral sites. The cations in isolation form ccp layers, equivalent to those in the (111) orientation in fluorite and pyrochlore, but have two stoichiometries, A 3B and AB 3, that alternate. The A components of these layers also form a so-called Kagome network of interlinked hexagons and triangles which may be regarded as cp layers with ¼ of the packing atoms absent.
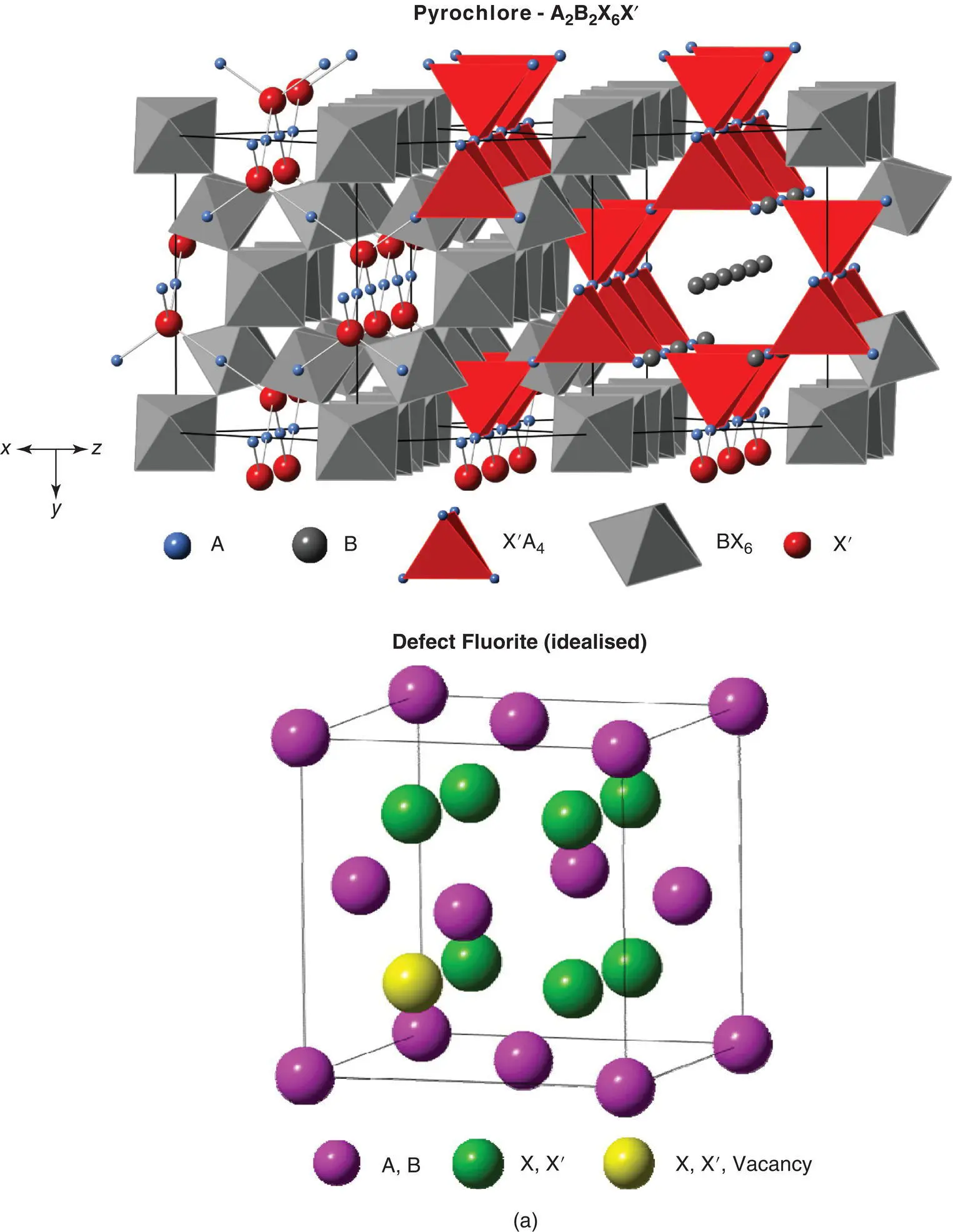
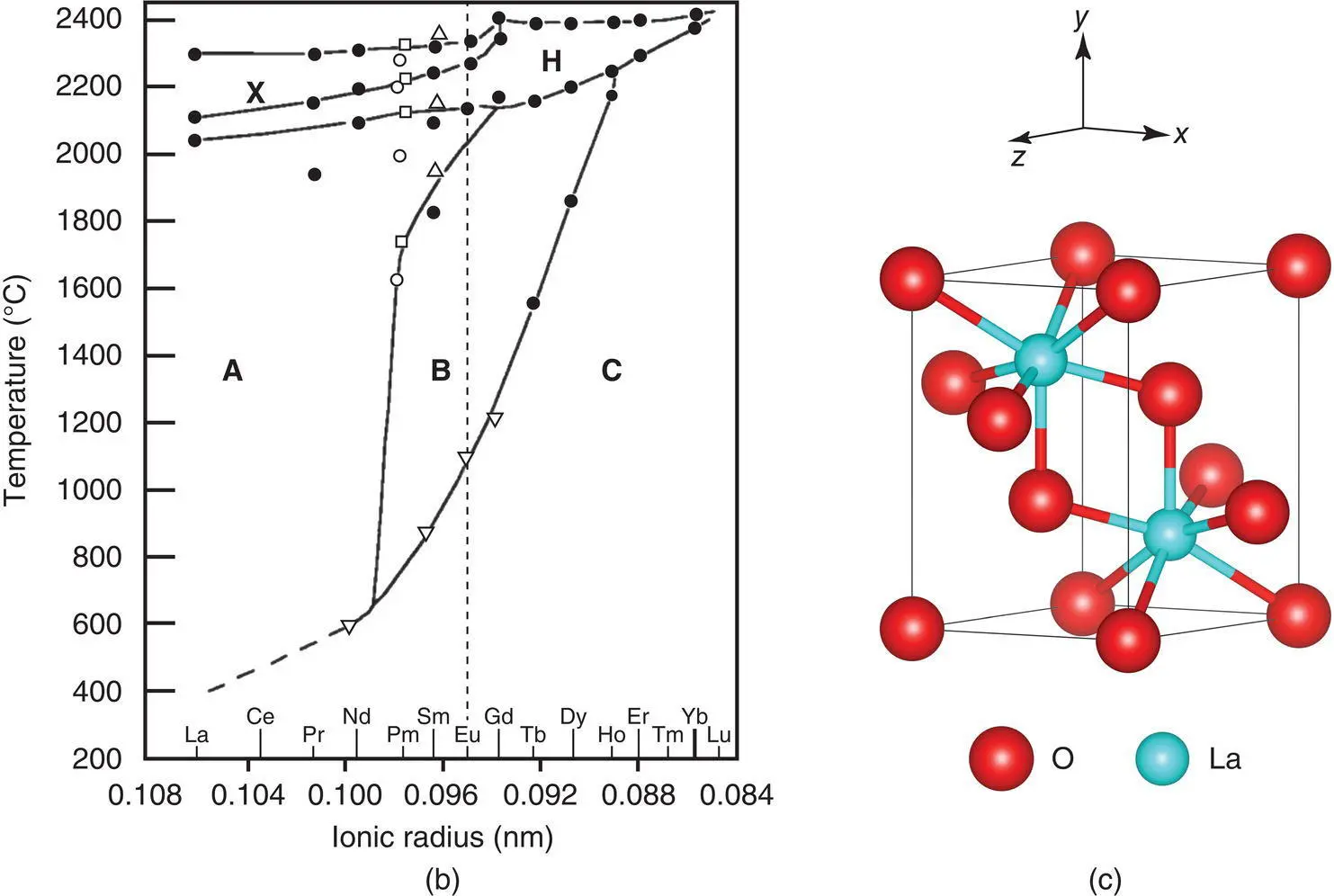
Figure 1.48 The pyrochlore structure, which may be regarded as a distorted, 2 × 2 × 2 superstructure of a cation‐ordered, anion‐deficient fluorite. Anions in eightfold positions, e.g. in fluorite split into two groups in pyrochlore, with one group, X, in 48‐fold positions at e.g. (x, 1/8, 1/8). (b) Temperature‐dependent polymorphism of the rare earth sesquioxides.
G. Adachi and N. Imanaka, Chem. Rev. 98, 1479 (1998).
(c) part of the C-type La2O3 crystal structure showing 7-coordinate La.
A range of complex oxides have weberite structures, in compositional families such as Ln 3NbO 7, better written more informatively as Ln 2(Ln, Nb)O 7: Ln = La, Nd, Gd, Dy; Ln 2B 2O 7: LnB = NdZr, SmTi; A 2Sb 2O 7: A = Ca, Sr, Pb and Ca 2(Ta, Nb) 2O 7(see L Cai and JC Nino, Acta Cryst B 65, 269 (2009) for more details). Weberite oxides are of interest, showing a diverse range of electrical properties. Various weberite fluorides are known, with Na or Ag as the A-cations and different divalent, trivalent B cation combinations such as B 2+: Mg, Mn, Fe, Co, Ni, Cu, Zn and B′ 3+: Sc, V, Cr, Fe, Al, Ga, In, Tl; most interest is in the magnetic interactions associated with the different transition metal combinations in the B sites within the Kagome A sublattice.
The garnets are a large family of complex oxides, including both minerals and synthetic materials, some of which are important ferromagnetic materials; yttrium aluminium garnet (YAG) is used as a synthetic gemstone and when doped with neodymium is the key component in YAG lasers; more recently, garnets with high Li +ion conductivity have been synthesised; garnets have hardness 6.5–7.5 on the Mho scale and are used industrially as an abrasive on sandpaper. They have the general formula A 3B 2X 3O 12: A = Ca, Mg, Fe, etc.; B = Al, Cr, Fe, etc.; X = Si, Ge, As, V, etc. A is a large ion with a radius of ~ 1 Å and has a coordination number of eight in a distorted cubic environment. B and X are smaller ions which occupy octahedral and tetrahedral sites, respectively. Garnets with A = Y or a rare earth: Sm, Gd, Tb, Dy, Ho, Er, Tm, Yb or Lu and B, X = Fe 3+have interesting magnetic properties. One of the most important is yttrium iron garnet (YIG), Y 3Fe 5O 12, the structure of which is shown in Fig. 1.49. Many other A, B, X combinations are possible, such as those in Table 1.25.
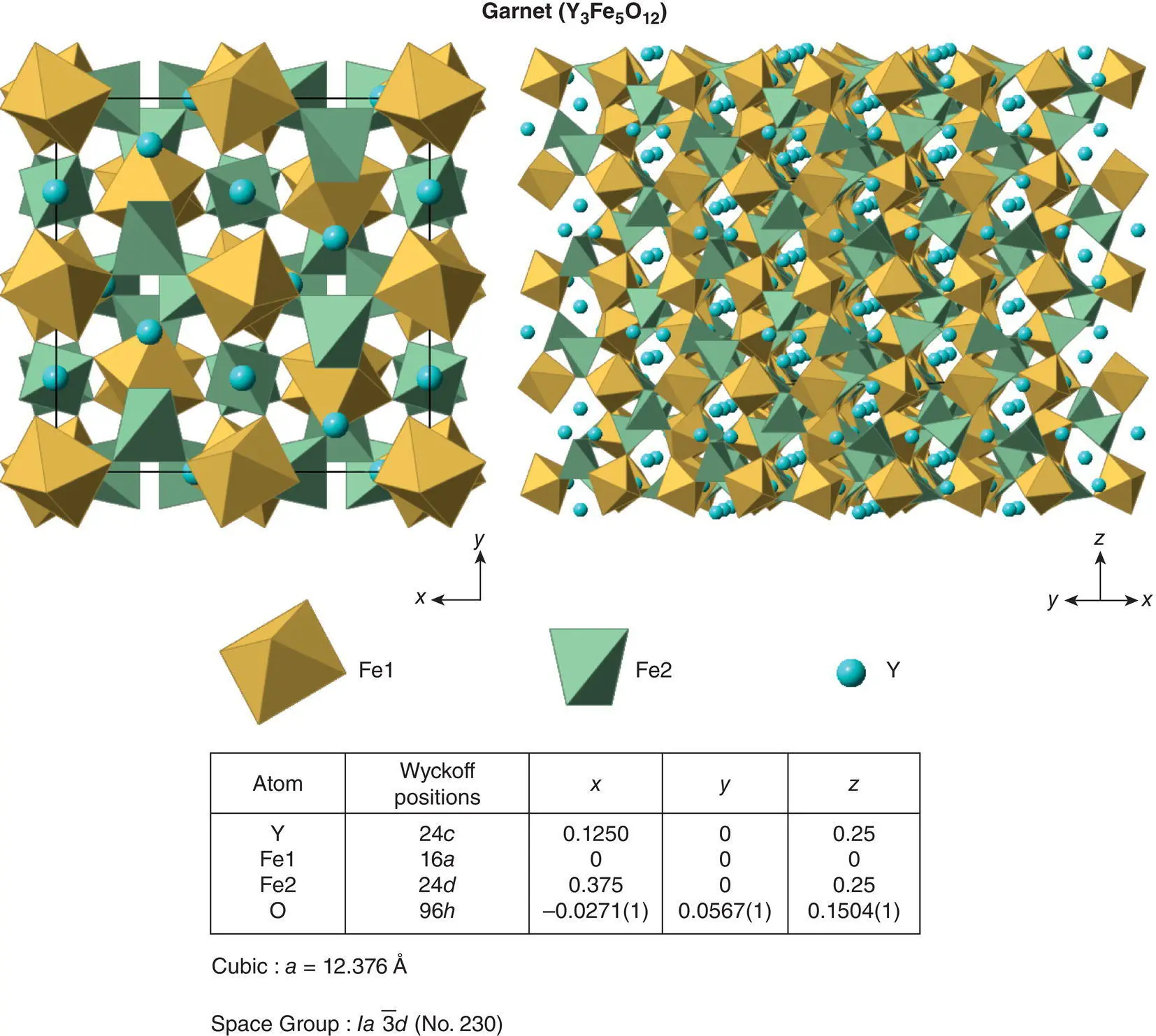
Figure 1.49 The garnet crystal structure.
The unit cell of garnet is body centred cubic, a ≈ 12.4 Å, and contains eight formula units. The structure may be regarded as a framework built of corner‐sharing BO 6octahedra and XO 4tetrahedra. The larger A ions occupy eight‐coordinate cavities within this framework. In YIG and the rare earth garnets, the B and X ions are the same, Fe 3+.
1.17.14 Perovskite‐rock salt intergrowth structures: K 2NiF 4, Ruddlesden–Popper, Aurivillius and Dion Jacobsen phases and layered cuprate superconductors
The K 2NiF 4structure is the simplest structure of a large family of related materials that has attracted much attention in recent years because several of them are superconductors. The structure may be regarded as alternating layers of perovskite and rock salt structures, as shown in Fig. 1.50. The formula K 2NiF 4could be written in expanded form as KNiF 3.KF to indicate the perovskite and rock salt components. The structure is body centred tetragonal with perovskite‐like layers of octahedra centred at c = 0 and 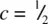 . K +ions lie at the interface between rock salt and perovskite blocks and have a coordination number of 9. The coordination number of K in rock salt would be 12 but the rock salt blocks are less than one unit cell thick and the K coordination in rock salt is interrupted by the atomic displacements that generate perovskite blocks. The K 2NiF 4structure occurs with a range of fluorides and chlorides containing small divalent cations, Table 1.26, and with a range of oxides with different charge combinations such as A 2 +B 6+O 4, A 2 2+B 4+O 4, A 2 3+B 2+O 4, A 2+A′ 3+B 3+O 4and A 2 3+B 1/2+B′ 1/2 3+O 4containing large A and small B cations; probably other cation combinations are also possible.
. K +ions lie at the interface between rock salt and perovskite blocks and have a coordination number of 9. The coordination number of K in rock salt would be 12 but the rock salt blocks are less than one unit cell thick and the K coordination in rock salt is interrupted by the atomic displacements that generate perovskite blocks. The K 2NiF 4structure occurs with a range of fluorides and chlorides containing small divalent cations, Table 1.26, and with a range of oxides with different charge combinations such as A 2 +B 6+O 4, A 2 2+B 4+O 4, A 2 3+B 2+O 4, A 2+A′ 3+B 3+O 4and A 2 3+B 1/2+B′ 1/2 3+O 4containing large A and small B cations; probably other cation combinations are also possible.
Table 1.25 Examples of A, B, X combinations in garnets
| Garnet |
A |
B |
X |
O |
| Grossular |
Ca 3 |
Al 2 |
Si 3 |
O 12 |
| Uvarovite |
Ca 3 |
Cr 2 |
Si 3 |
O 12 |
| Andradite |
Ca 3 |
Fe 2 |
Si 3 |
O 12 |
| Pyrope |
Mg 3 |
Al 2 |
Si 3 |
O 12 |
| Almandine |
Fe 3 |
Al 2 |
Si 3 |
O 12 |
| Spessartine |
Mn 3 |
Al 2 |
Si 3 |
O 12 |
|
Ca 3 |
CaZr |
Ge 3 |
O 12 |
|
Ca 3 |
Te 2 |
Zn 3 |
O 12 |
|
Na 2Ca |
Ti 2 |
Ge 3 |
O 12 |
|
NaCa 2 |
Zn 2 |
V 3 |
O 12 |
A‐site cation ordering occurs in A +A′ 3+B 4+O 4: A = Na, A′ = La → Lu, B = Ti; Na and the lanthanides occupy different layers in the c direction. Anion‐deficient and anion‐excess K 2NiF 4structures exist. For example, in Sr 2XO 3: X = Cu, Pd, one‐quarter of the oxygens are removed, giving square planar coordination for X and seven‐coordinate Sr, whereas in La 2NiO 4+x, interstitial oxygens are present.
The Ruddlesden–Popper series of compounds have the K 2NiF 4structure as their simplest family member; other family members exist with more layers in the perovskite blocks. Thus, with strontium titanates, a family of phases exists with general formula Sr n + 1Ti nO 3n + 1and consist of n SrTiO 3perovskite blocks interleaved with SrO rock salt layers. Two members of this family are Sr 3Ti 2O 7( n = 2) and Sr 4Ti 3O 10( n = 3). The n = ∞ member corresponds to SrTiO 3perovskite. These phases retain a tetragonal unit cell with similar a dimensions but have much longer c axes. A similar family of phases forms for La n + 1Ni nO 3n + 1: n = 1, 2, 3, ∞. In most cases, only one or two members of the Ruddlesden–Popper series are known, with examples such as
Читать дальше




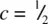 . K +ions lie at the interface between rock salt and perovskite blocks and have a coordination number of 9. The coordination number of K in rock salt would be 12 but the rock salt blocks are less than one unit cell thick and the K coordination in rock salt is interrupted by the atomic displacements that generate perovskite blocks. The K 2NiF 4structure occurs with a range of fluorides and chlorides containing small divalent cations, Table 1.26, and with a range of oxides with different charge combinations such as A 2 +B 6+O 4, A 2 2+B 4+O 4, A 2 3+B 2+O 4, A 2+A′ 3+B 3+O 4and A 2 3+B 1/2+B′ 1/2 3+O 4containing large A and small B cations; probably other cation combinations are also possible.
. K +ions lie at the interface between rock salt and perovskite blocks and have a coordination number of 9. The coordination number of K in rock salt would be 12 but the rock salt blocks are less than one unit cell thick and the K coordination in rock salt is interrupted by the atomic displacements that generate perovskite blocks. The K 2NiF 4structure occurs with a range of fluorides and chlorides containing small divalent cations, Table 1.26, and with a range of oxides with different charge combinations such as A 2 +B 6+O 4, A 2 2+B 4+O 4, A 2 3+B 2+O 4, A 2+A′ 3+B 3+O 4and A 2 3+B 1/2+B′ 1/2 3+O 4containing large A and small B cations; probably other cation combinations are also possible.










