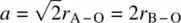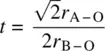Each O has two Ti as its nearest cationic neighbours, at 1.953 Å, and four Sr, coplanar with O at 2.76 Å. However, eight other oxygens are at the same distance, 2.76 Å, as the four Sr. It is debatable whether the O coordination number is best regarded as two (linear) or as six (a grossly squashed octahedron with two short and four long distances) or as 14 (six cations and eight oxygens). No firm recommendation is made!
Having arrived at the unit cell of SrTiO 3, the atomic coordinates, coordination numbers and bond distances, we now wish to view the structure on a rather larger scale and ask the following questions. Does it have cp anions? Is it a framework structure? Answers are as follows.
Perovskite does not contain cp oxide ions as such but O and Sr, considered together, do form a ccp array with the layers parallel to the {111} planes, Fig. 1.41(c) and (e). To see this, compare the perovskite structure with Sr at the origin, (d), with that of NaCl (Fig. 1.2). The latter contains Cl (or Na, depending on the choice of origin) at the corner and face centre positions of the cell and is ccp . By comparison, perovskite contains O at the face centres and Sr at the corner. The structure of the mixed Sr, O cp layers in perovskite is such that one‐quarter of the atoms are Sr, arranged in a regular fashion, Fig. 1.41(e). It is quite common for fairly large cations, such as Sr 2+( r = 1.1 Å), to play apparently different roles in different structures, i.e. as 12‐coordinate packing ions, as in SrTiO 3perovskite, or as octahedrally coordinated cations within a cp oxide array, as in SrO (rock salt structure).
The formal relation between rock salt and perovskite also includes the Na and Ti cations as both occupy octahedral sites: in NaCl, all octahedral sites are occupied (corners and face centres), but in perovskite only one‐quarter [the corner sites in (a)] are occupied. The other octahedral sites at the face centres (c) have oxygen atoms at four corners but Sr at the other two corners and therefore, these sites are rarely occupied in perovskite-related structures.
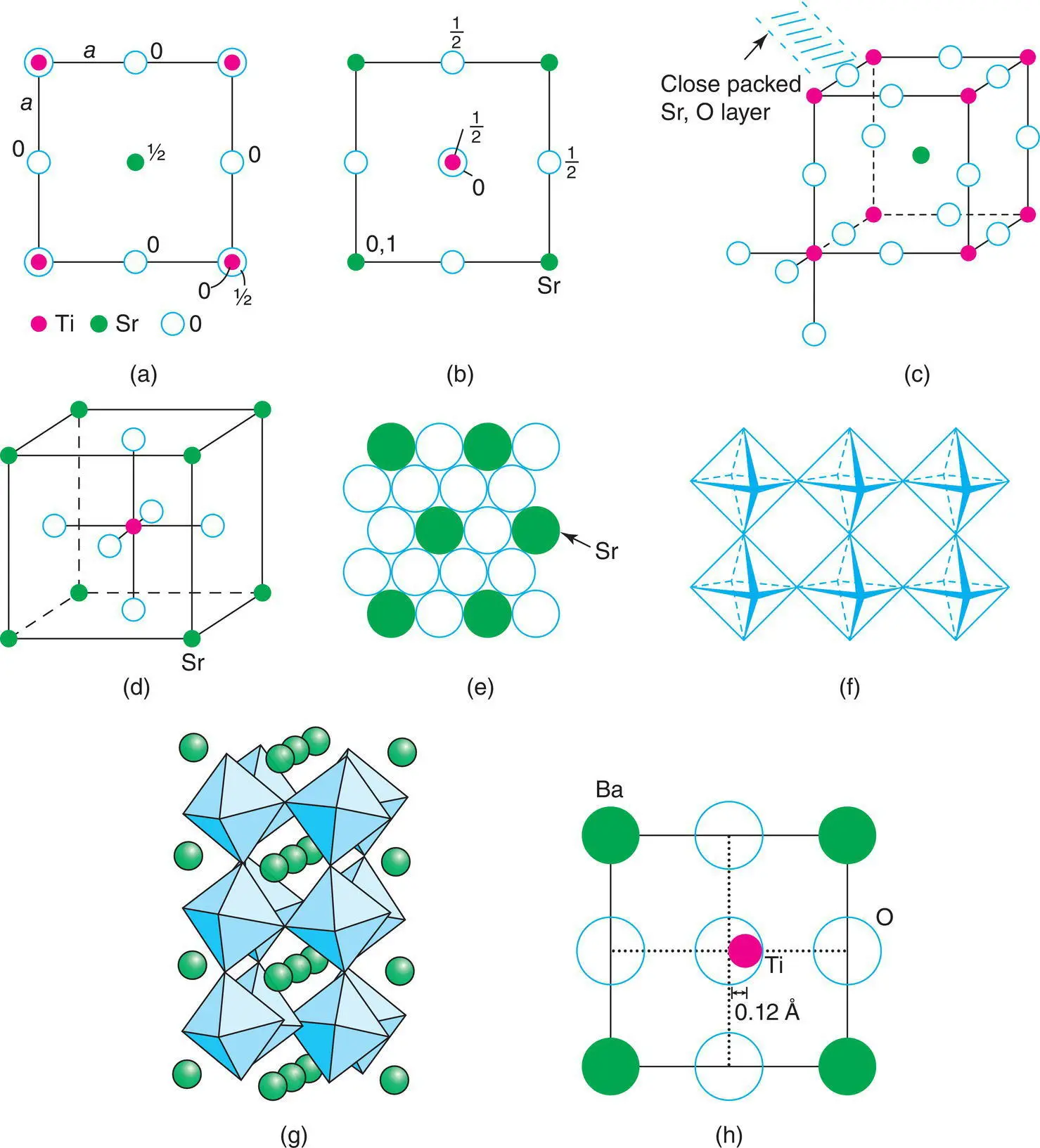
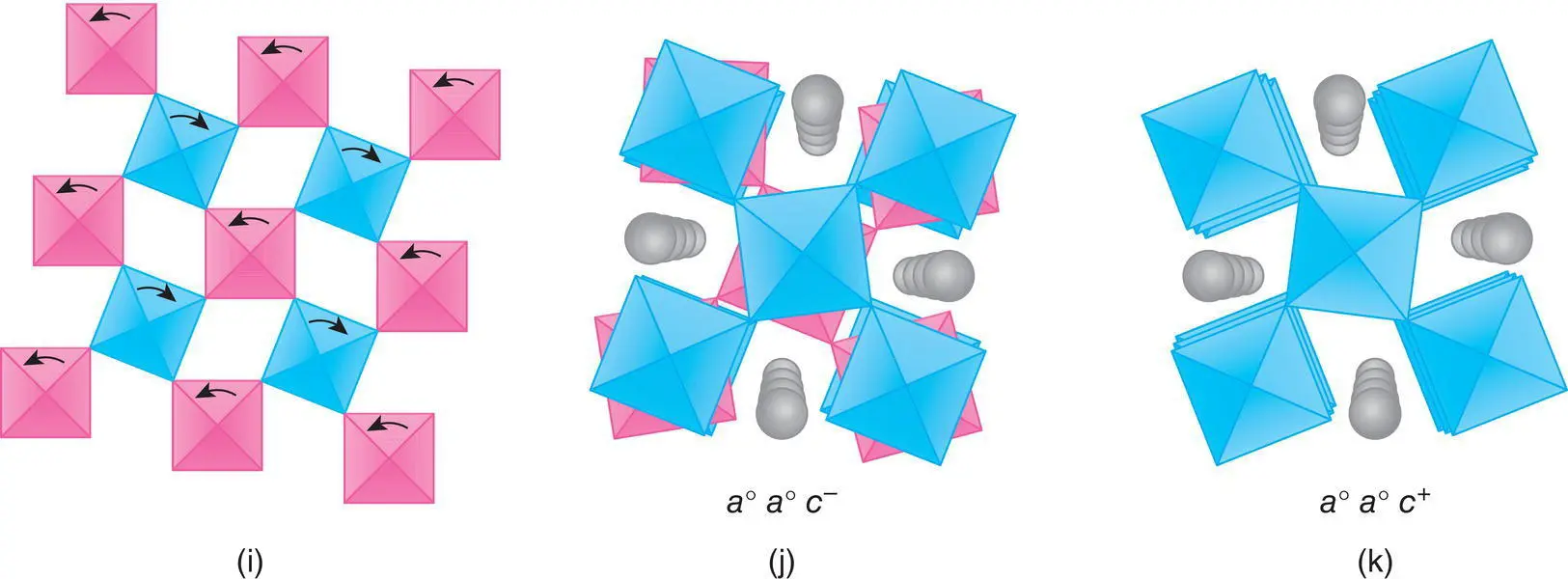
Figure 1.41 (a–d) The perovskite structure of SrTiO3. (e) A close packed Sr, O layer. (f) A layer of corner‐sharing octahedra. (g) GdFeO3 structure. (h) Structure of tetragonal BaTiO3 projected onto the ac plane. Note, the origin of the unit cell is shifted to coincide with Ba rather than with Ti as in (b).
Adapted with permission from M. T. Weller, Inorganic Materials Chemistry, © 1994 Oxford University Press.
(i) Coupled rotation of octahedra in 2D corner‐sharing sheets. (j, k) View looking down the c axis of a0a0c– and a0a0c+ with the A‐site cations shown as spheres and the B‐site cations located at the centre of the octahedra.
Based on M. W. Lufaso and P. M. Woodward, Acta Cryst. Sect. B Struct. Sci. 57, 725 (2001).
Perovskite is also regarded as a framework structure with corner‐sharing TiO 6octahedra and with Sr in 12‐coordinate interstices. The octahedral coordination of one Ti is shown in Fig. 1.41(c) and (d); each O of this octahedron is shared with one other octahedron, such that the Ti–O–Ti arrangement is linear. Thus, octahedra link at their corners to form sheets (f), and neighbouring sheets link similarly to form a 3D framework.
Several hundred oxides and halides form the perovskite structure; a selection is given in Table 1.18. The oxides contain two cations whose combined oxidation state is six. Thus, possible combinations are +I, +V as in KNbO 3, +II, +IV as in CaTiO 3and +III, +III as in LaGaO 3. The 12‐coordinate A site cations are, of course, much larger than the six‐coordinate B site cations.
As well as the cubic perovskite structure, described so far, a variety of distorted, non‐cubic structures exist. These lower‐symmetry structures often form on cooling the high‐temperature cubic structure and the framework of octahedra may be slightly twisted or distorted. An example is shown in Fig. 1.41(g) for the structure of GdFeO 3. The reasons for the structural distortions are associated with the size requirements of the 12‐coordinate A and six‐coordinate B sites and whether adjustments to the structure are required to accommodate different‐sized cations. Also, more complex perovskite structures form in which two different cations may occupy either the A or B sites, giving a range of cation ordering possibilities.
1.17.7.1 Tolerance factor
The reason why structural distortions occur in many perovskites is that the A and/or B atoms are not exactly the right size to fit the sites generated by the remainder of the structure. In an oxide with the ideal, cubic perovskite structure, the bond lengths are related to the unit cell dimension, a, by
(1.6) 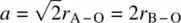
Since bond lengths for each element, oxidation state and coordination number usually fall within closely defined ranges ( Appendix F), it is possible to use equation (1.6)to see how well the sizes of a particular A, B combination meet the requirements for an undistorted, ideal perovskite. The degree to which the sizes depart from equation (1.6)is given by a tolerance factor, t:
Table 1.18 Some compounds with the perovskite structure
| Compound |
a /Å |
Compound |
a /Å |
Compound |
a /Å |
| KNbO 3 |
4.007 |
LaFeO 3 |
3.920 |
|
|
| KTaO 3 |
3.9885 |
LaGaO 3 |
3.875 |
CsCaF 3 |
4.522 |
| KIO 3 |
4.410 |
LaVO 3 |
3.99 |
CsCdBr 3 |
5.33 |
| NaNbO 3 |
3.915 |
SrTiO 3 |
3.9051 |
CsCdCl 3 |
5.20 |
| NaWO 3 |
3.8622 |
SrZrO 3 |
4.101 |
CsHgBr 3 |
5.77 |
| LaCoO 3 |
3.824 |
SrHfO 3 |
4.069 |
CsHgCl 3 |
5.44 |
| LaCrO 3 |
3.874 |
SrSnO 3 |
4.0334 |
|
|
(1.7) 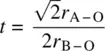
In practice, there is some flexibility over bond lengths and usually, a cubic perovskite forms with t in the range 0.9 < t < 1.0.
For t > 1, the B site is larger than required. If t is only slightly greater than 1.0, the structure distorts but is still basically a perovskite as in BaTiO 3, t = 1.06. There may also be a change in the stacking sequence of the AX 3close packed layers from ccp to hcp to give the family of hexagonal perovskites typified by BaNiO 3. For larger departures from t = 1.0, however, the B ion demands a smaller site, of lower coordination number, and the structure changes completely, as in BaSiO 3which has tetrahedral Si.
For smaller tolerance factors, 0.85 < t < 0.90, several different kinds of structural distortion occur because now, as in GdFeO 3, the A cation is too small for its site. These distortions generally involve tilting and rotation of the BO 6octahedra as shown in Fig. 1.41(g). Consequently some, or all, of the B–O–B linkages are no longer linear but are zig‐zag, which has the effect of reducing the size of the A cation site.
Читать дальше