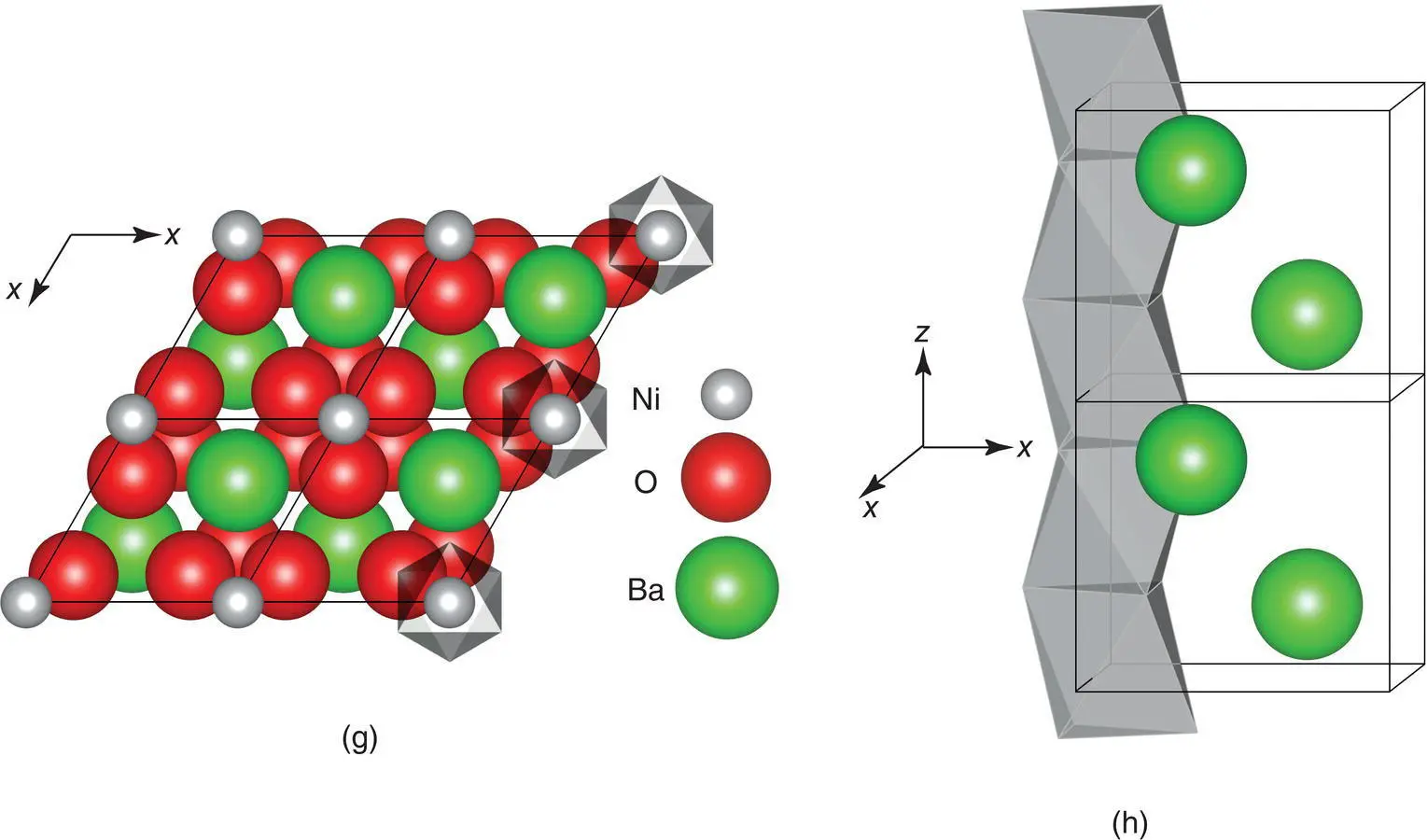
BaTiO 3is tetragonal at room temperature, a = 3.995, c = 4.034 Å, with the structure shown in projection on the ac plane in Fig. 1.41(h). Since Ti is slightly too small for its octahedral site, it displaces by about 6% of the Ti–O distance towards one of the corner oxygens; Ba 2+ions also undergo a smaller displacement in the same direction. This reduces the coordination of Ti to five (square pyramidal) and, to have reasonable Ti–O bond lengths, the structure also contracts slightly in the ab plane [not shown in (h)].
Ti atoms in adjacent unit cells undergo a similar displacement in the same direction and the resulting structure has a large dipole moment due to the separation of positive and negative charge centres. It is possible to flip the orientation of the dipoles: under the action of an applied electric field, the Ti atoms move through the centre of the octahedral site towards one of the other corner oxygens. This ready reversibility gives the structure high polarisability and a high permittivity (or dielectric constant) and is responsible for the property of ferroelectricity (see Section 8.7).
1.17.7.3 Tilted perovskites: Glazer notation
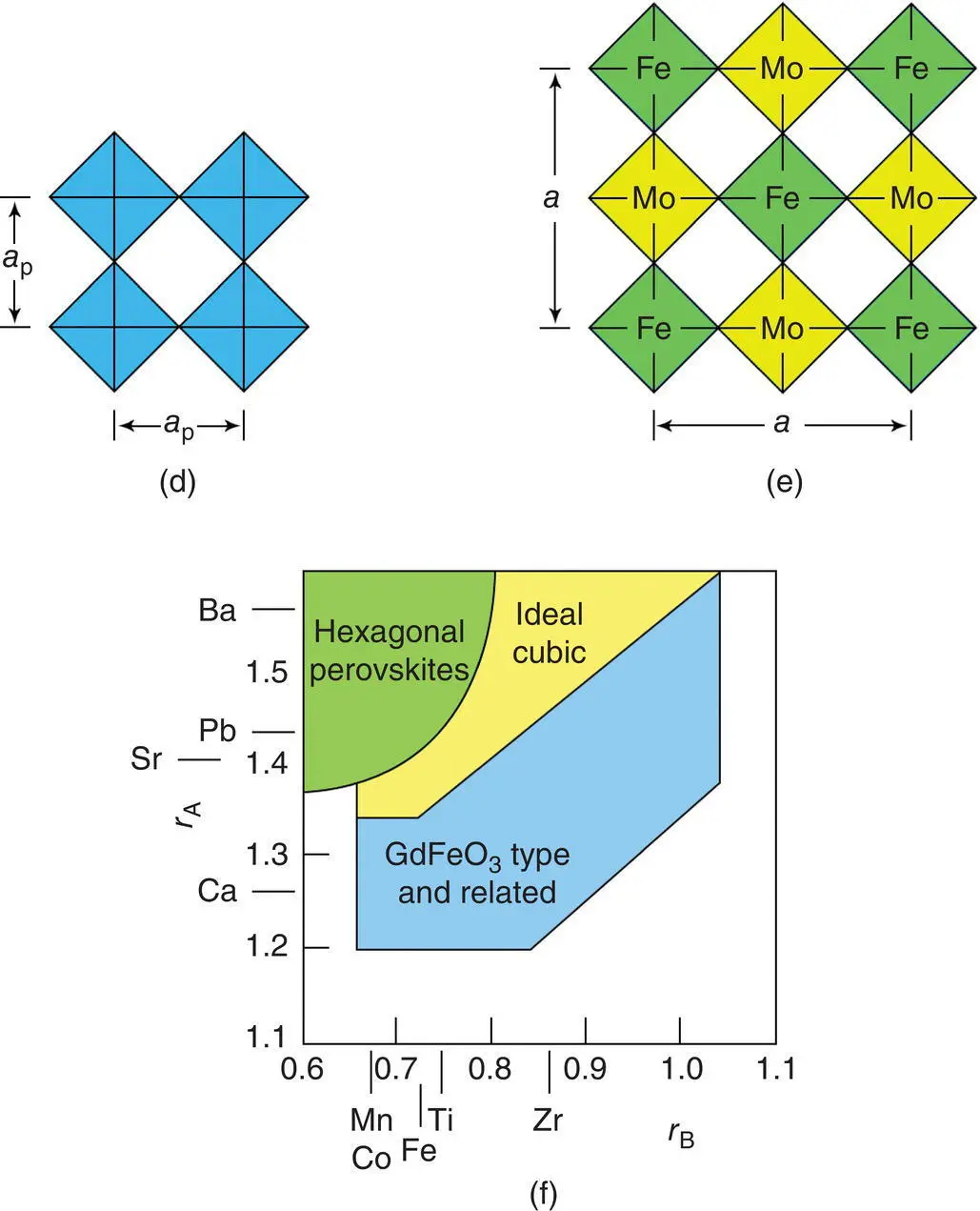
We saw in Fig. 1.41(g) how octahedra can tilt or rotate cooperatively leaving the BO 6octahedra essentially unchanged but reducing the size of the A site and its coordination number. Thus, in GdFeO 3, the A site is eight‐coordinate instead of 12‐coordinate. Such structural distortions occur when the A cation is too small to occupy comfortably the 12 coordinate sites created by the array of corner‐sharing BO 6octahedra and, consequently, the octahedral rotations allow a reduction in the A–O bond length.
A wide variety of structural distortions occur in perovskites whose tolerance factor is less than unity. The most common distortion involves tilting or rotation of octahedra about one or more of the three axes of the octahedron. This is a cooperative process since octahedra link at their corners to adjacent octahedra in the 3D framework and, for instance, clockwise rotation of an octahedron about one axis causes anticlockwise rotation of the adjacent octahedra, Fig. 1.41(i). For the example shown, octahedra which form sheets in the xy plane undergo coupled rotations about the z axis.
Similar coupled rotations may or may not also occur about x and y axes. Within a given sheet of octahedra, the octahedral rotations cannot occur independently of each other since clockwise rotation of one octahedron demands anticlockwise rotation of the four adjacent, corner‐linked octahedra. However, between adjacent planes in, for instance, the z direction there is no automatic coupling between adjacent planes. This gives rise to two commonly observed possibilities in which the octahedral rotations in adjacent planes are identical or the exact opposite.
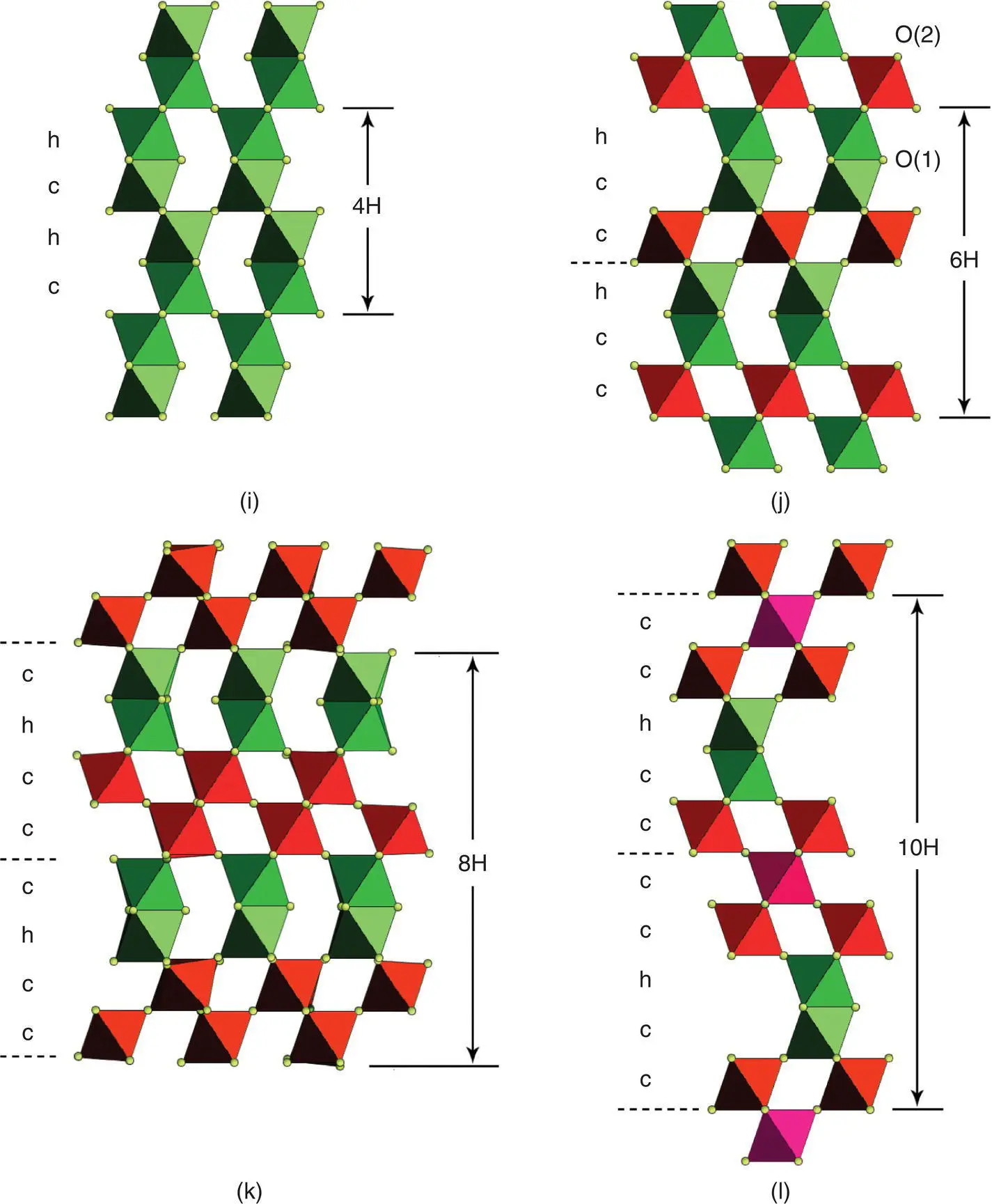
These two possibilities are illustrated in Fig. 1.41(j) and (k). Detailed analysis has shown that 15 different tilt systems are theoretically possible and classification schemes have been developed by Glazer and Alexandrov. The widely used Glazer method is as follows:
1 Starting with the undistorted cubic perovskite, the three axes of the octahedron are given the letters a, b and c. If the degree of any rotation about all three axes is the same, they are labelled. aaa; if rotation about one axis is different, for example about c, the labelling is aac.
2 Each of the three letters carries a superscript; if there is no rotation about that axis, the superscript is 0; if the rotation between adjacent planes of octahedra is the same, and in‐phase, the superscript is +; if the rotation between adjacent planes is in the opposite sense, the superscript is –.
For the examples shown in Fig. 1.41(j) and (k), rotation of octahedra about only one axis is shown and therefore the two possibilities are labelled a 0 a 0 c –and a 0 a 0 c +. These are easy to appreciate since the rotations are about one axis only. For cases involving rotation about all three axes, detailed scrutiny of the structures may be needed; thus for GdFeO 3, the tilt system is a – b + a –although this may not be readily apparent from diagram (g). The different tilt systems give rise to structures with unit cells that are usually no longer cubic. For instance, GdFeO 3has a larger orthorhombic unit cell with 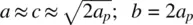 , where a prefers to the parent cubic perovskite cell. Hence the unit cell of GdFeO 3is four times larger than the cubic perovskite cell and contains four formula units. The a – b + a –tilt system is the most commonly observed distorted perovskite structure. Another common tilt system is a – a – a – , which leads to a trigonal unit cell; it is shown by phases such as LaBO 3: B = Co, Ni, Cu, Al, and Ga.
, where a prefers to the parent cubic perovskite cell. Hence the unit cell of GdFeO 3is four times larger than the cubic perovskite cell and contains four formula units. The a – b + a –tilt system is the most commonly observed distorted perovskite structure. Another common tilt system is a – a – a – , which leads to a trigonal unit cell; it is shown by phases such as LaBO 3: B = Co, Ni, Cu, Al, and Ga.
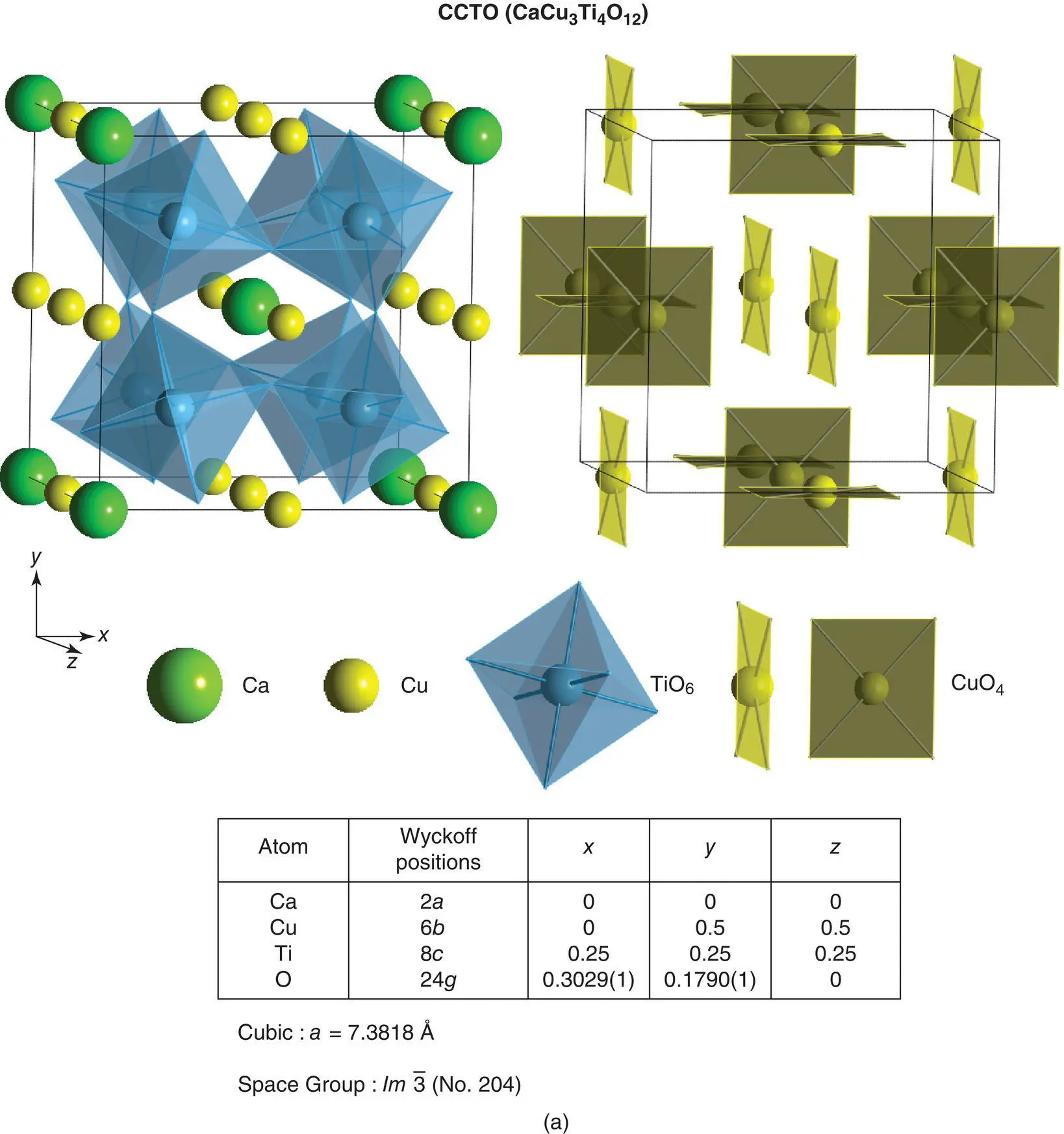
An interesting tilt system which retains cubic symmetry is a + a + a +and is shown by a family of phases with general formula A′A″ 3B 4O 12with CaCu 3Ti 4O 12as the most studied example. The TiO 6octahedra undergo similar coupled rotations about all three axes; a consequence of this is that three‐quarters of the A sites change their coordination from 12‐coordinate to square planar. This structure is shown by a number of compounds in which Cu, Mn and Ni occupy the square planar A″ sites, Fig. 1.42(a) discussed next.
1.17.7.4 CaCu3Ti4O12, CCTO
There is much recent interest in a family of perovskite‐related phases typified by CaCu 3Ti 4O 12because of the possibility that they exhibit a giant dielectric constant. It is now known that the measured high permittivities are not a property of the bulk crystals but are associated with the grain–grain contacts in ceramics. The high permittivity is a consequence of the geometry of the regions responsible since the capacitance of a region is proportional to its area but inversely proportional to its thickness. CCTO has a most unusual crystal structure since the A sites of perovskite contain intermediate‐size Ca cations whose coordination number is reduced to eight by tilting of TiO 6octahedra together with square planar CuO 4units. The crystal structure is shown in Fig. 1.42(a) in which the left‐hand diagram emphasises tilting of the TiO 6octahedra and the right‐hand diagram shows the square planar Cu‐based units which have three equivalent orientations in the cubic unit cell. In Glazer notation, the tilt system for CCTO is a + a + a +.
Читать дальше

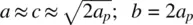 , where a prefers to the parent cubic perovskite cell. Hence the unit cell of GdFeO 3is four times larger than the cubic perovskite cell and contains four formula units. The a – b + a –tilt system is the most commonly observed distorted perovskite structure. Another common tilt system is a – a – a – , which leads to a trigonal unit cell; it is shown by phases such as LaBO 3: B = Co, Ni, Cu, Al, and Ga.
, where a prefers to the parent cubic perovskite cell. Hence the unit cell of GdFeO 3is four times larger than the cubic perovskite cell and contains four formula units. The a – b + a –tilt system is the most commonly observed distorted perovskite structure. Another common tilt system is a – a – a – , which leads to a trigonal unit cell; it is shown by phases such as LaBO 3: B = Co, Ni, Cu, Al, and Ga.
















