Yang Xia - Essential Concepts in MRI
Здесь есть возможность читать онлайн «Yang Xia - Essential Concepts in MRI» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Essential Concepts in MRI
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 100
- 1
- 2
- 3
- 4
- 5
Essential Concepts in MRI: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Essential Concepts in MRI»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
A concise and complete introductory treatment of NMR and MRI Essential Concepts in MRI
Essential Concepts in MRI
Essential Concepts in MRI — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Essential Concepts in MRI», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
Table 2.1lists some fundamental properties of several common nuclei (more lengthy tables can be found in many books and papers [1, 5]). On paper, the bigger γ yields better sensitivity (the column of relative sensitivity, which is defined for the equal numbers of nuclei at constant field.). In practice, one must consider the normal or natural concentration of a nucleus in the specimen (i.e., its availability). For example, the relative sensitivities of 1H and 19F are similar (1 vs. 0.834); however, a human body is about 60% water (~75% in a newborn, 60–65% in men, and 55–60% in women), while the amount of 19F in human or other biological systems is many orders of magnitude smaller by comparison. This explains the challenges and difficulty in detecting the signals other than protons in biological experiments by NMR and MRI.
Table 2.1 Properties of common nuclei.
| Isotope | Abundance (%) | Spin | γ (10 8rad s -1T -1) | Relative sensitivity | Resonance frequency f 0at 1T (MHz) |
|---|---|---|---|---|---|
| 1H | 99.9844 | 1/2 | 2.6752 | 1.00 | 42.577 |
| 2H | 0.0156 | 1 | 0.4107 | 0.00964 | 6.536 |
| 13C | 1.108 | 1/2 | 0.6726 | 0.0159 | 10.705 |
| 19F | 100 | 1/2 | 2.5167 | 0.834 | 40.055 |
| 31P | 100 | 1/2 | 1.0829 | 0.0664 | 17.235 |
2.3 THE TIME EVOLUTION OF NUCLEAR MAGNETIC MOMENT
Now look at the situation when one places a single nucleus in an externally applied magnetic field B 0. Because of the dipole moment, the nucleus (which is represented by a magnetic moment µ) will interact with the external field B 0, from which the energy of the nucleus in the field will be given by a dot product
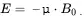 (2.2)
(2.2)
Since the nucleus also has an angular momentum, it experiences a torque, which can be expressed as a cross product, µ× B 0. Since this torque is equal to the time derivative of the angular momentum, by quoting Newton’s second law, we have
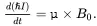 (2.3)
(2.3)
By multiplying the above equation on both sides with γ , we have
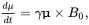 (2.4)
(2.4)
which is shown in Figure 2.3a. In classical mechanics, this equation describes a precessional motion [6] (Figure 2.3b) of µaround B 0at an angular frequency ω0 , known as the Larmor frequency, 1
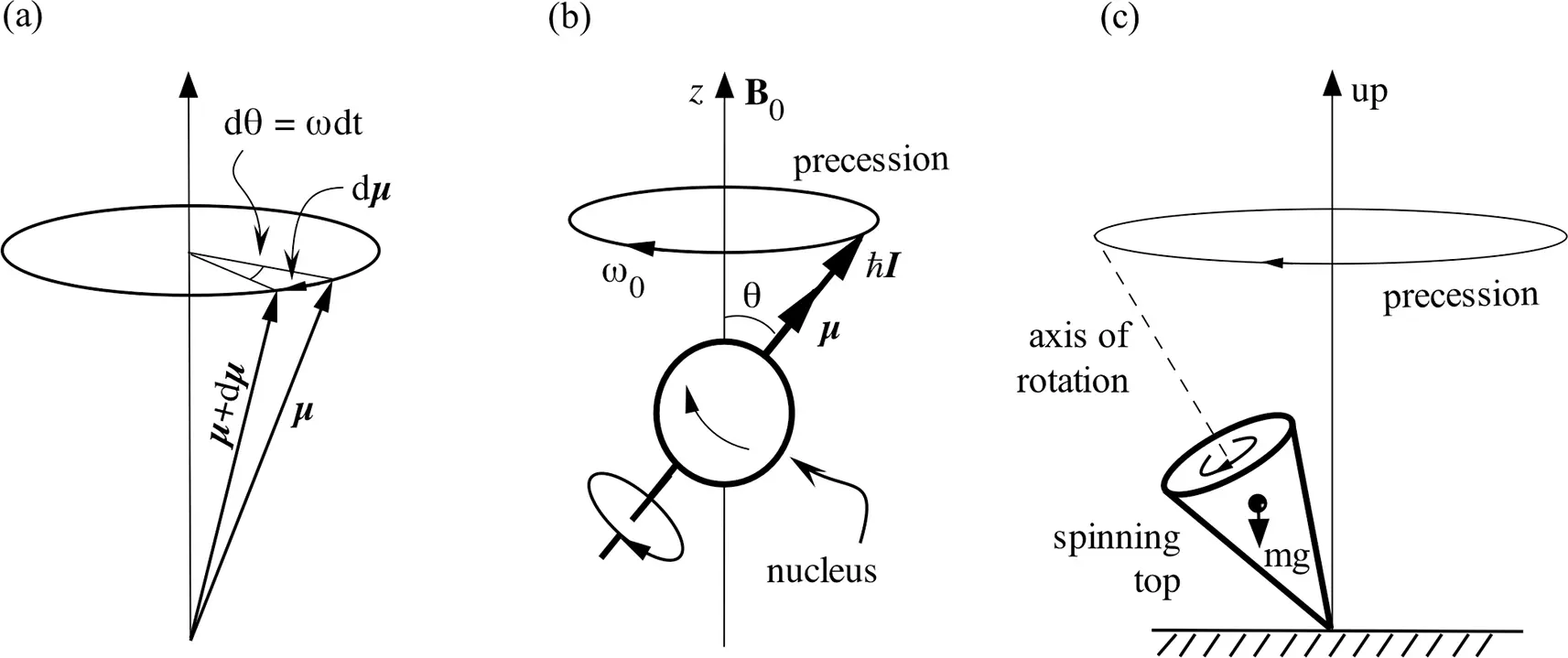
Figure 2.3 (a) Precessional motion in classical mechanics. (b) The Larmor precession of a single nucleus with the aid of classical mechanics. (c) A spinning top can have a precessional motion.
 (2.5)
(2.5)
where ω is expressed as an angular frequency in rad/s, which can be converted to the temporal/linear frequency f in Hz by noting ω = 2πf . Note that when γ is positive (which it is for proton [the nucleus of 1H] and many other nuclei), the rotation will be clockwise, as shown in Figure 2.3b. γ can also be negative (e.g., 3He, 15N), where the rotation becomes counterclockwise.
Although the equation for this Larmor precession seems simple, it is the fundamental equation of the NMR phenomenon. The equation states that (a) the frequency of the nuclear precession is proportional to the externally applied magnetic field B 0, and (b) the proportionality constant is γ . Equation ( 2.4) and Eq. ( 2.5) are useful and accurate for describing the nuclear precession in the presence of an external field B 0.
On a macroscopic scale, one can find several analogs for the precessional motion of the nuclear spin. For example, a spinning top (Figure 2.3c) can have a precessional motion when the axis of rotation does not pass through the top’s center of gravity (i.e., the top is not standing up perfectly vertical), which yields a torque and an angular momentum for the top that induces it into a precessional motion. In a spinning top, the gravitational force mg that points vertically downward plays the same role of the magnetic field B 0 in NMR. Since a top is a macroscopic object, the tipping angle of a spinning top can vary from 0˚ to a large angle continuously, while the tipping angle of a nuclear precessional motion is fixed and cannot be varied. A second common example is the precessional motion of our planet Earth in the solar system, which is tipped at a constant angle of 23.4˚ from an “axis” in space, with a period of the precessional motion of 26,000 years. The torque on Earth is exerted by the sun and the moon.
2.4 MACROSCOPIC MAGNETIZATION
Any practical sample, no matter how small, contains an enormous number of nuclei (remember Avogadro’s constant). The macroscopic (or bulk) magnetization Mis a spatial density of magnetic moments and can be written as
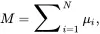 (2.6)
(2.6)
where N is the number of spins in the volume. Since Mis a vector, we can therefore, in general, write Min the component form as
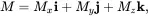 (2.7)
(2.7)
where i, j,and kare the unit vectors along x , y , and z axes, respectively, in the usual 3D Cartesian coordinate system. Equation ( 2.7 )can also be grouped into the transverse and longitudinal forms, as
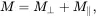 (2.8)
(2.8)
where M ⊥= M x i+ M y j, and M ||= M z k.
In the absence of any external magnetic field, the ensemble average of the nuclear spins in any practical sample should cause the value of magnetization to be averaged to zero, due to the random directions of the magnetic dipoles of the nuclei (since most nuclei act independently).
In the presence of an external field B 0, however, the magnetization Mof a sample with non-zero spin will be non-zero (after the specimen has been immersed in B 0for a sufficient time for the spin system to reach a thermal equilibrium with the environment). This non-zero spin is formed according to Boltzmann’s distribution, which describes the probability distribution function of a particle in an energy state E , as exp(– E/ ( kBT )), where kB is the Boltzmann constant (1.380649 × 10 –23m 2kg s– 2K –1) and T is the absolute temperature of the system. Since the spin-up nucleus is at a lower energy state than a spin-down nucleus, the number of nuclei along the direction of the external magnetic field will be more than the nuclei against the direction of the field (Figure 2.4b). Therefore, a non-zero net magnetization, which can be written in magnitude as M 0, occurs due to the population difference between the spin states at the two spin levels.
Читать дальшеИнтервал:
Закладка:
Похожие книги на «Essential Concepts in MRI»
Представляем Вашему вниманию похожие книги на «Essential Concepts in MRI» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Essential Concepts in MRI» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.












