1 ...7 8 9 11 12 13 ...21 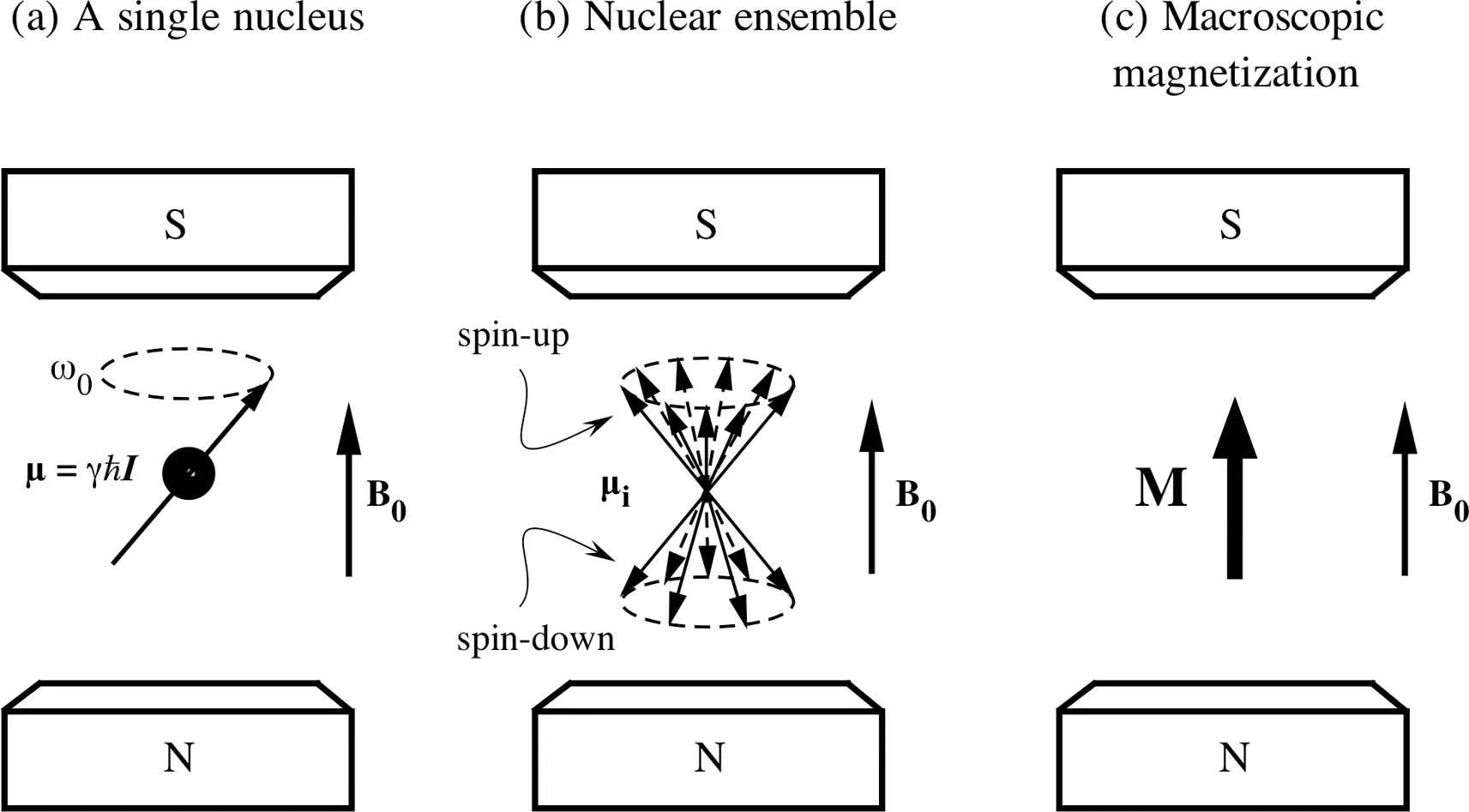
Figure 2.4 (a) A single nucleus in an external magnetic field B 0. (b) A nuclear ensemble that is the collection of a large number of nuclei. (c) The vector average of the nuclear ensemble is represented by a macroscopic magnetization M.
For spin-1/2 particles such as protons, the net magnetization can be visualized as an ordinary vector, aligned in the direction of B 0, as shown in Figure 2.4c. Since any practical sample has an enormous number of nuclear spins, it is easy to see that at thermal equilibrium the net magnetization has no transverse component (i.e., Mx = My = 0); the only component of the net magnetization is along the direction of B 0(i.e., Mz = M 0).
Note that in the classical description, the individual magnetic moment µundergoes precessional motion in an external magnetic field B 0(as in Figure 2.4a), which is commonly represented graphically by vectors on the surface of a cone (as in Figure 2.4b). The ensemble average of µin any practical sample is M, which is represented by a stationary vector that aligns with the direction of B 0(as in Figure 2.4c). At equilibrium, Mitself does not precess graphically as µaround B 0; Mshould be represented by a vector in parallel with B0, never on the surface of any cone.
2.5 ROTATING REFERENCE FRAME
The usefulness of Mis not its equilibrium state but its time evolution after Mis tipped away by an external perturbation (another radio-frequency field) from its thermal equilibrium along the z axis. The evolution of Mproduces the NMR signal, which reveals the environment of the molecules. In a classical description, the time evolution of the macroscopic magnetization in the presence of a magnetic field can follow the same approach that we used before in deriving Eq. ( 2.4 ). By equating the torque to the rate of change of the angular momentum of the macroscopic magnetization M, we have
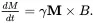 (2.9)
(2.9)
Equation ( 2.9) is a vector equation, which states that the rate of the change of the magnetization has a direction that is at right angles to both the magnetization vector and the magnetic field vector (by the right-hand rule in the cross product of vector analysis, Appendix A1.1). When Bis parallel with the z axis as B 0 k, the above equation has the same solution as given before in Eq. ( 2.5 ), which corresponds to a precessional motion about kat the rate ω 0.
A time evolution of Mcan be introduced by the application of a small linearly polarized radio-frequency (rf) field B 1( t ) that is oscillating in the transverse plane. This B 1field is actually a superposition of two counter-rotating fields in the transverse plane (Figure 2.5):
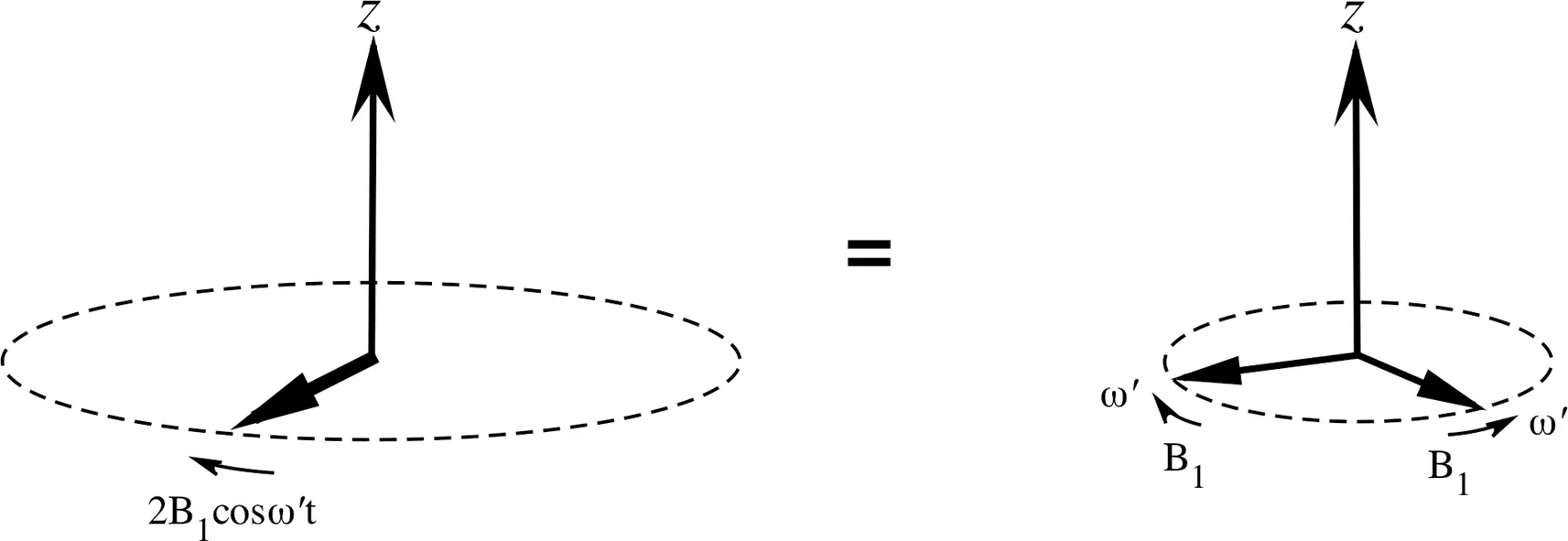
Figure 2.5 Two counter-rotating fields (right) can form a B 1field precessing in the transverse plane of the laboratory reference frame (left).
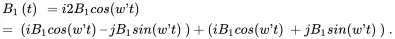 (2.10)
(2.10)
One of the two B 1( t ) components (which rotates in the same direction as ω 0) will have strong influence on the nuclei despite its small magnitude compared with B 0, while the other component, which rotates in the opposite direction, will have negligible effect on the nuclei (provided | B 1| ≪ B 0).
It will be very useful to introduce a rotating frame of reference, as shown in Figure 2.6, where the xyz frame is the laboratory frame of reference (stationary) and the x′ y ′ z ′ frame is the rotating frame of reference at an angular frequency ω′ in the laboratory frame, in which z and z ′ are parallel. In addition, one of the B 1( t ) components appears stationary in the rotating frame; let’s set that stationary component of B 1( t ) along the x ′ axis.
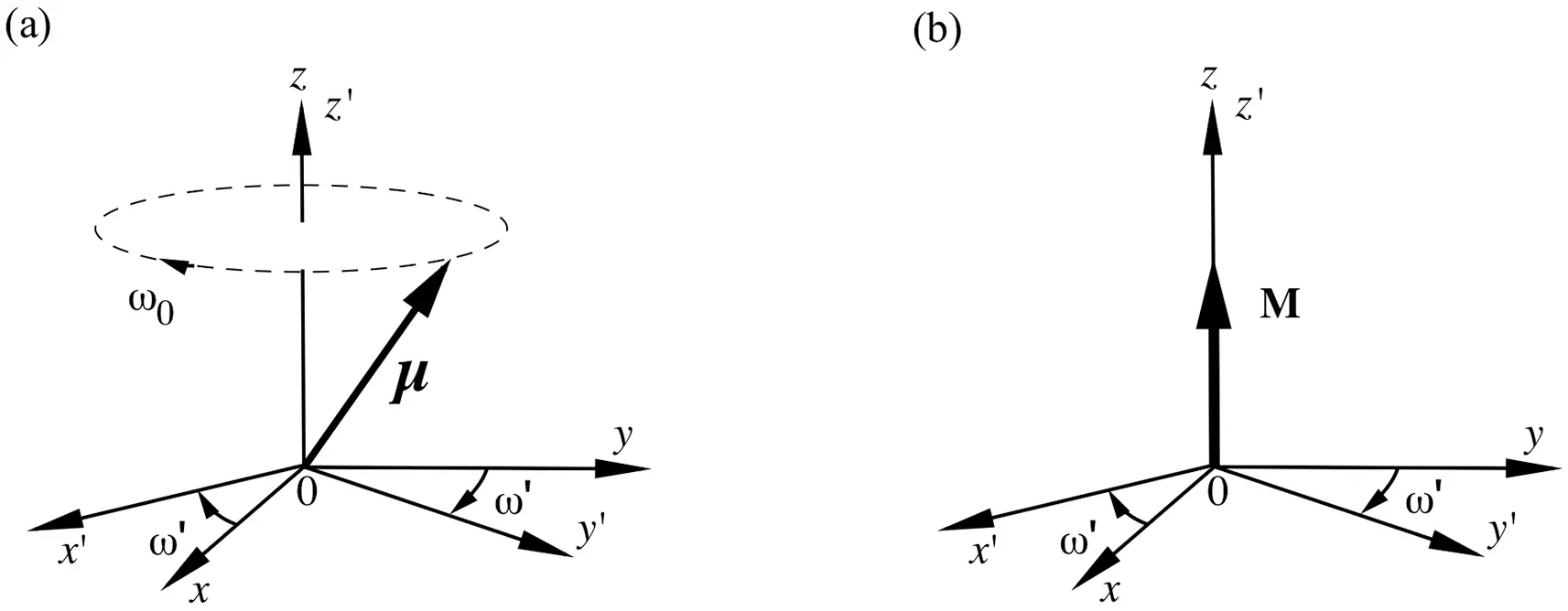
Figure 2.6 (a) A magnetic moment µprecessing in the stationary ( xyz ) and rotating ( x’y’z’ ) frames. (b) A macroscopic magnetization vector Min the two frames.
When a magnetic moment is precessing at a rate of ω 0in the xyz frame, a stationary observer in the x ′ y ′ z ′ frame should see the magnetic moment precessing at a reduced rate ω 0 – ω′ . Since ω = γB , a reduced precession rate implies that the magnetic moment is experiencing a reduced B 0, as
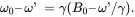 (2.11)
(2.11)
In the presence of both B 0and B 1( t ) fields, the total vector field B totalis the sum of all fields and the effective field B effvaries with the frequency of B 1( t ), as
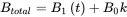 (2.12)
(2.12)
and
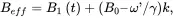 (2.13)
(2.13)
where Eq. ( 2.12 )is for the stationary xyz coordinates and Eq. ( 2.13 )is for the rotating x ′ y ′ z ′ coordinates. The directions of these vector fields are shown schematically in Figure 2.7.
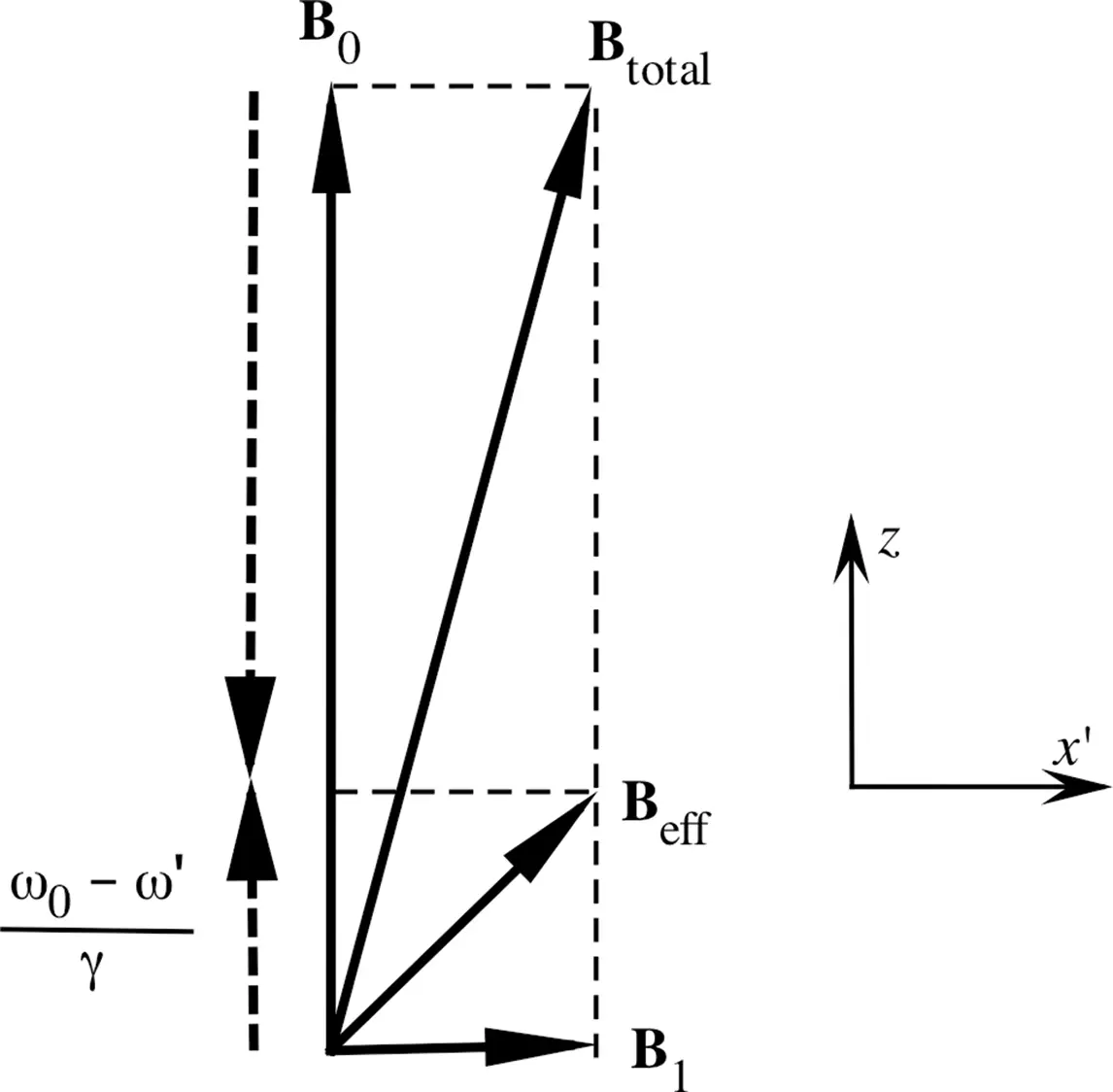
Figure 2.7 In the rotating frame that has a frequency ω′ , the external magnetic field B 0appears to be reduced in magnitude, where the reduction is a function of ω′ . This reduction results in the tipping of B efftowards the x’ axis, which is in parallel with B 1.
In a typical NMR system, | B 1| is several orders of magnitude smaller than B 0, which means that B totalis almost along the z axis. However, the magnitude and the direction of B effwill drastically depend upon the frequency of the rotating frame ω′ . When ω′ approaches the value of ω 0, the effective magnetic field B efftips more towards the transverse plane. When ω′ = ω 0(i.e., the frequency of B 1(t), ω′ , equals the Larmor frequency ω 0), the second term in Eq. ( 2.13 )becomes zero. Hence B 1( t ) becomes the only field in B effto interact with the nuclei. Mwill therefore respond to the effect of B 1( t ), which is set along the x ′ axis (Figure 2.7). This condition, ω′ = ω0 , is termed as the resonance condition.
Читать дальше


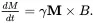 (2.9)
(2.9)
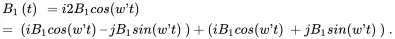 (2.10)
(2.10)
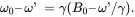 (2.11)
(2.11)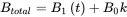 (2.12)
(2.12)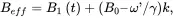 (2.13)
(2.13)











