1 ...8 9 10 12 13 14 ...21 Under this resonance condition, the magnetization will be tipped away from its equilibrium orientation towards the transverse plane under the influence of B 1( t ), as ω 1= γB 1(Figure 2.8). Since the effective component of B 1( t ) has been set along the + x′ axis, the magnetization will rotate about B 1in the y ′ z ′ plane of the rotating frame. Following the notation for rotation as shown in Figure 1.3b, the direction of the magnetization towards the transverse plane under the influence of a B 1field set along the + x′ axis follows the circular trajectory in Figure 2.8b, towards the +y′ axis.
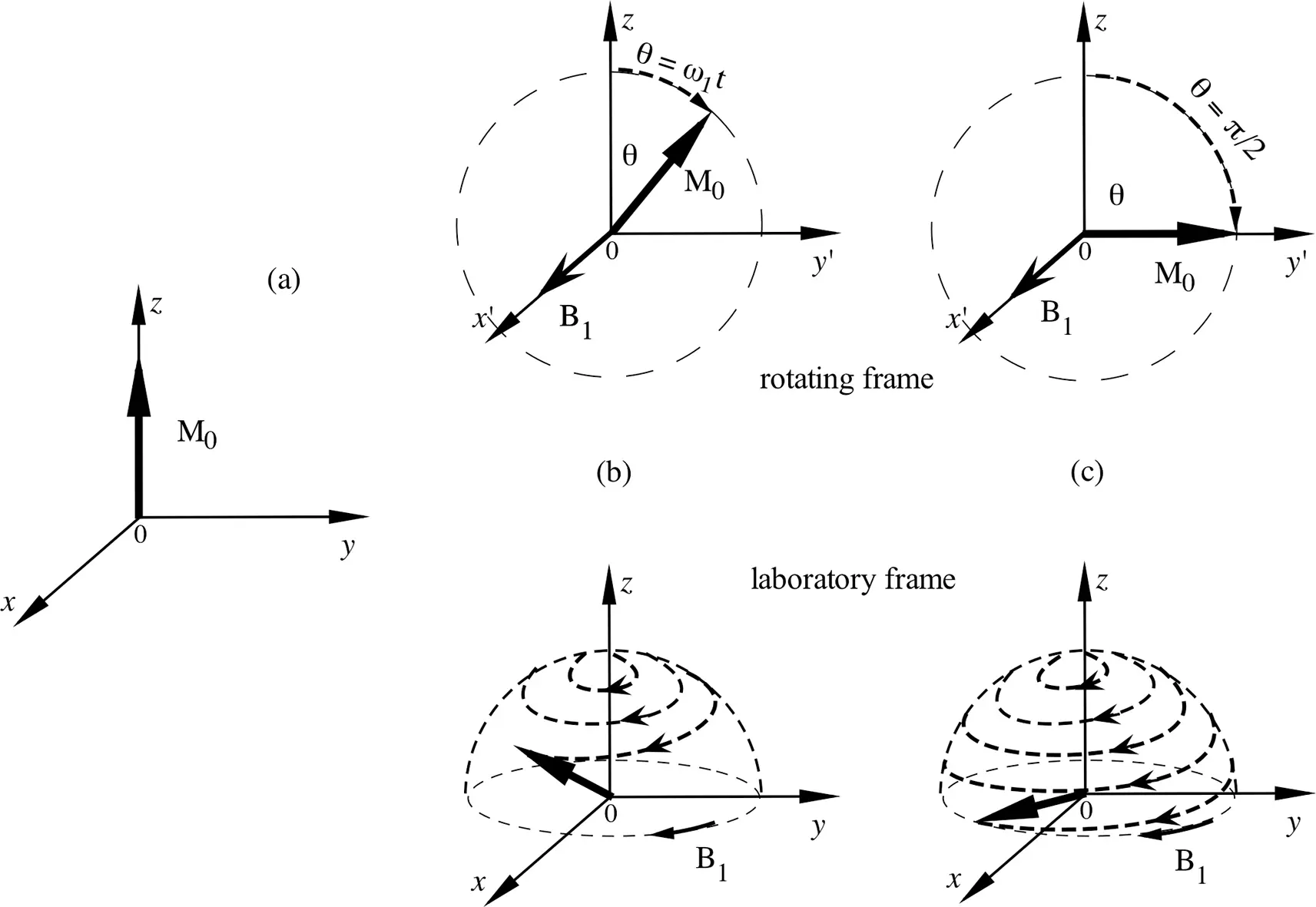
Figure 2.8 Motion of the magnetization in the rotating frame and the laboratory frame, under the influence of a B 1field set along the x’ axis. (a) Mis at the thermal equilibrium, along the z axis. (b) Mtips towards the transverse plane when B 1is turned ON. (c) Mreaches the transverse plane (which is to say that Mhas been rotated by 90˚).
Note that this rotation of the magnetization towards the +y′ axis under a B 1field set at the + x′ axis is determined by the convention of positive rotation that is set earlier in Figure 1.3. As we mentioned in Chapter 1.2, different textbooks and academic papers contain inconsistencies in the notation for rotation of M, to either the –y′ axis or + y′ axis upon a B 1field set along the + x′ axis, depending upon which direction is labeled as the positive rotation. Although this discrepancy seems problematic for the graphical illustration of vectoral motion of magnetization at the first appearance, it does not matter as long as one chooses one notation and keeps it for the entire analysis of spin evolution.
Since B 1is several orders of magnitude smaller than B0 , ω 1is typically tens to hundreds of kilohertz (instead of a typical ω0 at tens to hundreds of megahertz). The time to tip the magnetization from the thermal equilibrium towards the transverse plane is typically several to tens of microseconds (µs), depending upon the magnitude of the B 1field. A particular B 1that is able to tip the magnetization from its z axis to the transverse plane (to the +y′ axis, as shown in Figure 2.8c in the rotating frame x ′ y ′ z′ ) is termed in practice as a 90˚ B 1field (or more commonly a 90˚ B 1pulse, or a π/2 pulse). The term pulse in the last sentence refers to the short duration of the B 1field; see Section 2.10 for the definition of rf pulses and Chapter 7for more description on spin manipulation under various pulse sequences. The motions of the magnetization in the laboratory frame ( xyz ) are also shown in Figure 2.8, which graphically is a spiraling vector away from its equilibrium position over the envelope of a dome. When the magnetization Mreaches the transverse plane, the longitudinal component ( Mz ) of Mbecomes zero.
In general, the equation of motion for Min the presence of B 1( t ) is given by
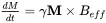 (2.14a)
(2.14a)
or
 (2.14b)
(2.14b)
2.6 SPIN RELAXATION PROCESSES
After Mhas been tipped to the transverse plane, if we switch off the B 1( t ) field and sit there watching, what happens to the spin system? As soon as B 1is switched off, two processes will happen to M, which would eventually lead to the return of Mto thermal equilibrium (i.e., Mz = M 0, and the zero transverse components of M).
The processes that return the magnetization Mto the thermal equilibrium are termed as relaxation, which may be described by two time-constants in the following equations:
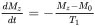 (2.15a)
(2.15a)
and
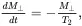 (2.15b)
(2.15b)
where M⊥ refers to the transverse component, defined by Eq. ( 2.8).
T 1is known as the spin-lattice (or longitudinal) relaxation time because the relaxation process involves an energy exchange between the spin system and its surrounding thermal reservoir, known as the “lattice.” The term “longitudinal” comes from the fact that this relaxation process restores the disturbed magnetization to its thermal equilibrium, being along the longitudinal direction k. T 1in simple liquids is usually in the range of several seconds.
When the B 1field rotates the magnetization entirely to the transverse plane (i.e., Mz = 0), the magnetization is said to be rotated by 90˚ (i.e., π/2). The solution to Eq. ( 2.15a) becomes
 (2.16a)
(2.16a)
If the B 1field is sufficiently powerful or its duration is sufficiently long, the magnetization can be inverted (i.e., Mz = – M 0). Such a B 1field is said to rotate the magnetization by 180˚ (a π pulse). Under this condition, the solution to Eq. ( 2.15a) becomes
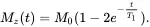 (2.16b)
(2.16b)
Figure 2.9 shows schematically the motion of the longitudinal magnetization with these two different initial conditions, where t = 0 marks the moment that the B 1field is turned off.
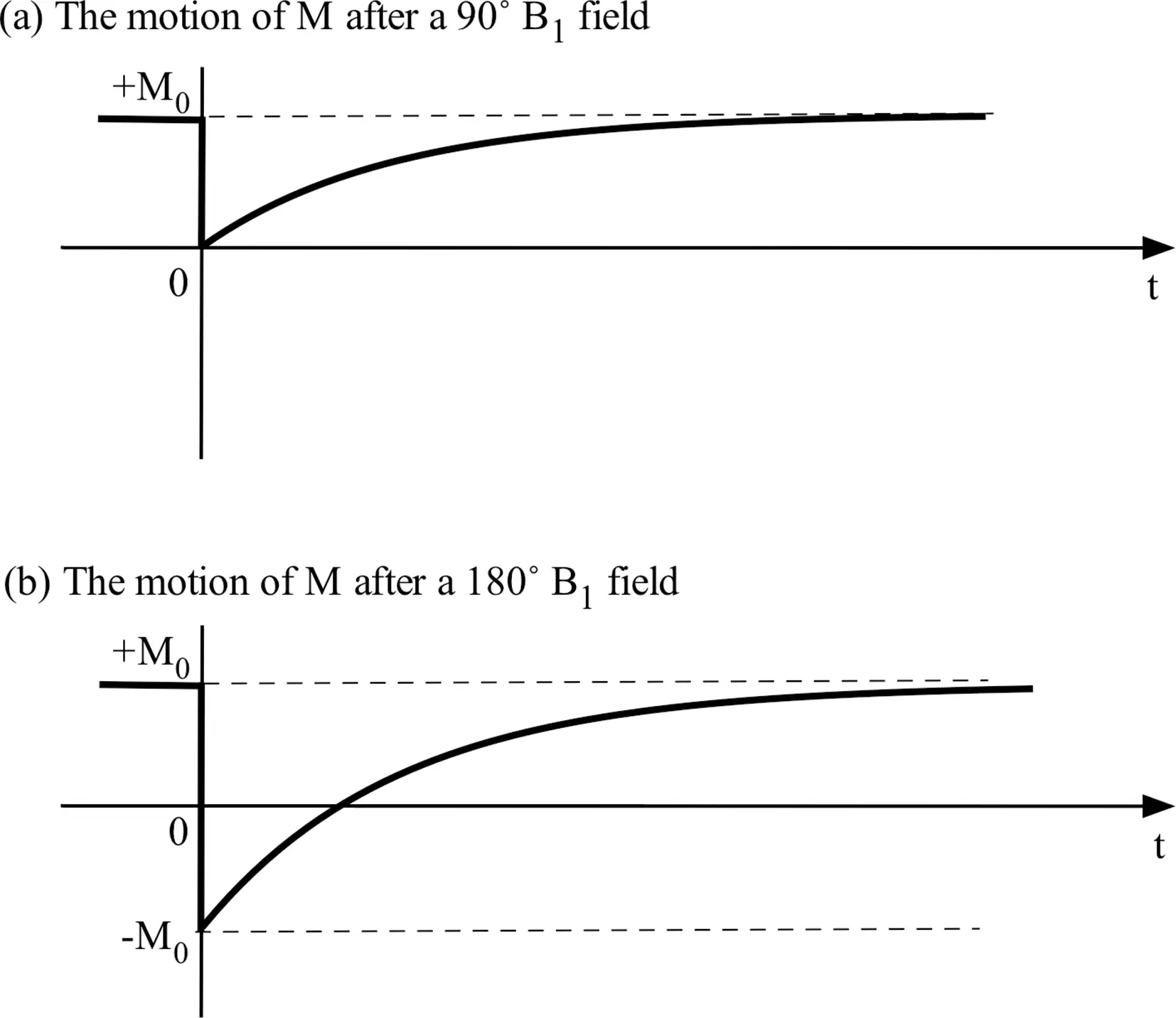
Figure 2.9 The motion of the longitudinal magnetization after it has been tipped by 90˚ (a) and 180˚ (b). The B 1fields that are capable of tipping Mby 90˚ and 180˚ are called a 90˚ B 1field/pulse and a 180˚ B 1field/pulse, respectively.
The second relaxation process is characterized by a time constant T 2, which is called the spin-spin (or transverse) relaxation time since it describes the decay in phase coherence between the individual spins in the transverse plane. This decay in phase coherence describes the process in which the spins come to a thermal equilibrium among themselves in the transverse plane, which results in signal loss since NMR and MRI measure the net transverse magnetization. T 2in biological tissues is usually in the range of tens or hundreds of milliseconds.
The solution to Eq. ( 2.15b) becomes
Читать дальше


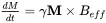 (2.14a)
(2.14a) (2.14b)
(2.14b)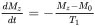 (2.15a)
(2.15a)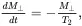 (2.15b)
(2.15b) (2.16a)
(2.16a)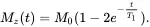 (2.16b)
(2.16b)











