Yang Xia - Essential Concepts in MRI

The simplest and most common nuclei used in NMR and MRI are hydrogen, or protons, a component of the water molecules in the liquid state. Since a proton is a spin-1/2 particle (another quantum mechanical concept) and often very mobile, we could ignore internuclear dipole interactions and scalar coupling between the protons. Hence all states of the nuclear ensemble may be characterized by a vector quantity that is referred to as the nuclear magnetization ( M). The adoption of this vector quantity permits a classical description of magnetic resonance phenomena.

A quantum mechanical description is needed when nuclei experience mutual interactions or have a spin > 1/2 (even if they are independent, due to the presence of the quadrupole interaction). A quantum description is especially important in high-resolution NMR spectroscopy and some advance MRI techniques where the understanding of nuclear interactions is essential.

For the rest of this chapter, the physics of NMR will be described using classical mechanics. Since the classical mechanical description of NMR needs to use a few concepts in quantum mechanics, this type of classical mechanical approach can also be termed as a semi-classical description of NMR.

The theory of electricity and magnetism shows that any motion of a charged body has an associated magnetic field. For example, an electric current is due to the motion of electrons along a conductor on a macroscopic scale. If you bend this conducting wire into a loop, you have just made a coil (Figure 2.1). The coil with an electric current traveling in the wire has an associated magnetic moment, which is the product of the electric current and the area of the coil. When the current-carrying coil is placed in an external magnetic field, the coil will experience a mechanical torque.

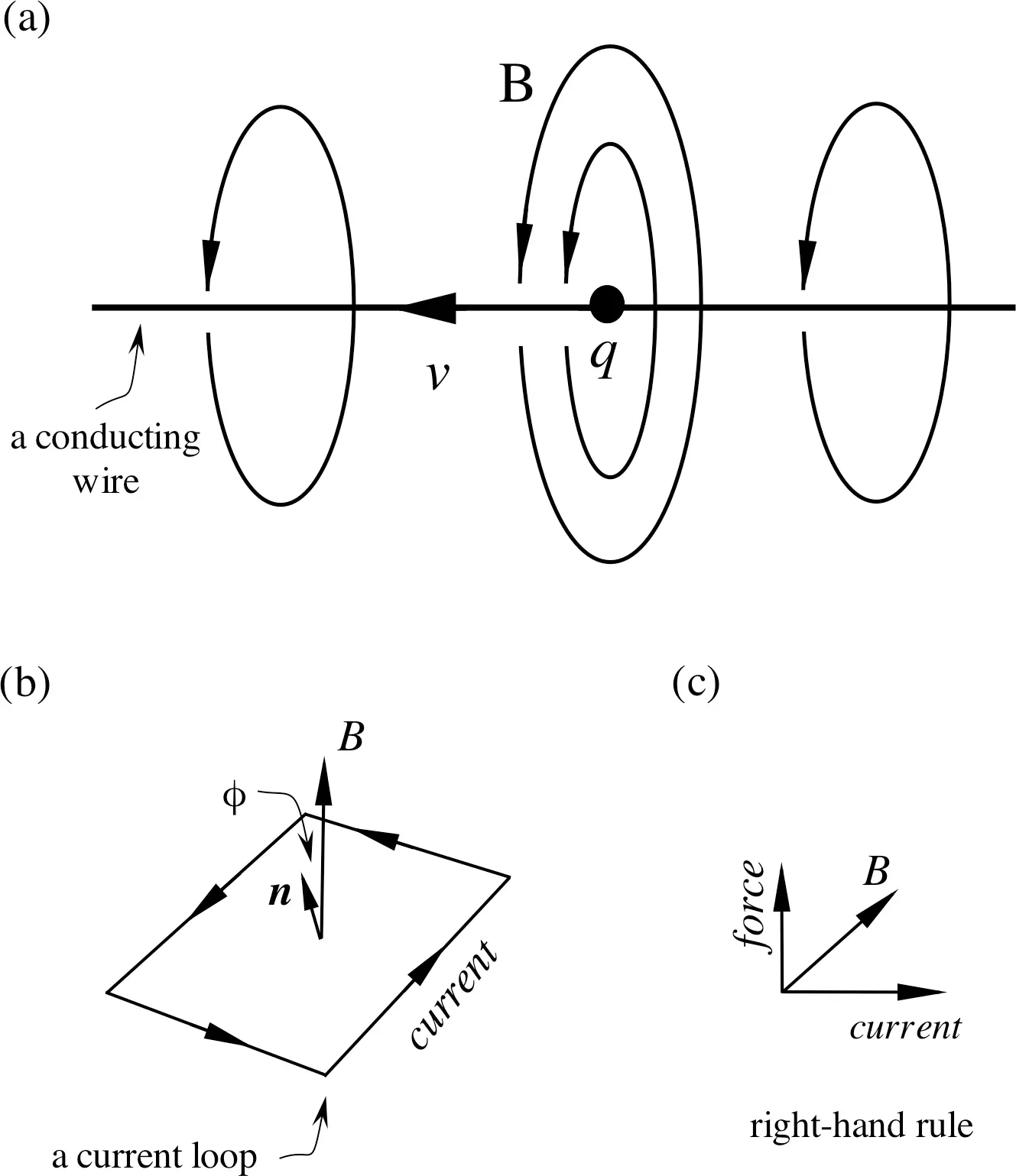
Figure 2.1 (a) Moving charges at velocity v along a conducting wire form an electric current, which has an associated magnetic field Bby the right-hand rule; moving charges carry momentum. (b) An electric current loop has an area and a current. The magnetic moment of the loop µequals to the product of the area and current (which is valid for any shaped loop). nis the normal vector of the current loop; ϕ is the angle between nand B. The torque that causes the rotation of the loop in the magnetic field B is τ= µ× B= (area × current) B sin ϕ . (c) The right-hand rule for the direction of the force on a current-carrying wire in the magnetic field.

This phenomenon can also be extended to the atomic scale: when electrons or nuclei possess angular momentum, there is an associated magnetic moment. Since on the atomic scale, angular momentum is quantized, that is, it can only take certain discrete values (one of the fundamental postulates in modern physics), the magnetic moment is also quantized. (Note that here the angular momentum is a vector quantity since we are using classical mechanics to describe the concept. Later in a quantum mechanical description [ Chapter 3], the angular momentum keeps the same symbol Ibut becomes an operator.)

The angular momentum, labeled as I, is called the spin angular momentum or simply spin, which should be considered as a fundamental property of the nucleus. One could imagine the nucleus as a finite-sized ball spinning on its axis. (Such a spinning ball picture, however, remains valid only in classical mechanics and should be not taken too literally.) The spin Ihas the following properties:

I may have any half-integer or integer value such as 0, 1/2, 1, 3/2, etc. This value is known as the spin quantum number (I).

I will have a fixed value for a given nucleus (due to the even/odd mass and charge number of the nucleus). For example, I = 0 for 12C and 16O; I = 1/2 for 1H (proton), 13C, 19F, 31P; I = 1 for 2H (deuteron) and 14N; and I = 3/2 for 23Na.

If I = 0, then the nucleus has no spin and cannot be observed by NMR (e.g., there is no NMR for 12C, even though each 12C nucleus contains six protons). If I > 0, the nucleus will have an associated magnetic dipole moment µ, given by

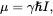(2.1)

where γ is called the gyromagnetic ratio, a characteristic constant for each nuclear species ( γ = 2.675 × 10 8rad s -1T -1or 42.576 MHz T -1for protons), and ħ is the Planck’s constant (6.62607015 × 10 −34J s) divided by 2π. (To convert γ between rad s -1T -1to MHz T -1, consider rad/s as the angular velocity equal to 2π times the linear frequency.) The unit of µis Joule per Tesla (J T -1). Since γ , ħ , and Iare all known constants, the magnitude of µcan be determined accurately.

Note that Eq. ( 2.1) could be also written as γ = µ/( ħ I), which illustrates the fact that γ is the magnetic dipole moment divided by the angular momentum; hence, γ should be more properly named the magnetogyric ratio , not the gyromagnetic ratio that implies the inverse of the two quantities. The term magnetogyric ratio has indeed been used in some books and papers and also recommended by the 2001 International Union of Pure and Applied Chemistry (IUPAC) nomenclature [1]. In modern literature, however, γ is commonly known as the gyromagnetic ratio . Both magnetogyric ratio and gyromagnetic ratio refer to the same value.

The total number of the allowed spin states for a given nucleus is a discrete value, 2 I + 1, which ranges from – I , – I + 1, – I + 2, …, to I . (It is another quantum mechanical concept that we need to cite in the classical description of nuclear magnetic resonance.) These values can be written as mI , the azimuthal quantum number. Hence, a nucleus with

I = 1/2 has two spin states, mI = –1/2 and mI = 1/2. These two spin states are commonly illustrated in quantum mechanics by a two-level energy diagram as in Figure 2.2a, which we will discuss more in Chapter 3. Since there are only two spin states, we may use an arrow to describe the spin-1/2 particles. The mI = –1/2 state is called spin down (↓) while the mI = 1/2 state is called spin up (↑). The spin-down state has higher energy than the spin-up state, hence is the upper level in the energy level diagram (Figure 2.2a). Figure 2.2 The application of an external magnetic field B0 causes (a) a spin-1/2 system to have two discrete energy levels, and (b) a spin-1 system to have three energy levels. Each energy level can be labeled by the individual spin state.

I > 1/2 has nuclear quadrupole moments that produce splitting of the resonant lines or line-broadening effects. For example, a deuteron (2H) has I = 1, which would have three spin states, corresponding to mI = –1, 0, 1. These three spin states can be used to label a three-level energy diagram as in Figure 2.2b. A quantum mechanical description must be used to understand the behavior of any spin with an angular momentum larger than 1/2.

Note that Iis defined in this book as a dimensionless angular momentum; hence, a reduced Planck’s constant has been explicitly included in Eq. ( 2.1). This use of a dimensionless angular momentum can be found in many books, including those by Callaghan [2] and Hennel and Klinowski [3]. In contrast, Ican also be defined as an angular momentum with in its definition [4]. With this definition, Eq. ( 2.1) would be written as µ= γ I.