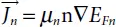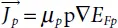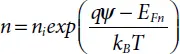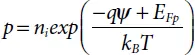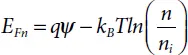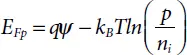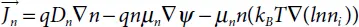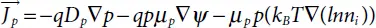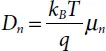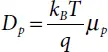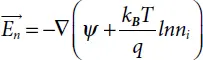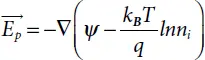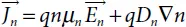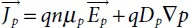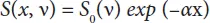The elementary equations for the operation of semiconductor-based devices describe the static and dynamic carrier behavior in semiconductors under external factors, like optical excitation or applied field, both causing deviations from conditions of thermal equilibrium.
The electric potential is related to the density of the space-charge by Poisson equation:
(1.31) 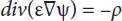
where ψ represents the electrostatic potential, the local permittivity is given by ε , and ρ represents the density of the local space charge.
The total contribution from all charges which may be mobile or fixed, including holes, electrons and ionized impurities is expressed as local space charge density.
(1.32) 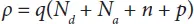
Where the elementary charge is given by q , n gives the electron concentration, p represents the concentration of holes, Na is the concentration of ionized acceptors and Nd is the concentration of ionized donor.
The electric field is obtained by the gradient of the potential as:
(1.33) 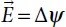
When the electric fields and density gradients are present, the equation of continuity describes the behavior of excess carriers with time and in space:
(1.34) 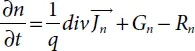
(1.35) 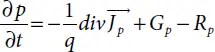
where electron and hole concentrations are represented by n and p respectively. Jn and Jp are the electron current density and hole current density, Gn and Gp are the electrons and hole generation rates, Rn and Rp are the electron and hole recombination rates.
In steady state 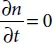 and
and 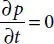 .
.
Current density equations
Derivations focused on the transport theory given by Boltzmann have depicted that the current densities can be approximated in the continuity equations by the drift-diffusion model. In the present case, of the quasi Fermi levels EFn and EFp express the current densities:
(1.36) 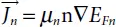
(1.37) 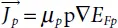
Where μn and μp are the mobilities of the electrons and holes. The quasi-Fermi levels are linked to the carrier concentrations and the potential through the two Boltzmann approximations as follows:
(1.38) 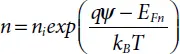
(1.39) 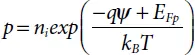
To describe the quasi-Fermi levels these two equations may then be rewritten as:
(1.40) 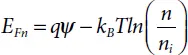
(1.41) 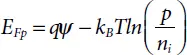
By putting these equations into the expression for current density, the following current relationships can be attained:
(1.42) 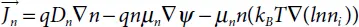
(1.43) 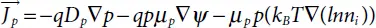
Where Dn and Dp represent the electron and hole diffusion constants, respectively:
(1.44) 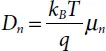
(1.45) 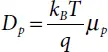
The final term in (1.42)and (1.43)reflects the difference in the effective concentration of the intrinsic carriers, taking into account the decreasing influence of the band-gap. Defining active electrical fields:
(1.46) 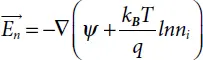
(1.47) 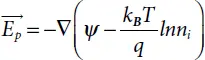
The drift-diffusion equations can then be written in more conventional form as.
(1.48) 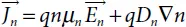
(1.49) 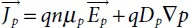
Optical generation of electron-hole pairs
It is necessary to the operation of solar cells to produce electron-hole pairs by absorbing sunlight. Holes and electrons lead to the transition of energy carried by the photons of light into electrical energy.
The number of incident photons S 0(ν) (per unit area, per unit time and per unit energy) determine the number of generated electron-hole pairs. The photon flux S ( x , ν) decreases inside the semiconductor exponentially as:
(1.50) 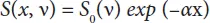
where ν is the frequency. The absorption process in the semiconductor determines the absorption coefficient α (ν).
Читать дальше

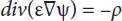
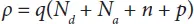
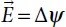
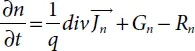
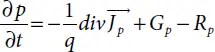
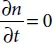 and
and 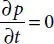 .
.