Stephen J. Mildenhall - Pricing Insurance Risk

If you’re returning from a business trip you are much more concerned about wasting time—your company will pay for flight changes, and there’s a flight every hour. You use a similar approach to a pricing risk measure. You consider the average journey times you have experienced, factoring in the time of day, day of the week, and weather, and add a small margin for minor traffic issues.

Example 35Stress tests are often used as a risk measure: what are my results in a stressed environment? Again, there are capital and pricing flavors. Lloyd’s Realistic Disaster Scenarios, Example 3.4.4, define a capital stress test. They quantify the impact of extreme but realistic events. By ensuring adequate capital to pay all claims from RDS events, Lloyd’s can communicate its risk paying capacity to a nontechnical audience. Setting capital using a risk measure equal to the worst outcome over the RDS set achieves this goal. Insurers can use alternative climate scenarios in catastrophe models to stress test pricing. These act to increase mean event frequency. An insurer may want to price with a margin reflecting the uncertainty in expected mean frequency. Here, the stress test applies to pricing.

What functional forms should we consider for a risk measure? The representation of ρ(X) should be related to the potential outcomes described by X . The most basic summarization of X is the mean, which is the probability weighted sum of outcomes

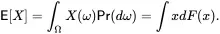(3.15)

There are many different ways we could generalize the mean; see Figure 3.14.

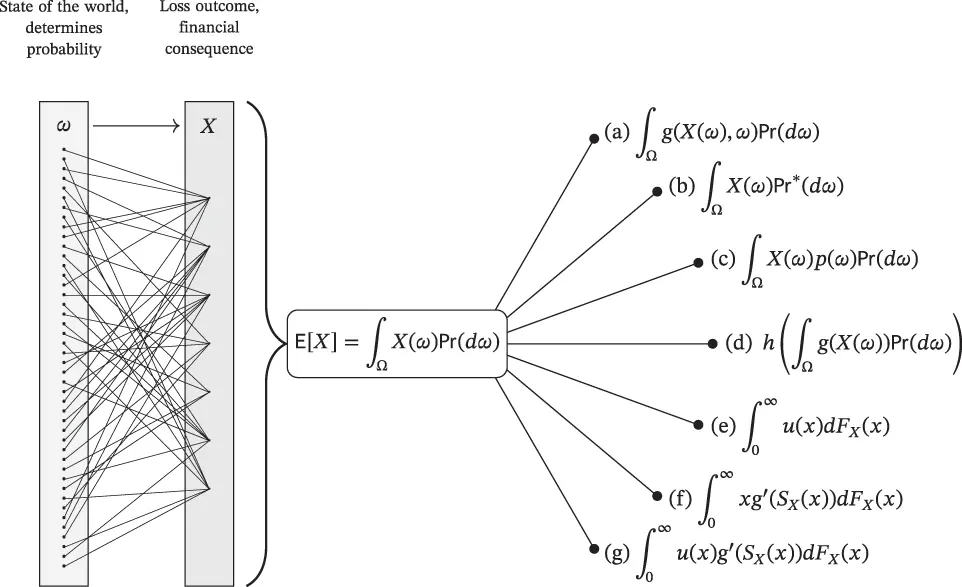
Figure 3.14 Potential functional forms for risk measures inspired by the expected value. The left shows the stochastic model, with many different states of the world mapping to the same loss outcome. These extensions overlap: a given risk measure can often be written in multiple ways.

1 Adjust outcomes by a factor depending on the outcome value and the explicit sample point ω. In finance the sample point is often called the state of the world or simply the state.

2 Adjust the probabilities to create a new measure. The new measure can make previously impossible events possible and vice versa.

3 Scale existing probabilities to create a new measure using a function of the explicit sample point (i.e. a random variable) p with p(ω)≥0 and E[p]=1. A specific scenario has this form. In this case events which are impossible under the original probability remain impossible. This approach is developed in Section 8.6.

4 Adjust with a function of loss and not ω. Standard deviation has this form, h(x)=x and g(x)=(x−μ)2.

5 Adjust outcomes independently of ω and leave probability unchanged. If the function u is increasing and convex then this form is called an expected utility risk measure. When outcomes can take positive and negative values we can adjust them with an S-shaped value function (Kahneman and Tversky 1979). The value function reflects attitudes to changes in wealth rather than final wealth.

6 Adjust probabilities by a function of the rank of the loss, but leaves the loss amount unchanged. This form is called dual utility theory and leads to spectral risk measures; see Section 10.7. (The function g:[0,1]→[0,1] must satisfy g(0)=0 and g(1)=1. It is used to adjust probabilities. Integration by parts shows that ∫0∞xg′(S(x))dF(x)=∫0∞g(S(x))dx since d(g(S(x)))/dx=−g′(S(x))dF/dx. S(x) is the rank of x.)

7 A combination of (e) and (f) leads to rank-dependent utility (Machina, Teugels and Sundt 2004; Quiggin 2012). Other attempts to adjust probabilities independent of ω are hard and often lead to measures that do not uniformly prefer more of a good to less, counter to any intuitive notion of behavior (Quiggin (2012); Section 4.8).

Adjusting probabilities rather than outcomes retains the original units of X , which is desirable for applications.

In methods (e)–(g), the result depends only on the distribution of X , not its value on each ω . Risk measures with this property are called law invariant; see Section 5.2.13. Most of the risk measures studied in detail in this book are law invariant.

Having created a risk measure, we can apply another function to the result. For example, we can load for operational and unmodeled risk by increasing the result by a fixed percentage.

We can create several different risk measures using a variety of techniques and then compute their weighted average, or their maximum. We can further adjust according to our belief in each. Using these processes allows us to create what appears to be a bewildering array of risk measures (Section 6.5); we are likely to confuse our clients—and ourselves. We say appears because, under the skin, there are far fewer than the table suggests. The situation is analogous to zoology; the number of individual species in the zoo is daunting, but a visit to the natural history museum reveals underlying similarities under the skin. In our case, the powerful classification theorem for coherent risk measures in Section 5.4 provides the skeleton. This controls the complexity and guides our selection.

Ultimately, the choice of risk measure must be appropriate for its intended application. More advice is given in Chapter 6, and Section 11.5.

Exercise 36Your student actuary proposes a new adjustment

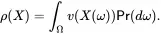
You tell them it is already in our list. Which item is it?

Exercise 37Which risk measure forms (a)–(g) address each of the following management, regulator, or investor concerns?

1 Insolvent is insolvent: I don’t care about the cause.

2 Differentiate a loss from a catastrophe peril from a loss from a noncatastrophe peril.

3 Incorporate different opinions about what is possible.

4 Avoid an outsize loss relative to peers.

5 Reflect ambiguity and estimation risk in probabilities. ◻

1 Define a risk and a financial risk.

2 Define and distinguish between timing and amount uncertainty, volume, and volatility, process risk and uncertainty, an insurance risk and a speculative risk, a diversifiable and nondiversifiable risk.

3 Define and give examples of systemic risks and distinguish them from systematic (nondiversifiable) risks.

4 Differentiate between objective and subjective probabilities.

5 Distinguish between process risk and uncertainty and parameter risk.

6 Define a catastrophe risk in an insurance context.

7 Define and identify the explicit, implicit, and dual implicit representations of risk.

8 Create a Lee diagram from a sample of losses or a loss distribution or a loss random variable.

9 Identify expected losses, excess losses, limited losses, put and call values, insurance charge and insurance savings, and policyholder deficit on a Lee diagram.

10 Compute expected losses, excess losses, limited losses, put and call values, insurance charge and insurance savings, and policyholder deficit given a distribution function.

11 Explain how put call parity is the same as insurance savings plus expense equals entry plus loss.

12 Explain and use different expressions for calculating the mean E[X].