Stephen J. Mildenhall - Pricing Insurance Risk

Example 32X⪰Y iff E[X]≤E[Y] defines a risk neutral preference. X⪰Y iff E[X]+SD(X)≤E[Y]+SD(Y) defines a mean-variance risk preference. Notice the order of the inequalities in both cases.

A risk measureis a numerical representations of risk preferences. If S and the preference ⪰ have certain additional properties then it is possible to find a risk measure ρ:S→R that representsit, in the sense that

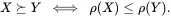(3.14)

The reversed inequality arises because ρ measures risk, and less risk is preferred to more.

The risk measure collapses a risk preference into a single number. It facilitates simple and consistent decision making. We consider risk measures and risk preferences in more detail in Section 5.

Exercise 33Based on your own views of risk, write down a few properties you believe a consistent risk preference should exhibit. For example, if you prefer X to Y what can you say about X + W vs. Y + W for another risk W ?

Risk measures quantify the following three characteristics of a risk random variable.

1 Volume: a smaller risk is preferred. The mean measures volume.

2 Volatility: a risk exhibiting less volatility (or variability) is preferred. Variance and standard deviation measure volatility. We use the word ‘volatility’ in a sense parallel to stock price volatility. Volatility is two-sided.

3 Tail: a risk with a lower likelihood of extreme outcomes is preferred. The level of loss with a 1% probability of exceedance is a tail risk measure. Tail risk is one-sided.

These characteristics overlap.

A risk measure must reflect volume because we want it to mirror a risk preference satisfying the MONO axiom, smaller risks are preferred to larger ones—even if the small risk is volatile and the large risk is certain. A measure of variability or tail risk that ignores volume is called a measure of deviation. The eponymous standard deviation is the, well, standard example. Adding the mean to a measure of deviation creates a risk measure.

Risk-based capital (RBC) formulas are risk measures. Many of them are volume based. They compute target capital by applying factors to premium, reserve, or asset balances. The factors vary according to the risk of each element. Examples include NAIC RBC, the Solvency II Solvency Capital Requirement standard formula, and most rating agency capital adequacy models. Classification rating plans are also risk measures. They compute a premium as a function of risk characteristics, such as building value and location, construction, occupancy, protection, and use for property insurance.

A risk measure sensitive to volatility quantifies mild to moderately adverse outcomes: outcomes frequent enough that most actuaries see examples during their careers. Management is often concerned with quarterly results volatility and can suppose investors are similarly troubled. Standard deviation quantifies volatility risk very well, and a two deviations from the mean rule of thumb turns out to be a surprisingly accurate estimate of a 20-year event in many situations.

Tail risk represents something so extreme it may or may not be experienced during a career, nevertheless it must always be considered possible. A tail risk catastrophe event often doubles or triples the previous worst historical event.

Variability and tail risk are distinct. An outcome of winning ¤1 million or ¤3 million has variability, but much less tail risk for most people than the possibility of gaining or losing ¤1 million. The variability of the two is the same but the tail risk is different. Risk is always relative to a base.

In Section 5.2 we enumerate several mathematical properties that risk measures should have, providing another way to characterize them.

Insurance company operations are governed by the interaction of two risk measures: a capital risk measure setting the needed amount of capital and a pricing risk measure determining its cost. These two roles should not be confused.

A capital risk measuredetermines the assets necessary to back an existing or hypothetical portfolio at a given level of confidence. This exercise is also reverse engineered: given existing or hypothetical assets, what are the constraints on business that can be written? Capital risk measures are used by management to determine economic capital, by a regulator to determine a minimum capital requirement, and by a rating agency to opine on the adequacy of held capital. Value at Risk (VaR) or Tail Value at Risk (TVaR) at some high confidence level, such as 99.5% or 1 in 200 years, are both popular, but other possible measures exist. These are both explored in Chapter 4.

A pricing risk measuredetermines the expected profit insureds need to pay in total to make it worthwhile for investors to bear the portfolio’s risk. Pricing risk measures are called premium calculation principles(PCP) in actuarial texts (Goovaerts, De Vylder and Haezendonck 1984). It is not expected that the loss be less than premium with a high degree of confidence—capital provides the cushion. But the premium must include a margin sufficient for the insurer to raise the needed capital cushion.

Risk measures typically have at a free parameter encoding their conservatism. As a result, there are two modes of use:

Given a level of conservatism, they determine a premium or capital requirement.

Given price or capital requirement, they evaluate its implied level of conservatism.

For example, a capital risk measure can be applied to capital model output to determine the amount of capital needed to be sufficient for 99% of outcomes. Or, it can evaluate what percentage of outcomes a given amount of capital covers.

By determinecapital or premium, we mean to derive a technical or benchmark quantity—usually the actual held capital or market premium differ. The benchmark value can be used to evaluate an actual one.

The capital and premium applications both determine a monetary quantity, so it is helpful if the risk measure is denominated in monetary units. The mean and standard deviation are monetary but variance or probability of default are not. If the risk measure is not monetary, then we need an undesirable extra step get to the answer.

In practice, the capital and pricing applications usually require different risk measures with different properties. Capital risk measures must be sensitive to tail risk to ensure solvency. Management, concerned with solvency and earnings risk, often looks for pricing risk measures that are sensitive to volatility. They can bemoan the fact that tail risk measures fail to see volatility risk, just as measures of height fail to quantify weight. As we discuss in Section 4.1, the solution is to use two risk measures. The interplay of the pricing and capital risk measures is a central theme of the book.

Example 34You have a flight to catch and want to allow sufficient time for your trip to the airport. George Stigler, a winner of the 1982 Nobel Prize in economics, said, “If you never miss the plane, you’re spending too much time in airports.” How much time do you allow?

If you’re going on vacation you are very concerned about missing your flight. You don’t want to lose any vacation time—there’s only one flight per day—and you’ll pay the cost of flight changes. You use a conservative capital risk measure approach. You build in a big time margin so that even in extreme traffic conditions you still make it to the airport on time.