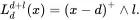Remark 20The relationships illustrated in Figure 3.3 are a discrete version of the formula for integration by parts. Consider approximating Riemann sums to the integral of the survival function. Let 0=x0
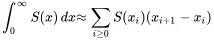 (3.2)
(3.2)
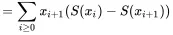 (3.3)
(3.3)
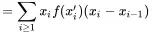 (3.4)
(3.4)
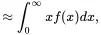 (3.5)
(3.5)
using Taylor’s theorem to write S(xi−1)−S(xi)=S(xi−(xi−xi−1))−S(xi)=−S′(xi′)(xi−xi−1)=f(xi′)(xi−xi−1), for some xi−1≤xi′≤xi.
Exercise 21Confirm the change in indexing between Eq. 3.2and Eq. 3.3is correct by looking at panels (d) and (e).
Technical Remark 22.In addition to the outcome-probability and survival function forms, there is a third, dual implicit outcome expression
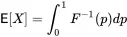
by change of variable substitution F(x)=p, f(x)dx=dp. This view replaces the probability defined by X with the uniform probability dp on [0,1].
Technical Remark 23.Figure 3.8 relates integral expressions for the mean and the different ways of representing risk presented in Section 3.4. When F is absolutely continuous it has a density, giving the usual ∫xf(x)dx representation of the mean in the second to last line.
 Figure 3.8 Different ways of computing the mean for a random variable
Figure 3.8 Different ways of computing the mean for a random variable
It is common to use limits and deductibles to transform the insured loss. If X is a loss random variable, then applying a deductible d transforms it into
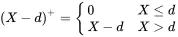
and applying a limitof l transforms it to
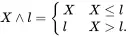
These notations are shorthand: for example, X∧l is the random variable with outcome (X∧l)(ω)=X(ω)∧l at sample point ω∈Ω.
When a policy has both a limit and a deductible, the limit is applied after the deductible. Applying a limit and a deductible creates what is called a limited excess of loss layeror simply a layer. Many reinsurance contracts and specialty lines policies are tranchedinto a coverage towerconsisting of multiple layers, written by multiple insurers. (A tranche means a piece cut off or a slice .) In this context, a layer is sometimes identified with its limit and the deductible is called the attachmentof the layer. A layer that attaches at 0 is called ground-up; all others are excess. Layers in a tower are typically arranged with no gaps.
Example 24An aggregate reinsurance tower to ¤100M could be structured as a ¤10M retention, layer 1: ¤10M excess 10M, layer 2: ¤30M excess 20M, and layer 3: ¤50M excess 50M. The cedent retains losses in excess of ¤100M. (Note: ¤30M excess 20M refers to a layer with a limit of ¤30M that attaches at ¤20M.)
Example 25Structured finance tranches asset-backed securities (MBS, CDO, etc.) in an analogous way. The tranches are generally determined to achieve a certain ratings defined by probability of default, meaning they have a dual implicit definition.
It is convenient to introduce the notation Ldd+l for the layer with limit l in excess of attachment d . The layer pays
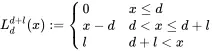 (3.6)
(3.6)
for a subject loss x . The detachmentor exhaustionpoint of the layer is d + l . The cover can be written succinctly as
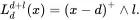
The notation Ldd+l mimics integrals, with the attachment and detachment points as sub- and super-scripts, and makes it easy to add them: L0l1+Ll1l1+l2=L0l1+l2.
We use the two equivalent expressions L0l(X) and X∧l interchangeably for a ground-up cover.
The expected loss and premium for a layer divided by the layer’s limit are called loss on lineand rate on line, respectively.
When applied to a random loss X , Ldd+l(X) becomes a random variable.
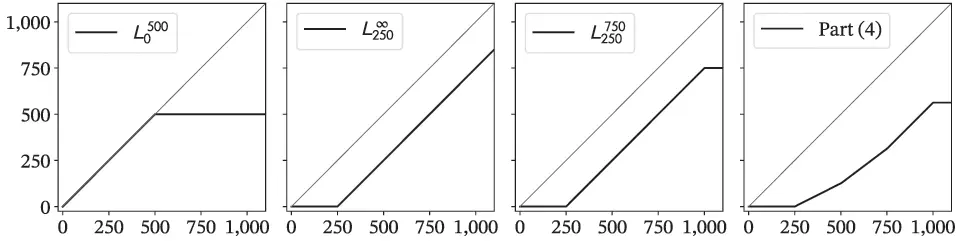
Exercise 26Using multiple layers it is possible to create any continuous indemnity function that increases with subject loss. Describe in words and plot payments from the following towers as functions of the subject loss 0≤x≤1000.
1 L0500(x)
2 L250∞(x)
3 L2501000(x)
4 0.5L250500(x)+0.75L500750+L7501000
5 Which of (1)–(4) has the same payouts as a call option? What is its strike?
6 Write the payout function for a put option in terms of L functions.
Solution.(1)–(4) See Figure 3.9. Cover (4) includes co-participations or coinsurance clauses, where some layers are only partially placed. (5) L250∞ has the same payout as a call option with strike 250. (6) A put option with strike k has payout function equal to k−L0k.
Figure 3.9 Sample layering functions for Exercise 26.
Remark 27Limits and deductibles can be applied per claimant, claim, occurrence, or in the aggregate. We assume the reader is familiar with these concepts. The exact meaning of a limit and deductible is defined by that of X . In this book X almost always represents aggregate loss on a portfolio.
3.5.4 Computing Layer Losses with the Lee Diagram
The Lee diagram makes it easy to visualize different loss layers and write down their expected values using survival-function form expectations. We use a for a height on the vertical axis because it usually represents assets available to Ins Co. for paying claims. Alternatively it can represent an attachment point.
Figure 3.10 illustrates several significant actuarial quantities in a Lee diagram.
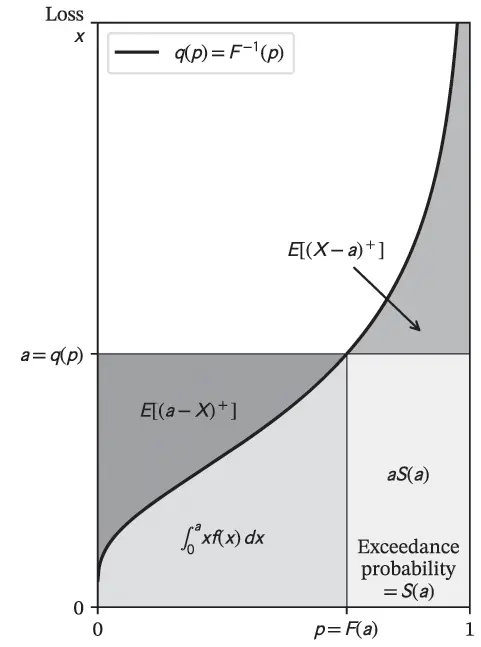
Figure 3.10 Insurance variables in a Lee diagram.
The area E[(X−a)+] equals the unconditional excess loss cost for losses in excess of the attachment a. It is called the insurance charge in US retrospective rating plans. When a represents assets it is called the insolvency put or expected policyholder deficit (EPD). In finance, the excess loss cost corresponds to the expected payout of a call option and a is called the strike price.
Читать дальше

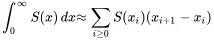 (3.2)
(3.2)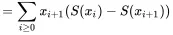 (3.3)
(3.3)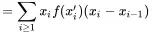 (3.4)
(3.4)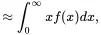 (3.5)
(3.5)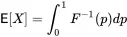
 Figure 3.8 Different ways of computing the mean for a random variable
Figure 3.8 Different ways of computing the mean for a random variable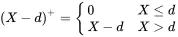
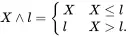
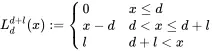 (3.6)
(3.6)