Маркус дю Сотой - О том, чего мы не можем знать. Путешествие к рубежам знаний

Затем, в районе V в. до н. э., положение дел начало изменяться, когда за эту тему взялись древние греки. В дополнение к алгоритмам стали появляться рассуждения, обосновывавшие, почему та или иная формула всегда работает, как указано на упаковке – или на глиняной табличке. Такое обоснование уже не сводилось к тому, что, раз алгоритм сработал последнюю тысячу раз, он, вероятно, будет работать и дальше: рассуждение объясняло, почему данное утверждение всегда будет справедливым. Так появилась идея доказательства.

Первым известным автором математического доказательства считается Фалес Милетский. Он доказал, что если взять любую точку на окружности и соединить ее с двумя концами диаметра этой окружности, то полученный угол всегда будет прямым. Какую бы окружность вы ни взяли, какую бы точку на ней ни выбрали, вы всегда получаете в точности прямой угол. Не приблизительно прямой, и не потому, что так, по-видимому, получается на всех ваших чертежах. Этот результат следует из свойств окружностей и прямых.

Доказательство Фалеса отталкивается от положений, в справедливости которых его читатель уже уверен и приходит к этому новому элементу знания, который вовсе не кажется изначально очевидным при простом взгляде на окружность, путем изобретательной последовательности логических ходов. Фокус заключается в построении отрезка, соединяющего исходную точку В, лежащую на окружности, с центром окружности О.

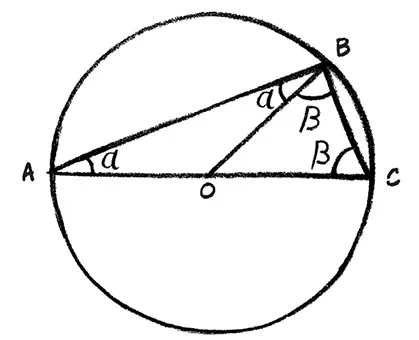
Какая нам от этого польза? Теперь у нас есть два треугольника, каждый из которых имеет две стороны равной длины. Это значит, что противоположные центру окружности углы в каждом из этих треугольников равны. Это свойство таких треугольников к тому времени уже было доказано. Возьмем большой треугольник АВС, который мы начертили в самом начале. Сумма его углов есть 2α + 2β. Тогда, с учетом того, что сумма всех углов треугольника должна быть равна 180°, мы знаем, что α + β = 90°, как и утверждал Фалес.

Когда я впервые увидел это доказательство в детстве, я пришел в настоящий восторг. Из картинки видно, что угол, примыкающий к окружности, похож на прямой. Но можно ли быть в этом уверенным? Мой разум искал какую-то причину, по которой это должно быть так. А потом, когда я перевернул страницу, увидел третий отрезок, который Фалес провел в центр окружности, и осознал логические следствия такого построения, я внезапно понял с ошеломляющей ясностью, почему этот угол действительно должен быть равен 90°.

Заметьте, что уже в этом доказательстве здание математического рассуждения строится на фундаменте положений, которые были доказаны ранее: например, того факта, что сумма углов треугольника всегда равна 180°. Открытие Фалеса, в свою очередь, стало основой для построения следующего этажа математического здания.

Доказательство Фалеса – лишь одно из многих, включенных в «Начала» Евклида. Многие считают эту книгу образцом самой сути математики и математического доказательства. Она начинается с основных структурных элементов, аксиом, геометрических утверждений, которые кажутся настолько самоочевидными, что читатель готов принять их в качестве надежного фундамента, на котором можно начать выстраивать логическое рассуждение.

Идея доказательства не возникла сама по себе, на пустом месте. Она скорее выросла из нового литературного стиля, разработанного в Древней Греции. Искусство риторики, сформулированное Аристотелем и подобными ему авторами, создало новый тип рассуждений, направленных на убеждение аудитории. Шла ли речь о юридических спорах, политических кампаниях или просто литературном повествовании, аудитории предлагалось совершить путешествие по логическому маршруту, в котором оратор пытался убедить слушателей в правоте своей позиции. Математика Египта и Вавилона выросла из строительства и измерения новых городов, возникавших в долинах Нила и Евфрата. Новая потребность в логике и риторических рассуждениях возникла из политических институтов эпохи расцвета греческих городов-государств, лежавших в основе греческой империи.

Для Аристотеля риторика была сочетанием чистой логики с методами, рассчитанными на воздействие на эмоции публики. Математическое доказательство происходит от первого из этих ингредиентов. Однако доказательство также связано с повествованием. И именно поэтому доказательство появилось в этот момент и в этом месте, вероятно, благодаря замысловатым историям, созданным такими драматургами, как Софокл и Еврипид, не в меньшей степени, чем благодаря философским диалогам Аристотеля и Платона.